Окружность, круг

Ребята, послушайте, какая тишина!
Это в школе начались уроки.
Мы не будем тратить время зря,
И приступим все к работе.

Загадки
Нет углов у меня,
И похож на блюдце я,
На тарелку и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья?
У круга есть одна подруга,
Знакома всем ее наружность!
Она идет по краю круга
И называется -…

- А я – окружность. Внутри меня есть точка непростая.
Зовется центром, от точек всех моих он равноудален.
- В каких же отношеньях ты с прямой? - Смотря с какой.
Внутри меня, ее отрезок хордою зовут.
Чем ближе к центру, тем она длинней.
- Что будет, если хорда через центр пройдет?
- О!!! Ее диаметром геометр назовет.
- А сколько у тебя диаметров? - Ох, много…
Их бесконечность, выражаясь строго.
При том, заметьте, что из них любой
Всегда есть радиус двойной. - А радиус?
- То всякая прямая, что к центру тянется, его соединяя
С любой из точек, мне принадлежащих,
Точнее, на окружности лежащих.

Из истории
Недаром древние греки считали окружность совершеннейшей и «самой круглой» фигурой. И в наши дни в некоторых ситуациях, когда хотят дать особую оценку, используют слово «круглый», которое считается синонимом слова «полнейший»

«Соберем» разбежавшиеся правила
Начало:
Окружность – замкнутая линия без самопересечений…
Круг – это часть плоскости,…
Радиус – это отрезок, соединяющий…
Диаметр – это отрезок, соединяющий…
Хорда - это отрезок, соединяющий…
Диаметр – это хорда,…
Конец:
…все точки которой находятся на одинаковом расстоянии от центра.
…ограниченная окружностью.
…две точки окружности.
…проходящая через центр.
…соединяющий центр окружности с любой точкой на окружности.
…две точки окружности и проходящий через центр.

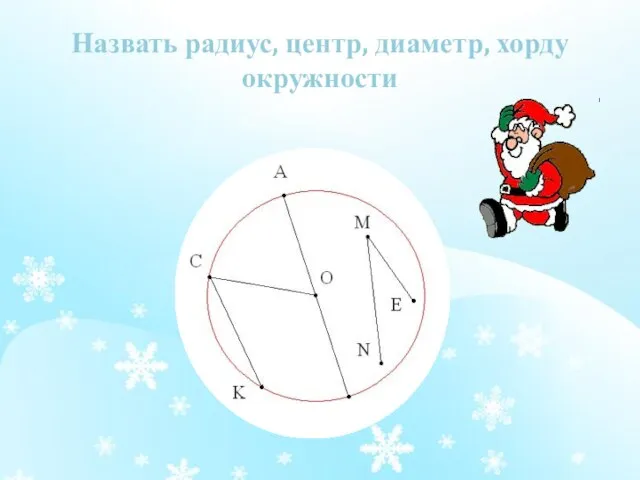
Назвать радиус, центр, диаметр, хорду окружности

Загадка
Танцевальное движенье
Совершеннейшей ноги
И круги, круги, круги
Вызывают восхищенье.
Балерина создавала
Точный круг в один момент,
Подивился ей немало
Достославный геометр.
О прекрасной балерине
Вспоминал частенько он
Не по этой ли причине
... был изобретён.

Диаметр и длина окружности
r – радиус, d – диаметр, тогда: d=2 r.
С = π d или С = 2πr , где d - диаметр окружности, а - радиус окружности

Практическая работа

Из истории
“Убей меня, но не тронь моих кругов” ( Архимед)
Двадцать две совы скучали
На больших сухих суках.
Двадцать две совы мечтали
О семи больших мышах,
О мышах довольно юрких
В аккуратных серых шкурках.
Слюнки капали с усов
У огромных серых сов.
22/7

Мнемонические правила
π = 3, 14159265358…
Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Надо только постараться
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.

Самостоятельная работа

Из истории
Неофициальный праздник «День числа Пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3.14, что соответствует приближённому значению числа π.
Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи», так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π.
Памятник числу «пи» на ступенях перед зданием Музея искусств в Сиэтле.

Домашнее задание
1. Вычислите длину окружности, если r =5см.
2. Вычислите длину окружности, если d = 100 м.
3. Ученики организовали соревнования по фигурному катанию на велосипедах. В этих соревнованиях нужно было проехать четыре круга по окружности радиусом 3 м. Какое расстояние проехали велосипедисты в этом виде фигурного катания?
Творческое задание: по возможности придумать стихотворную фразу для запоминания числа π.

Рефлексия
1. С какой геометрической фигурой мы познакомились?
2. Что надо знать, чтобы построить окружность?
3. С помощью какого инструмента мы ее строим?
4. Чему равно число π?
5. Что нового, интересного узнали?
6. Что понравилось?