Операции унифицированной технологии построения цифровых пространств знаний

Пространства знаний
Концептуальные пространства знаний – общие модели отражающие разнообразные представления о многообразиях знаний в предметных областях и средствах работы со знаниями.
Цифровые пространства знаний - информационные системы, содержащие в структурированном и связном виде знания предметных областей, поддерживающие процессы их приобретения и практического использования.
Абстрактные пространства знаний – формальные модели, позволяющие изучать свойства многообразий идеальных знаний с помощью математических инструментов.

ПРОБЛЕМАТИКА И ЦЕЛИ РАБОТЫ
ЦЕЛИ
1. Разработка унифицированного, универсального, теоретически обоснованного формализма абстрактного пространства знаний.
2. Построение языка и эффективной технологии построения моделей пространств знаний и их трансформации в программно реализуемые модели.
ФУНДАМЕНТАЛЬНАЯ ПРОБЛЕМА
Создание научных основ для современных моделей многообразий знаний исследование информационных технологий и методов работы со знаниями

АБСТРАКТНОЕ ПРОСТРАНСТВО ЗНАНИЙ

1. Множество объектов, представляющих отдельные абстрактные знания, бесконечное и вычислимое.
2. Абстрактным знаниям эффективно сопоставляются их структурные представления.
3. На множестве абстрактных знаний определяются разрешимые отношения, позволяющие оценивать сходство и различие структурных представлений знаний.
4. Операции над знаниями, а также процессы пространств знаний моделируются специальными классами вычислимых отображений (морфизмов) и процессов.
ОСНОВЫ ФОРМАЛИЗАЦИИ

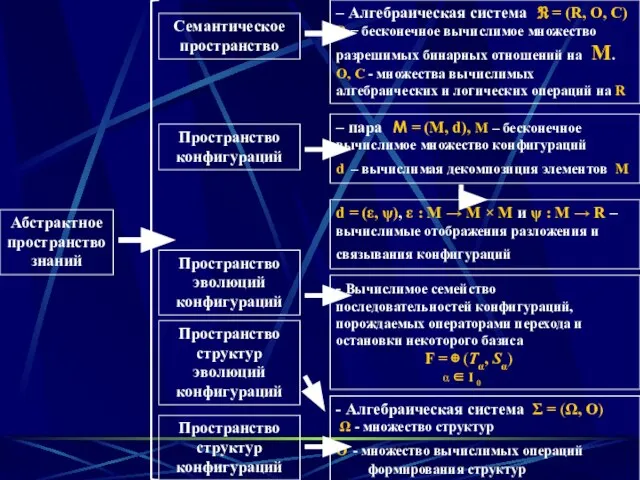
1. Семантическое пространство
Семантическое пространство - алгебраическая система
ℜ = (R , O , C) , где :
R − бесконечное вычислимое множество разрешимых
бинарных отношений на M , содержащее отношения
E = ∅ и T = R × R.
2. O − множество операций на, включающее объединение,
пересечение, обращение, произведение и композицию
3. С − множество логических операций, для которого отношение ρ 1 − вложения элементов R является разрешимым.
Пусть M - бесконечное вычислимое множество конфигураций, содержащее пустую конфигурацию Λ.

2. Пространства конфигураций
z
ε ,ψ
z 1
ψ(z)
ε : M → M ×M - декомпозиция
ψ : : M → R - связывание
Определение Декомпозицией конфигураций из M называется пара d = ( ε , ψ ), где ε и ψ являются отображениями разложения и связывания конфигураций.
Определение Пространством конфигураций называется
всякая пара М = (M , d), для которой
1. M – бесконечное вычислимое множество конфигураций;
2. d – декомпозиция элементов M.
z 2
ε (z) = (z1, z2)

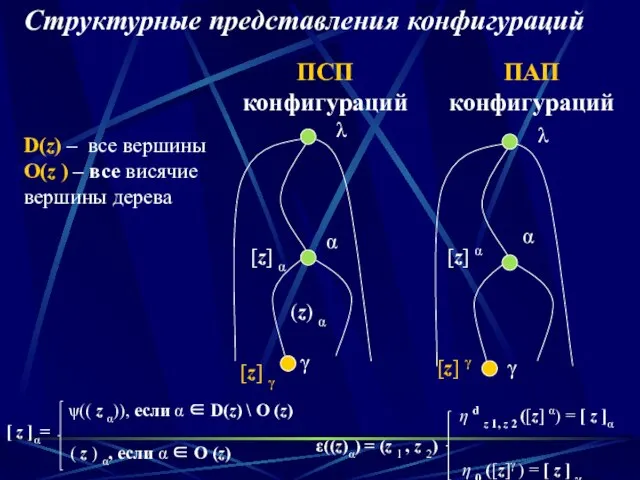
Структурные представления конфигураций
ε((z)α) = (z 1 , z 2)
ПСП конфигураций
ПАП конфигураций
α
(z) α
λ
λ
α
[z] α
D(z) – все вершины
O(z ) – все висячие вершины дерева
[z] γ
[z] γ
ψ(( z α)), если α ∈ D(z) \ O (z)
[ z ]α=
( z ) α, если α ∈ O (z)
[z] α
γ
γ
η d z 1, z 2 ([z] α) = [ z ]α
η 0 ([z]γ ) = [ z ] γ

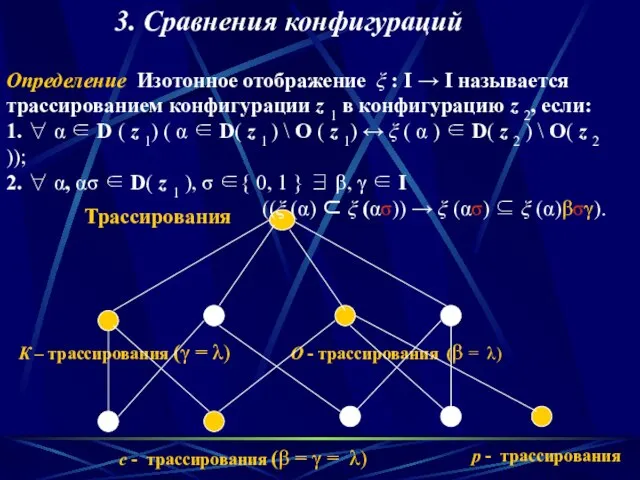
Трассирования
К – трассирования (γ = λ)
О - трассирования (β = λ)
с - трассирования (β = γ = λ)
р - трассирования
Определение Изотонное отображение ξ : I → I называется трассированием конфигурации z 1 в конфигурацию z 2, если:
1. ∀ α ∈ D ( z 1) ( α ∈ D( z 1 ) \ О ( z 1) ↔ ξ ( α ) ∈ D( z 2 ) \ О( z 2 ));
2. ∀ α, ασ ∈ D( z 1 ), σ ∈{ 0, 1 } ∃ β, γ ∈ I ((ξ (α) ⊂ ξ (ασ)) → ξ (ασ) ⊆ ξ (α)βσγ).
3. Сравнения конфигураций

Определение. Конфигурация z 1 I -трассируется в конфигурацию z 2 (z 1 ≤ I z 2, I ∈{ о, р, с, }), если существует такое I трассирование ξ : I → I, z 1 в z 2, что:
1. ∀ α ∈ O( z 1) (( z 1 ) α ρ 0 ( z 2 ) ξ (α) );
2. ∀ α ∈ D( z 1) \ O(z 1) ( [ z 1 ] α ρ 1 [z 2] ξ (α)).
Определение. Конфигурация z 1 I –вложена, I ∈{ о, р, с, к }, в конфигурацию z 2 ( z 1 ⊆ I z 2)), если
∃ z 1 ∈ Δ ( z 1), z 2 ∈ Δ ( z 2) ( z 1 ≤ I z 2).
Определение. Конфигурации z 1 и z 2 эквивалентные в отношении I - вложения, если z 1 ⊆ I z 2 и z 2 ⊆ I z 1.

Операции над формализованными знаниями моделируют универсальную систему этапов жизненных циклов знаний.
Универсальность системы операций для пространств знаний может рассматриваться в содержательном и точном смыслах. Во втором случае используются формальные критерии, позволяющие определять полную систему классов операций, согласованную с содержательными представлениями.
Одним из таких критериев является монотонность относительно трассирований или вложений.
4. Морфизмы пространств знаний
Основные форматы операций:
f : M * × M * → M *; f : M → M ; f : M → M * ; f : M * → R

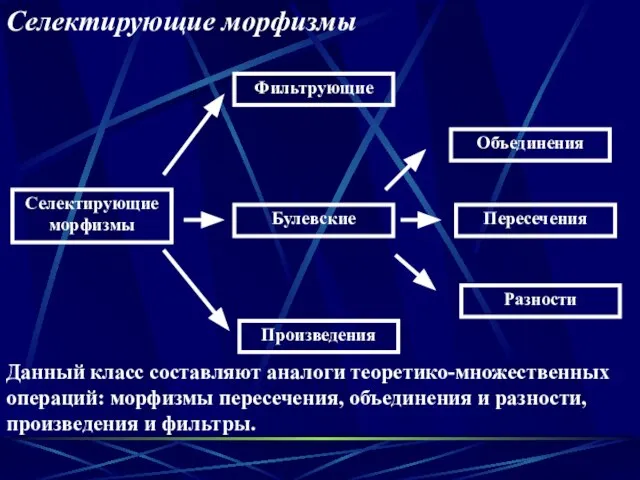
Селектирующие морфизмы
Фильтрующие
Булевские
Произведения
Разности
Пересечения
Объединения
Селектирующие морфизмы
Данный класс составляют аналоги теоретико-множественных операций: морфизмы пересечения, объединения и разности, произведения и фильтры.

1. Морфизм μ : M*×M* → M* называется пересечением , если
∀ V 1 , V 2 ∈ M* ∀ V ∈ M* (V ⊆ V 1 & V ⊆ V 2 → V ⊆ μ (V 1 , V 2 )).
2. Морфизм μ : M*×M* → M* называется объединением , если
V 1 , V 2 ∈ M* ∀ V ∈ M* ((V ⊆ V 1 ∨ V ⊆ V 2) → V ⊆ μ (V 1 , V 2 )).
3. Морфизм μ : M*×M fin → M* называется разностью , если
∀ V 1 , V 2 ∈ M*(μ (V 1, V 2) = { z | z ∈ M & {z} ⊆ V 1& {z} ⊄ V 2} )
Морфизм μ : M* → M* называется фильтром , если
∀ V 1, V 2∈ M*(μ (V 1∪ V 2) = μ (V 1)∪μ (V 2)) и ∀ V ∈ M*(μ (V)⊆V )
Морфизм μ : M* ×M* → M* называется произведением , если
V 1,V 2∈ M* ∀ z1 ∈ V 1, z2 ∈ V 2 ∃ z ∈ μ (V 1,V 2) (z1 ⊆ z & z2 ⊆ z );
V 1,V 2∈ M* ∃ z ∈ μ (V 1,V 2) ∃ z1 ∈ V 1, z2 ∈ V 2 (z1 ⊆ z & z2 ⊆ z )

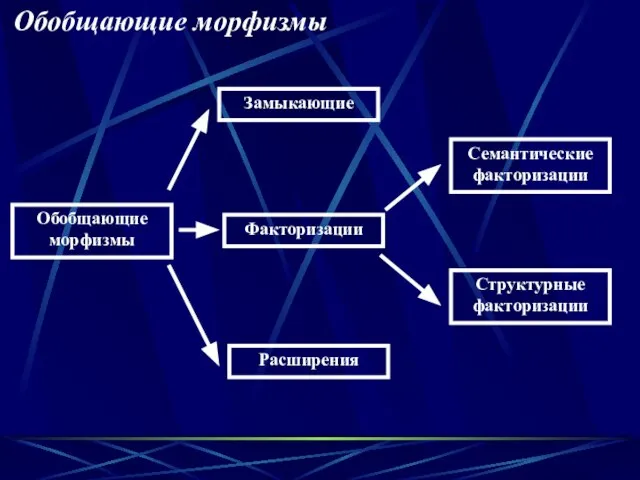
Обобщающие морфизмы
Замыкающие
Факторизации
Расширения
Структурные факторизации
Семантические факторизации
Обобщающие морфизмы

Морфизм μ : M* → M* называется факторизацией, если
V ∈ M* ∀ z ∈ V ∃ z1 ∈ μ (V ) (z = (z1)0) &
& ∀ z1 ∈ μ (V ) ∃ z ∈ V (z = (z1)0)
Морфизм μ : M* → M* называется замыкающим , если
∀ V ∈ M*(μ (V ) ⊆ [V] \ V )
Расширением V ∈ M* называется множество , образованное всеми такими конфигурациями, для которых существуют разбиения, составленные из конфигураций множества V.
Если V ∈ M*, то [V] – множество конфигураций, к которым сходятся вычислимые подмножества V

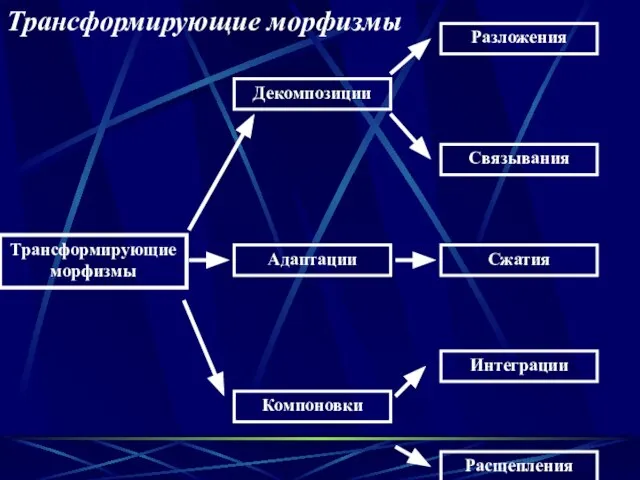
Трансформирующие морфизмы
Интеграции
Адаптации
Компоновки
Декомпозиции
Расщепления
Сжатия
Связывания
Разложения
Трансформирующие морфизмы

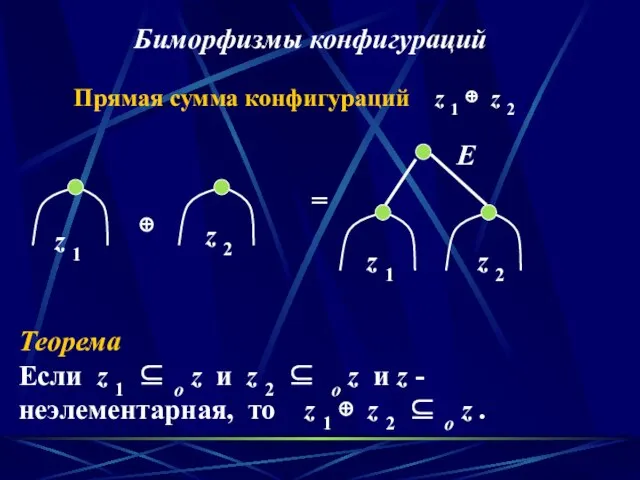
Прямая сумма конфигураций z 1 ⊕ z 2
Теорема
Если z 1 ⊆ о z и z 2 ⊆ о z и z - неэлементарная, то z 1 ⊕ z 2 ⊆ о z .
z 1
⊕
z 2
=
z 1
z 2
E
Биморфизмы конфигураций

Унифицирующие биморфизмы
Определение. Биморфизм μ называется унифицирующим, если: ∀ z 1, z 2 ∈ M (μ (z 1, z 2) ⊆ о z 1 & (μ (z 1, z 2) ⊆ о z 2)).
Отношение ≤ на множестве унифицирующих биморфизмов
∀μ 1, μ 2 (μ 1 ≤ μ 2 ↔ ∀ z 1, z 2 ∈ M (μ 1 (z 1, z 2) ⊆ о μ 2(z 1, z 2))).
Определим подкласс s – морфизмов.
отображения трассирования тождественные для внутренних вершин ПСП конфигураций.
z 1 ⊆ о z 2 ↔ z 1 ≤ о z 2.
Определение. Биморфизм μ : M 2 → M называется s – биморфизмом, если
∀ z 0 ∈ M (μ(z 0, z) и μ (z, z 0) - это s – морфизмы).
μSU – множество простых биморфизмов.
Теорема. μms является наибольшим элементом множества (μSU, ≤ s).

Τ р (z) , z ∈ M, - множество изотонных отображений соответствующих определению р – трассирования
R ξ (z), нагруженное бинарное дерево с вершинами создаваемое из вершин ПСП z области значений ξ .
Эндоморфизмы конфигураций
Теорема. Если ξ ∈ Τ р (z) транзитивное отображение, то R ξ (z) образует ПСП некоторой конфигурации.
Пусть ξ : I → I изотонное и выполняются условия
∀ α ∈ I (ξ(α) ∈ D(z))
Если {α i | i ∈ N & α 1 = λ & ∀ j (|α j + 1 |= |α j | + 1)} – бесконечная последовательность, то ∃ i (ξ(α i ) ∈ O(z) )
Определим множества:
R(ξ, z) = {α | ∃ β ∈ Q(ξ, z) (α = ξ(β))};
Q(ξ, z) = { α | ξ(α) ∈ D(z) & α = βσ & ξ(α) ∈ O(z) &
ξ(α) ∈ D(z) → ξ(β) ∈ D(z) \ O(z) }

Определение. Вычмслмое множество конфигураций ω = { z i }, i ∈ N, s-сходится к конфигурации z если:
1. ∀ i ∈ N ( z i ≤ о z );
2. ∀ z ′ ∈ M (∀ i ∈ N (z i ≤ о z ′) → z ≤ о z ′);
3. ∀ α ∈ O( z ) ( [ z ] α ∈ M (ω) ∪ { Λ });
4. ∀ α ∈ D( z ) \ O( z ) ( [ z ] α ∈ R ( ω ) ∪ { E }).
5. Топологические свойства пространств знаний
Теорема. Пусть ω 1 = { z 1i}, i ∈ N, и ω 2 = { z 2i}, i ∈ N, - это
s-сходящиеся вычислимые множества конфигураций.
Тогда вычислимые множество конфигураций ω 3 = ω 1 ∪ ω 2 также является сходящимся.
Следствие. Если непустое вычислимое множество M ′ ⊆ M имеет конечную верхнюю грань, то M ′ является
s-сходящимся.

6. Эволюции конфигураций
1. Предназначены для моделирования процессов и жизненных
циклов в пространствах знаний;
2. Отличаются от морфизмов зависимостью результатов от времени и порядка поступления начальных данных;
3. Выполняются в неограниченном дискретном времени;
4. Группируются в системы процессов с общими механизмами построения процессов и определения их значений.

F = { ( T α, S α )│α ∈ I 0}
T α - оператор перехода
S α - оператор остановки
T α (z i ⊕ z*j) = [z i + 1] α ,
S α (z i ⊕ z*j) ∈ {0, 1, ∅}, α ∈ I 0, i = 0, 1, . . .
3. Шаг процесса z i ⇒ z i + 1
1. Начальное данное процесса:
вычислимая последовательность
ω = (z* 0, t 0), . . . , (z* j , t j), . . .
2. Процесс для начального данного ω - последовательность пар W = (z 0, 0), . . . , (z i , i), . . .
4. Значение процесса W в компоненте α ∈ I 0
F α(W) = {((z i ) α, i) ⏐ S α (z i ⊕ z* j) = 0 },
где z* j - конфигурация в I 1 в момент i
λ
α ∈ I 0
I 0 – область
процесса
I 1 - область
начального
данного
0
1
Представления процессов и их значений

Универсальные пространства эволюций конфигураций
Теорема. Существует универсальное пространство эволюций конфигураций.
Определение. Пространство эволюций конфигураций с базисом Fu = ⊕(Tuα, Suα) называется универсальным, если
F = (T α, S α ) ∃ μ F ∈ Θ ∃ ξ ∈ Ξ ∀ ω ∈ Ω ∀ α ∈ I 0
( L (F α (ω)) = L (Fu (μ (ω)) ξ (α) ).
2. Ξ - множество всюду определённых вычислимых отображений ξ : I 0 → I 0.
Определение. Вычислимое отображение μ : Ω → Ω является морфизмом эволюций конфигураций, если
ω ′, ω ′′∈ Ω ∀ t (ω ′ | t = ω′′ → ∃ τ ( L(μ( ω ′′)) = L(μ( ω ′ | τ))).
1. Θ - множество всех морфизмов эволюций конфигураций.

Абстрактное пространство знаний
Семантическое пространство
Пространство конфигураций
Пространство эволюций конфигураций
Пространство структур эволюций конфигураций
Пространство структур конфигураций
– Алгебраическая система ℜ = (R, O, C)
R − бесконечное вычислимое множество разрешимых бинарных отношений на M.
O, C - множества вычислимых алгебраических и логических операций на R
- Вычислимое семейство последовательностей конфигураций, порождаемых операторами перехода и остановки некоторого базиса F = ⊕ (Tα, Sα)
α ∈ I 0
– пара М = (M, d), M – бесконечное вычислимое множество конфигураций
d – вычислимая декомпозиция элементов M
d = (ε, ψ), ε : M → M × M и ψ : M → R – вычислимые отображения разложения и связывания конфигураций
- Алгебраическая система Σ = (Ω, O)
Ω - множество структур
O - множество вычислимых операций формирования структур

a. Операции конструирования и трансформации моделей пространств знаний
b. Форматы описаний компонентов пространств знаний
Элементы языка моделирования пространств знаний KML
7. Язык и Технология пространств знаний

Операции конструирования и трансформации пространств знаний
Базовые операции на множестве формальных моделей:
1. Интеграция – расщепление
2 Гомоморфное расширение – гомоморфное вложение
Модели компонентов пространств знаний представляются формальными системами вида Σ = (T, F, P)
T, F, P - системы классов данных, морфизмов и предикатов структурированных отношениями вложения и агрегирования
Свойства классов представляются формализованными описаниями специальной структуры.

Унифицированная формальная модель
Формальная модель
Множество данных
Множество морфизмов
Множество предикатов
На множествах T, F и P определены вычислимые семейства классов CT, CF и CP, содержащих все элементы данных множеств. Такие семейства структурированы разрешимыми отношениями вложения и агрегирования классов, обозначаемыми в виде и .

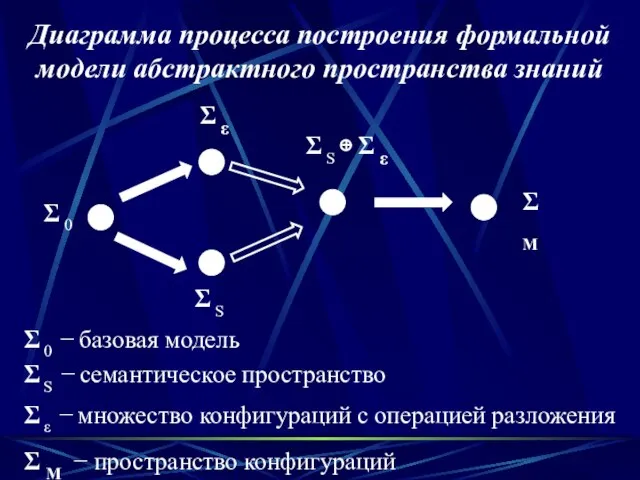
Диаграмма процесса построения формальной модели абстрактного пространства знаний
Σ 0
Σ S
Σ ε
Σ S ⊕ Σ ε
Σ M
Σ 0 − базовая модель
Σ S − семантическое пространство
Σ M − пространство конфигураций
Σ ε − множество конфигураций с операцией разложения

Гомоморфные вложения формальных моделей
f (x 1, . . . , x n )
ϕ (y 1, . . . , y m )
1. Соответствие классов (данных, морфизмов, предикатов)
2. Сохранение значений
hf f (x 1, . . . , x n ) = ϕ (ξ 1(x 1, . . . , x n ), . . . , ξ m (x 1, . . . , x n ) )
p (x 1, . . . , x n )
π (y 1, . . . , y m )
p (x 1, . . . , x n ) = π (η 1(x 1, . . . , x n ), . . . , η m (x 1, . . . , x n ) )

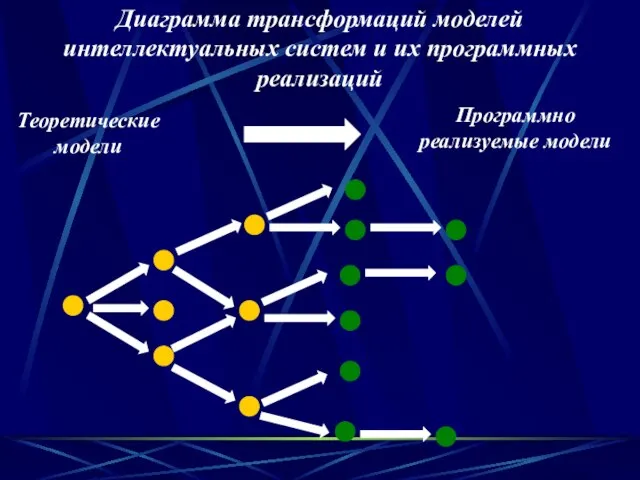
Программно реализуемые модели
Диаграмма трансформаций моделей интеллектуальных систем и их программных реализаций
Теоретические модели

Язык моделирования пространств знаний
KML

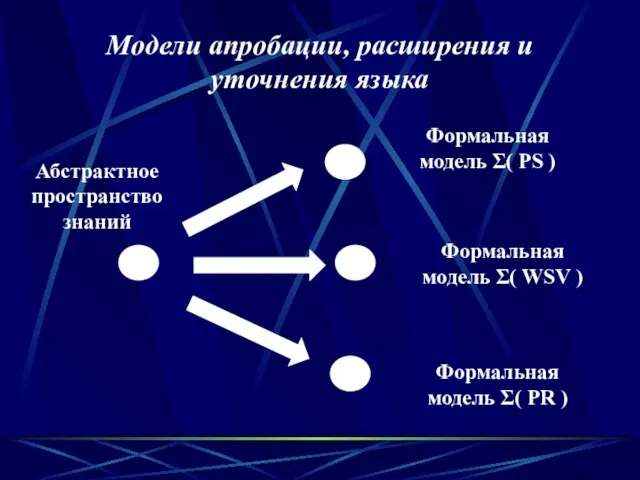
Модели апробации, расширения и уточнения языка
Абстрактное пространство знаний
Формальная модель Σ( PS )
Формальная модель Σ( WSV )
Формальная модель Σ( PR )

Диаграммы классов объектов абстрактного пространства знаний
1
2
3

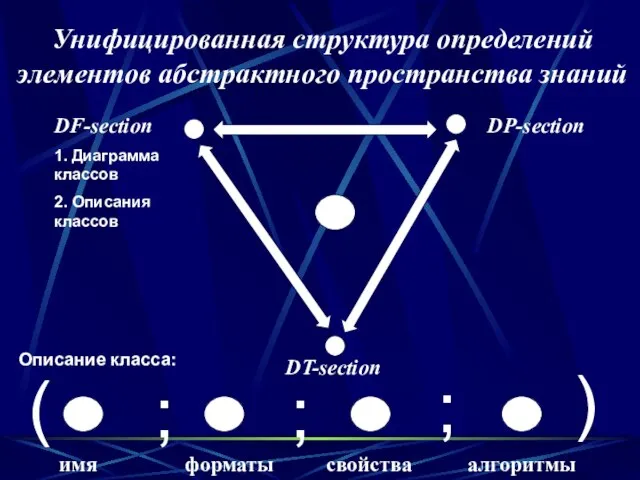
DT-section
DF-section
1. Диаграмма классов
2. Описания классов
DP-section
имя
форматы
свойства
алгоритмы
Унифицированная структура определений элементов абстрактного пространства знаний
Описание класса:
(
)
;
;
;

Примеры описаний классов
Класс данных Класс конфигураций
(M; {z i | i ∈ N}; Λ ∈ M; G(M), D(M)).
2. Класс данных Семантическое пространство}
(R;{r i | i ∈ N & r i ∈ (M × M)* }; E ∈ R, T ∈ R; G(R), D(R)).
3. Класс данных Семейство параметризованных классов вершин ПСП конфигураций}
(D(z); {α | z ∈M & α =λ ∨ α = βσ & β ∈ I & σ ∈{0,1} & ε((z) β ) ≠ (Λ, Λ) };
G(D(z) ), D(D(z))).
4. Класс морфизмов Каноническое разложение конфигураций
({ε}; ε: M→M × M; ε(Λ)= (Λ, Λ); G({ε}).
5. Класс морфизмов Каноническое семантическое связывание}
( {ψ}; ε: M→R; ∀ z ∈M (ε(z)= (z1, z2) & z1 ≠ Λ ∨ z2 ≠ Λ) → ε(z) ∈ ψ(z)),
∀ r ∈R ∀ z1, z2 ∈M ∃! z ∈M(ε(z)= (z1, z2) & ε(z) ∈ ψ(z)) ;G({ψ}).
6. Класс Предикатов Вложение двоичных наборов
({Incl}= {⊆}; ⊆(I, I); ∀ α , β ∈I(α ⊆ β → ∃ γ ∈I(β= α γ )); G({Incl}).
7. Класс предикатов Трассируемость конфигураций
({Tr};Tr(M, M); Tr(z1, z2 ) ↔ ∃ ξ ∈F Tr(∀ α ∈D(z1) \ O(z1) ([z1] α ρ 1[z2] ξ (α) )&
& ∀ α ∈O(z1)((z1) α) ρ 0[z2] ξ (α) ); G({Tr}).

Общая структура описаний
Section <имя раздела> begin
Subsection Basic begin
Subsection Basic end
Subsection Special begin
Subsection Special end
Subsection Universal begin
Subsection Universal end
Section <имя раздела > end
Разделы описаний:
Section DT – классы данных
Section DF – классы морфизмов
Section DP – классы предикатов

XML –структура пространства знаний (1)

XML –структура пространства знаний (2)

Элементы языка описания
компонентов цифрового пространства знаний
<Раздел> = "section" <Имя раздела> "begin"
{ <Определение класса> | <Подраздел> }
"section" <Имя раздела> "end" .
<Подраздел> = "subsection" <Имя подраздела> "begin"
{ <Определение класса> | <Подраздел> }
"subsection" <Имя подраздела> "end" .
<Определение класса> = <Идентификатор класса>
"{" <Описание класса> "}"
"("
[";"
] [";"
] [";"
] ")." .

Классы модели пространства знаний
= <Имя класса> { "=" <Имя класса> } .
<Имя класса> = ( <Имя> { "×" <Имя> } )
| <Имя с параметром>
| <Имя одноэлементного класса> .
< Имя > = <Слово> [ < Слово > | "*" | <Число> ] [ < Слово > | <Число> ] .
<Имя с параметром> = <Имя> "(" < Имя переменной> { "," < Имя переменной> } ")" .
<Имя одноэлементного класса> = "{" <Имя> "}" | "{" <Специальное имя> "}" .

Область форматов
<Формат множества> = <Формат множества_Перечисление>
| <Формат множества_Характеристический предикат> .
<Формат множества_ Перечисление> = "{" <Имя переменной> { (","<Имя переменной> ) | ",…" } "}" .
<Формат множества_ Характеристический предикат> =
"{" <Имя переменной> ( ":" | "|" ) <Формула> "}".
<Формат морфизма> = <Имя морфизма> ":" <Имя класса> { "×" <Имя класса> } "→ " <Имя класса> { "×" <Имя класса> } .
<Формат предиката> = <Имя предиката > "(" <Имя класса> { "," <Имя класса> } ")" .

Область имен формального определения класса
= <Имя класса> { "=" <Имя класса> } .
<Имя класса> = ( <Имя> { "×" <Имя> } )
| <Имя с параметром>
| <Имя одноэлементного класса> .
< Имя > = <Слово> [ < Слово > | "*" | <Число> ] [ < Слово > | <Число> ] .
<Имя с параметром> = <Имя> "(" < Имя переменной> { "," < Имя переменной> } ")" .
<Имя одноэлементного класса> = "{" <Имя> "}" | "{" <Специальное имя> "}" .