Определение квадратного уравнения. Неполные квадратные уравнения

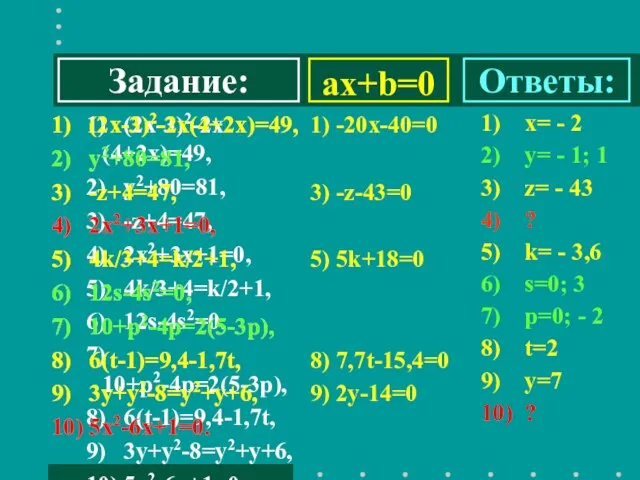
ax+b=0
1) (2х-3)2-2х(4+2х)=49,
2) y2+80=81,
3) -z+4=47,
4) 2x2+3х+1=0,
5) 4k/3+4=k/2+1,
6) 12s-4s2=0,
7) 10+p2-4p=2(5-3p),
8) 6(t-1)=9,4-1,7t,
9) 3y+y2-8=y2+y+6,
10) 5х2-6х+1=0.
1) -20х-40=0
3) -z-43=0
5) 5k+18=0
8) 7,7t-15,4=0
9) 2y-14=0
1) x= - 2
2) y= - 1; 1
3) z= - 43
4) ?
5) k= - 3,6
6) s=0; 3
7) p=0; - 2
8) t=2
9) y=7
10) ?
Задание:
Ответы:
1) (2х-3)2-2х(4+2х)=49,
2) y2+80=81,
3) -z+4=47,
4) 2x2+3х+1=0,
5) 4k/3+4=k/2+1,
6) 12s-4s2=0,
7) 10+p2-4p=2(5-3p),
8) 6(t-1)=9,4-1,7t,
9) 3y+y2-8=y2+y+6,
10) 5х2-6х+1=0.
1) (2х-3)2-2х(4+2х)=49,
2) y2+80=81,
3) -z+4=47,
4) 2x2+3х+1=0,
5) 4k/3+4=k/2+1,
6) 12s-4s2=0,
7) 10+p2-4p=2(5-3p),
8) 6(t-1)=9,4-1,7t,
9) 3y+y2-8=y2+y+6,
10) 5х2-6х+1=0.

1. Выучить определение квадратного уравнения.
2. Научиться определять по виду уравнения является ли оно квадратным или нет.
3. Научиться определять вид квадратного уравнения - полное оно или неполное.
4. Научиться выбирать нужный алгоритм решения неполного квадратного уравнения.
Ц е л и у р о к а :

1. Есть x2.
2. Есть х.
3. Есть число.
4. Есть нуль в правой части.
2x2 + 3х - 9 = 0, 5х2 - 6х + 1 = 0
2x2 + 3х - 9 = 0, 5х2 - 6х + 1 = 0
2x2 + 3х - 9 = 0, 5х2 - 6х + 1 = 0
2x2 + 3х - 9 = 0, 5х2 - 6х + 1 = 0
2x2 + 3х - 9 = 0, 5х2 - 6х + 1 = 0
x2 + х + = 0, х2 + х + = 0
a
a
c
c
b
b

1) 3,7х2-5х+1=0,
2) 48х2-х3-9=0,
3) 1-12х=0,
4) 2,1х2+2х-2/3=0,
5) 7/х2+3х-45=0,
6) х2-7х+√х=0,
7) 7х2-13=0,
8) х2√3+12х-1=0.
Задание:
Квадратные:
1) 3,7х2-5х+1=0,
4) 2,1х2+2х-2/3=0,
7) 7х2-13=0,
8) х2√3+12х-1=0.

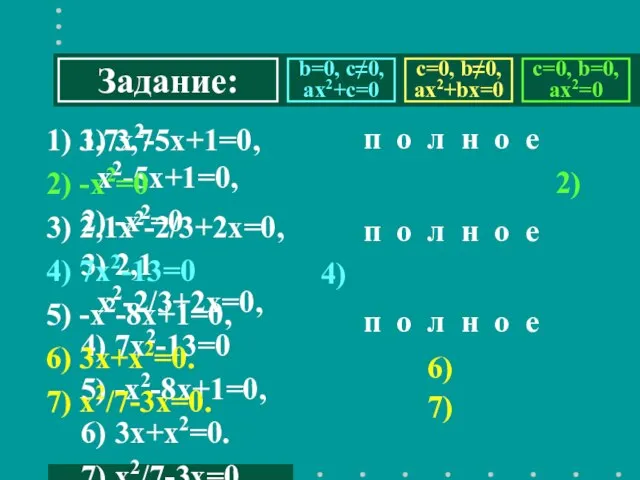
1) 3,7х2-5х+1=0,
2) -х2=0
3) 2,1х2-2/3+2х=0,
4) 7х2-13=0
5) х2√3+12х-1=0,
6) -10+3х+х2=0.
7) х2/7-3х=0.
1) a=3,7 b= -5 c=1
2) a= -1 b=0 c=0
3) a=2,1 b=2 c= -2/3
4) a=7 b=0 c= -13
5) a=√3 b=12 c= -1
6) a=1 b=3 c= -10
7) a=1/7 b= -3 c=0
Задание:
Ответы:
1) 3,7х2-5х+1=0,
2) -х2=0
3) 2,1х2-2/3+2х=0,
4) 7х2-13=0
5) х2√3+12х-1=0,
6) -10+3х+х2=0.
7) х2/7-3х=0.

1) 3,7х2-5х+1=0,
2) -х2=0
3) 2,1х2-2/3+2х=0,
4) 7х2-13=0
5) -х2-8х+1=0,
6) 3х+х2=0.
7) х2/7-3х=0.
b=0, c≠0, ax2+c=0
Задание:
c=0, b≠0, ax2+bx=0
c=0, b=0, ax2=0
2)
4)
7)
6)
1) 3,7х2-5х+1=0,
2) -х2=0
3) 2,1х2-2/3+2х=0,
4) 7х2-13=0
5) -х2-8х+1=0,
6) 3х+х2=0.
7) х2/7-3х=0.
п о л н о е
п о л н о е
п о л н о е

4x2-9=0
1) перенести свободный член в правую часть,
2) разделить обе части уравнения на а≠0,
3) если -с/а>0, то два корня:
х1=√-с/а и х2= -√-с/а; если -с/а<0, то корней нет.
4) записывается ответ
1) 4x2=9,
2) x2=9:4,
x2=2,25,
3) х1= √2,25,
х2= -√2,25,
х1=1,5,
х2=-1,5,
4) Ответ: х1=1,5,
х2=-1,5,
b=0, c≠0, ax2+c=0
6v2+24=0
1) 6v2=-24,
2) v2=-24:6,
v2=-4,
3) корней нет, т.к. -4<0
4) Ответ:
корней нет

3x2-4x=0
1) разложить левую часть на множители,
2) каждый множитель приравнивается к нулю,
3) решается каждое уравнение,
4) записывается ответ
1) х(3х-4)=0,
2) x=0 или
3х-4=0
3) х=0 или
3х=4,
х=4:3,
х=11/3,
4) Ответ: х1=0,
х2=11/3.
c=0, b≠0, ax2+bx=0
-5х2+6х=0
1) х(-5х+6)=0,
2) x=0 или
-5х+6=0
3) х=0 или
-5х=-6,
х= -6:(-5),
х=1,2
4) Ответ: х1=0,
х2=1,2.

-x2=0
1) разделим обе части на а≠0,
х2=0,
2) х=0,
3) записывается ответ.
1) x2=0,
2) x=0
3) Ответ: х=0.
c=0, b=0, ax2=0
9х2=0
1) x2=0,
2) x=0
3) Ответ: х=0.

1) 7х2-13=0,
2) 7k-14k2=0,
3) 12g2=0,
4) 5y2-4y=0,
5) 2h+h2=0,
6) 35-х2=0,
Задание:
Алгоритмы:
первый
второй
третий
второй
второй
первый
1) 7х2-13=0,
2) 7k-14k2=0,
3) 12g2=0,
4) 5y2-4y=0,
5) 2h+h2=0,
6) 35-х2=0,