Содержание
- 3. Тема 2.1. Оптические характеристики, используемые в фотонике и технологии оптических материалов для описания их свойств в
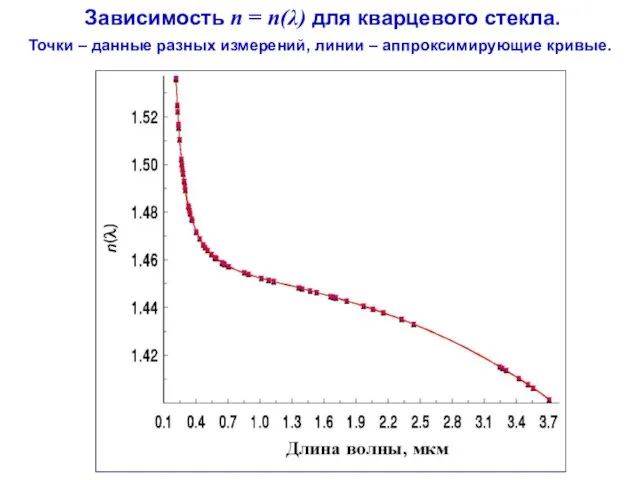
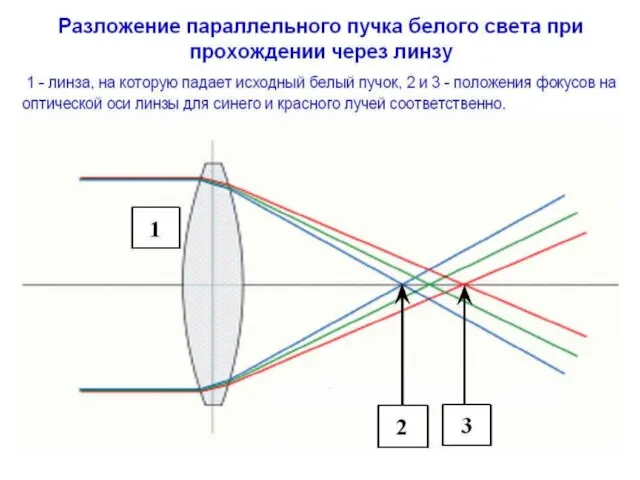
- 6. Зависимость n = n(λ) для кварцевого стекла. Точки – данные разных измерений, линии – аппроксимирующие кривые.
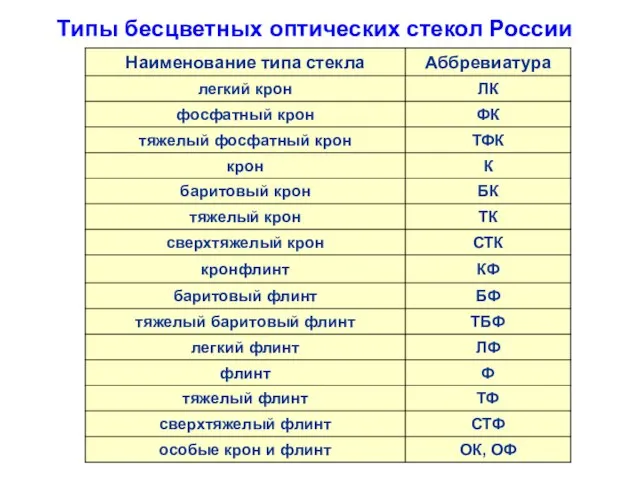
- 11. Типы бесцветных оптических стекол России
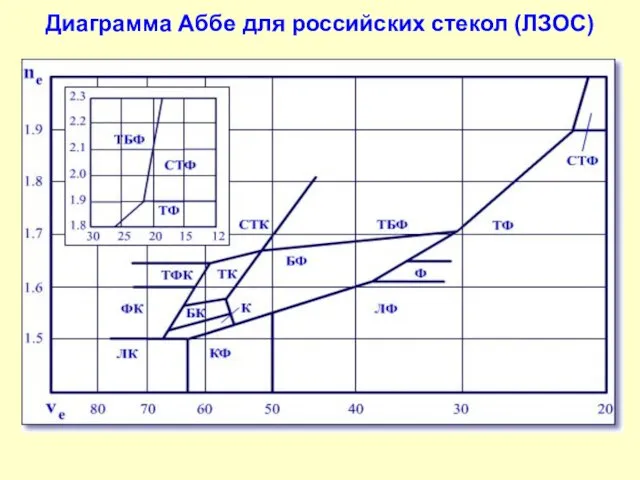
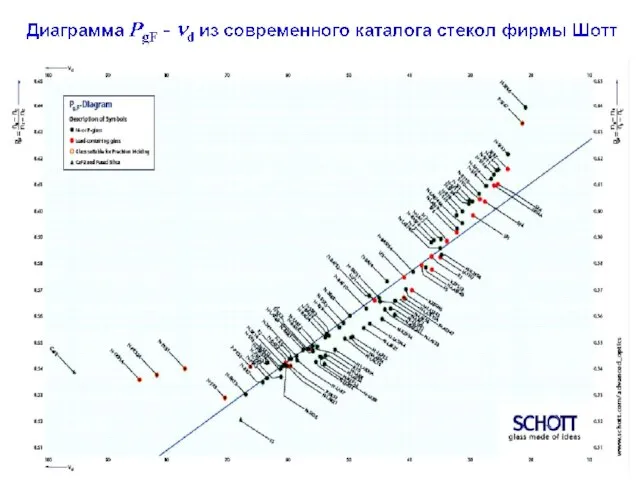
- 12. Диаграмма Аббе для российских стекол (ЛЗОС)
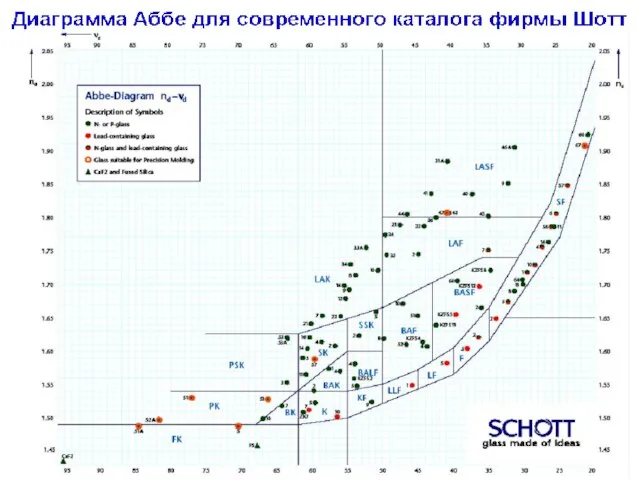
- 22. О вычислении отклонений оптических материалов от "нормальной" прямой "Нормальная" прямая на диаграмме "относительная частная дисперсия –
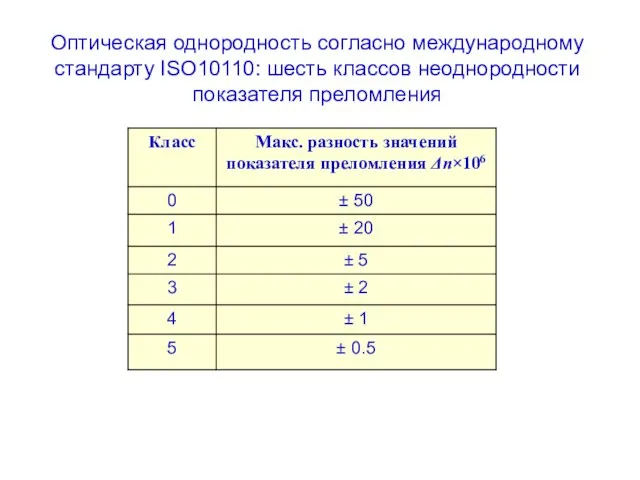
- 27. Оптическая однородность согласно международному стандарту ISO10110: шесть классов неоднородности показателя преломления
- 30. Тема 2.2. Основные закономерности физики оптических явлений в твердых телах и количественное описание дисперсии оптических постоянных
- 31. I. Основные понятия физики оптических явлений в твердых телах. I.1. Основные понятия и обшие соотношения. Отклик
- 32. I.1. Основные понятия и обшие соотношения (продолжение). Взаимосвязь между показателем преломления и диэлектрической проницае-мостью материала согласно
- 38. I.2. Процесс поглощения: основные черты. При поглощении кванта излучения электрон или атомная группа приобретает дополнительную энергию,
- 39. I.3. Виды и механизмы поглощения в твердых телах. А. Спектры электронных возбуждений или, кратко, электронные оптические
- 40. I.3. Виды и механизмы поглощения в твердых телах (продолжение) Б. Колебательные спектры. Они обусловлены переходами атомных
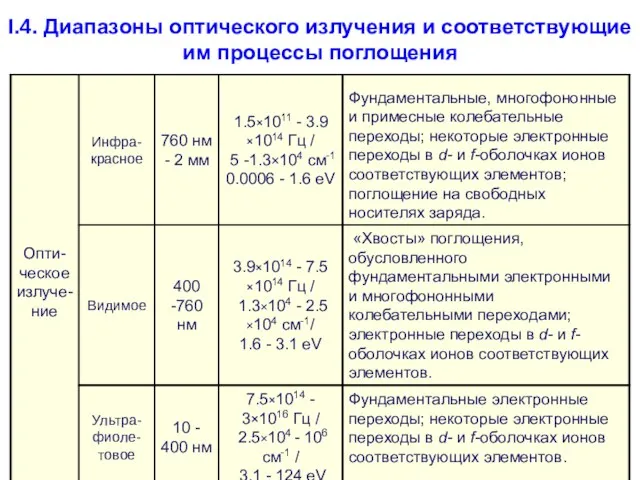
- 41. I.4. Диапазоны оптического излучения и соответствующие им процессы поглощения
- 42. I.5. Формирование электронных спектров твердого тела. I.5.1. Зонная схема в одноэлектронном приближении Это приближение удовлетворительно описывает
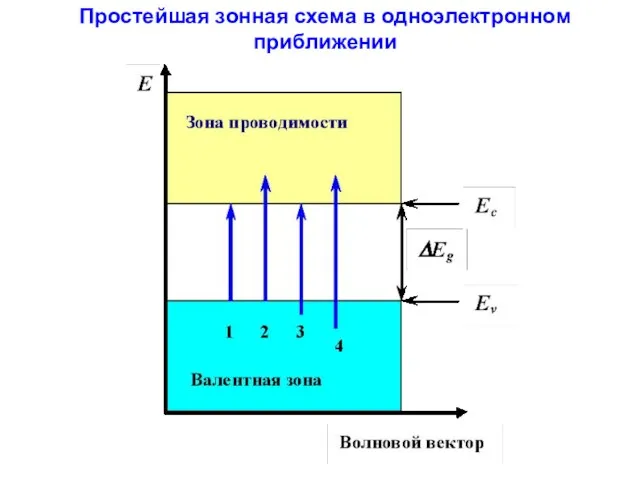
- 43. Простейшая зонная схема в одноэлектронном приближении
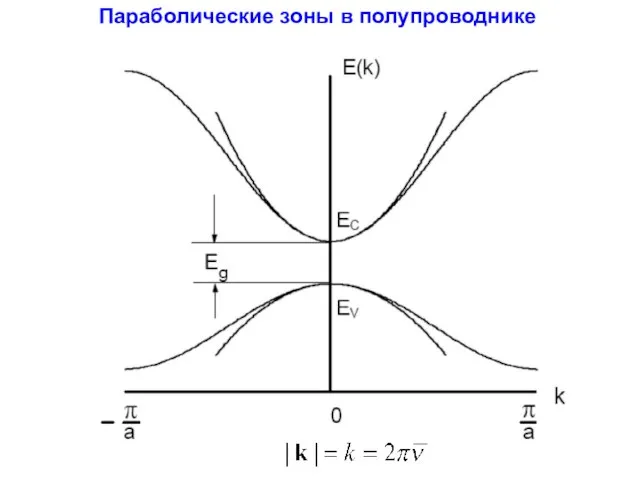
- 44. Параболические зоны в полупроводнике
- 45. I.5. Формирование электронных спектров твердого тела. I.5.1. Зонная схема в одноэлектронном приближении (продолжение) Основные положения: Между
- 46. I.5. Формирование электронных спектров твердого тела. I.5.2. Прямые и непрямые переходы в зонной схеме. Вышеописанные оптические
- 47. При наличии больших концентраций примесей или дефектов или при разупорядочении решетки границы валентной зоны и зоны
- 48. В отличие от ситуации, описываемой одноэлектронным приближением, взаимодействие электрона и дырки в материалах с большей шириной
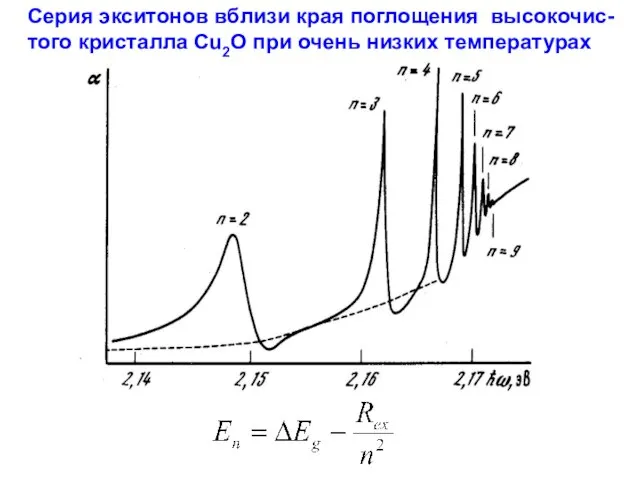
- 49. Серия экситонов вблизи края поглощения высокочис-того кристалла Cu2O при очень низких температурах
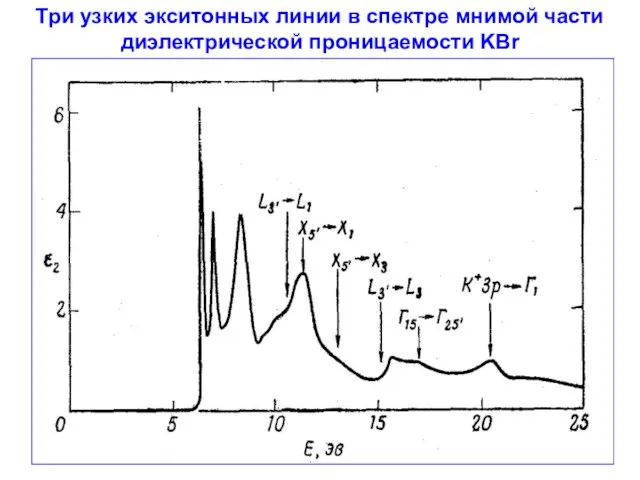
- 50. Три узких экситонных линии в спектре мнимой части диэлектрической проницаемости KBr
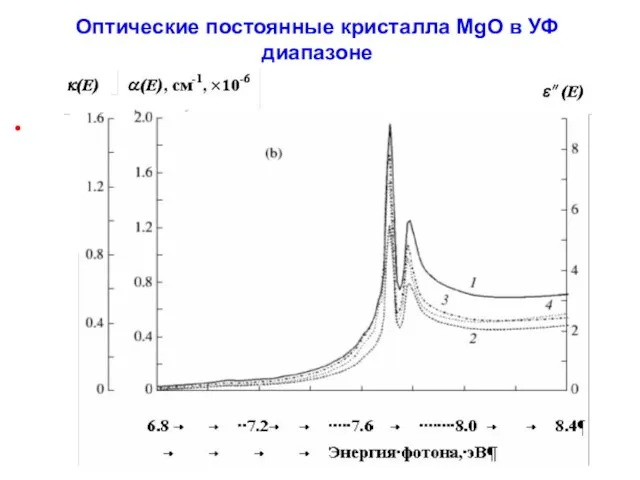
- 51. Оптические постоянные кристалла MgO в УФ диапазоне
- 52. I.5. Формирование электронных спектров твердого тела. I.5.5. Особенности электронных спектров диэлектриков. Вследствие низкой статической диэлектрической проницаемости
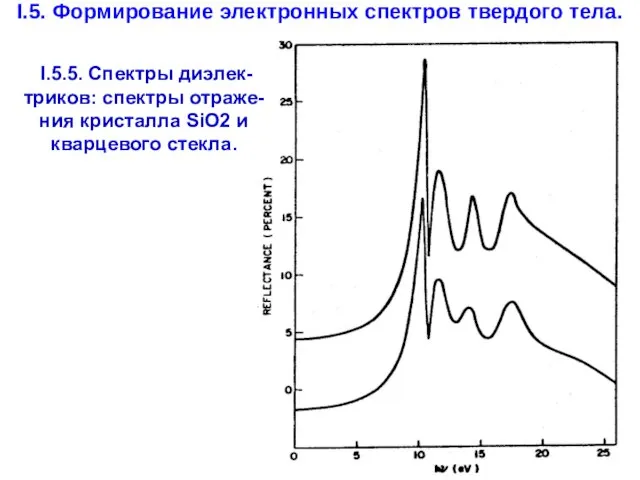
- 53. I.5. Формирование электронных спектров твердого тела. I.5.5. Спектры диэлек-триков: cпектры отраже-ния кристалла SiO2 и кварцевого стекла.
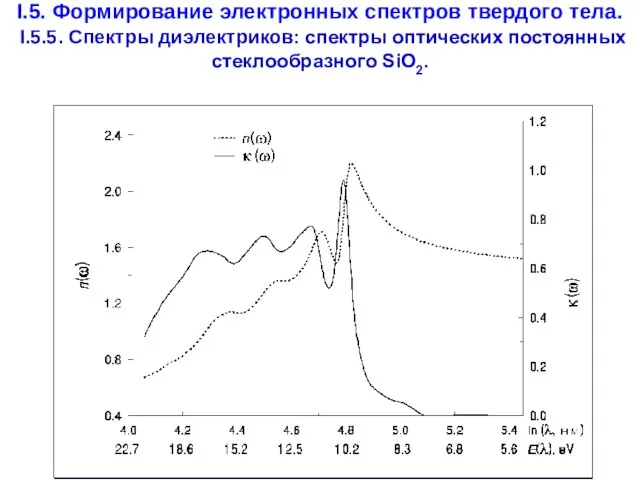
- 54. I.5. Формирование электронных спектров твердого тела. I.5.5. Спектры диэлектриков: cпектры оптических постоянных стеклообразного SiO2.
- 55. Установлено, что край собственного поглощения кремнезема в УФ диапазоне задается длинноволновым крылом экситонного максимума с центром
- 56. I.6. Формирование колебательных спектров твердого тела. I.6.1. Фундаментальные колебательные спектры. Простейшим вариантом вибратора (атомной системы, способной
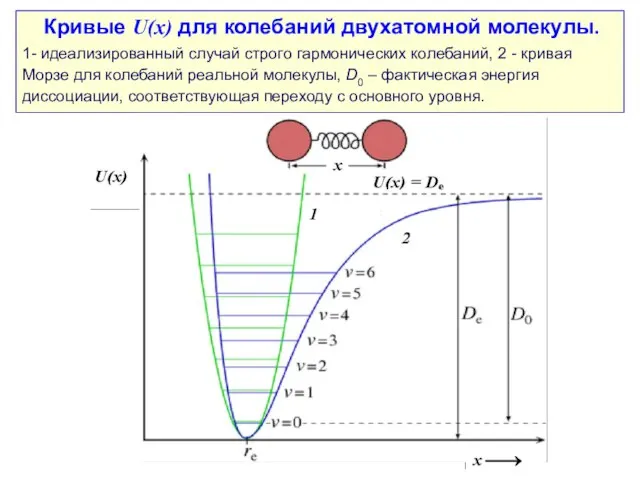
- 57. Кривые U(x) для колебаний двухатомной молекулы. 1- идеализированный случай строго гармонических колебаний, 2 - кривая Морзе
- 58. I.6.1. Фундаментальные колебательные спектры (случай твердых тел ). Колебательное возбуждение в твердом теле носит название “фонон”.
- 59. I.6.1. Фундаментальные спектры твердых тел (продолжение). Для трехмерной полимерной структуры кристалла картина существенно усложняется, так как
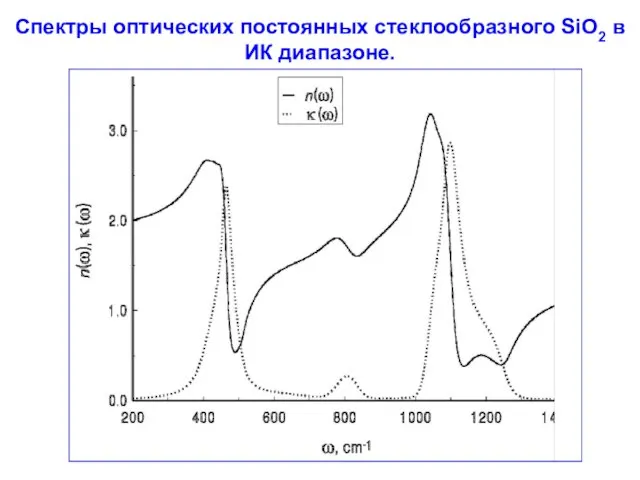
- 60. Спектры оптических постоянных стеклообразного SiO2 в ИК диапазоне. I
- 61. I.6.2. Многофононное поглощение. Поглощение ИК излучения может происходить, с некоторой достаточно малой вероятностью, и при частотах,
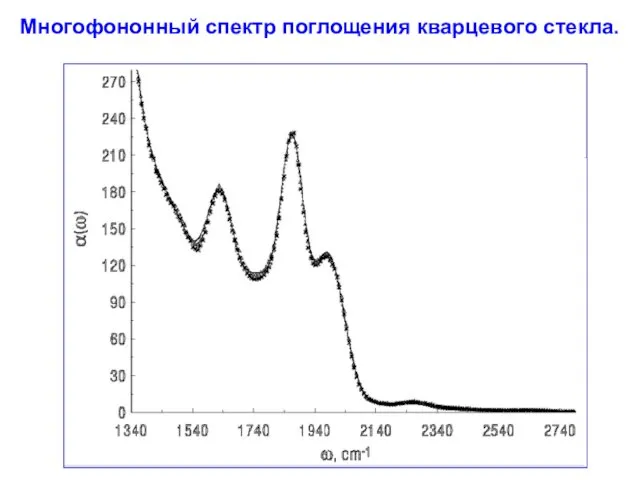
- 62. Многофононный спектр поглощения кварцевого стекла.
- 63. I.6.2. Многофононное поглощение (продолжение). Многофононное поглощение имеет важное значение для практического применения оптических материалов по следующим
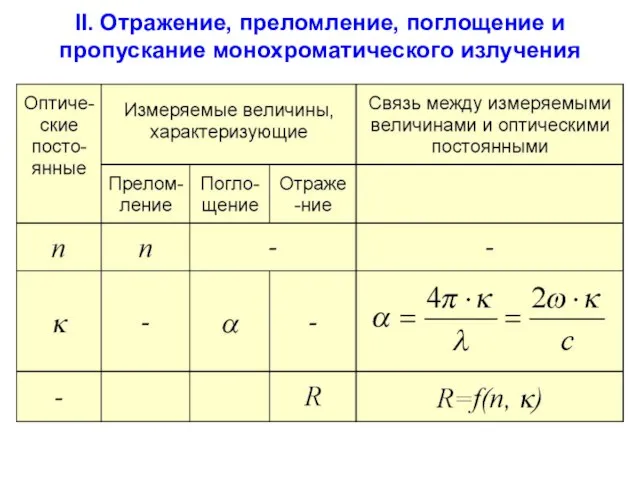
- 64. II. Отражение, преломление, поглощение и пропускание монохроматического излучения
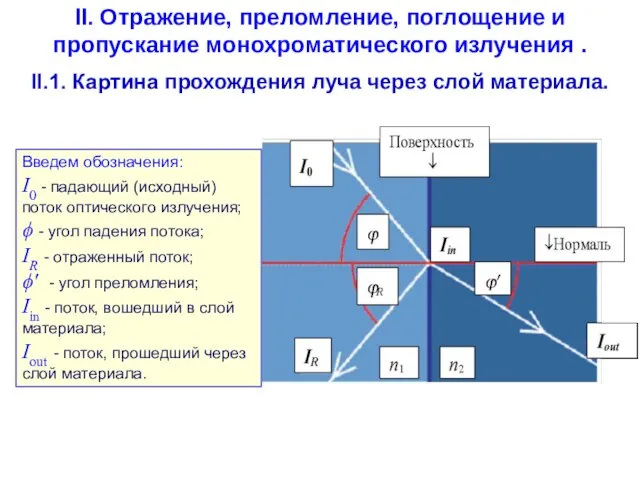
- 65. II. Отражение, преломление, поглощение и пропускание монохроматического излучения . II.1. Картина прохождения луча через слой материала.
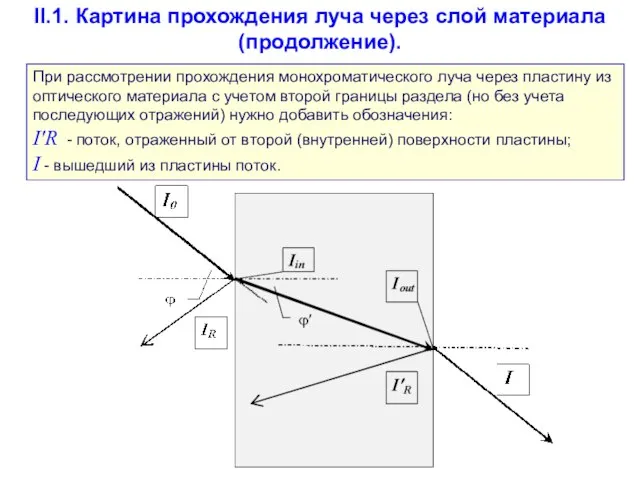
- 66. II.1. Картина прохождения луча через слой материала (продолжение). При рассмотрении прохождения монохроматического луча через пластину из
- 67. II.2. Характеристики прохождения луча через слой материала. Характеристикой материала является энергетический коэффициент внешнего отражения R =
- 68. II.3. Отражение на границах раздела оптических сред. II.3.1. Отражение на границе раздела двух прозрачных сред. Для
- 69. I.3. Отражение на границах раздела оптических сред. II.3.1. Отражение на границе раздела двух прозрачных сред (продолжение).
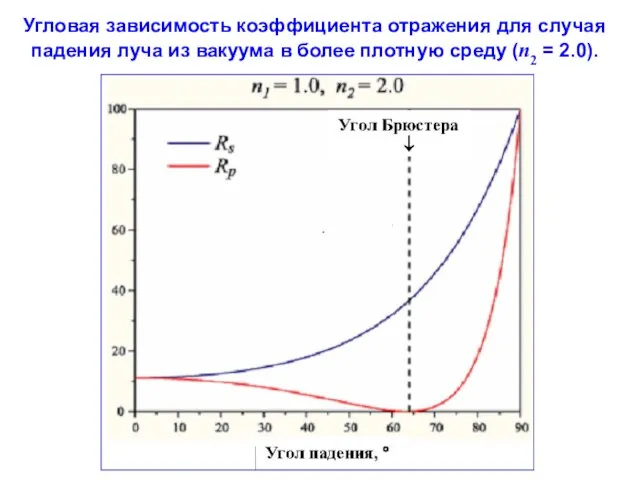
- 70. II.3. Отражение на границах раздела оптических сред. II.3.2. Угловая зависимость коэффициента отражения. При падении луча из
- 71. Угловая зависимость коэффициента отражения для случая падения луча из вакуума в более плотную среду (n2 =
- 72. II.3. Отражение на границах раздела оптических сред. II.3.2. Угловая зависимость коэффициента отражения (продолжение 1). При падении
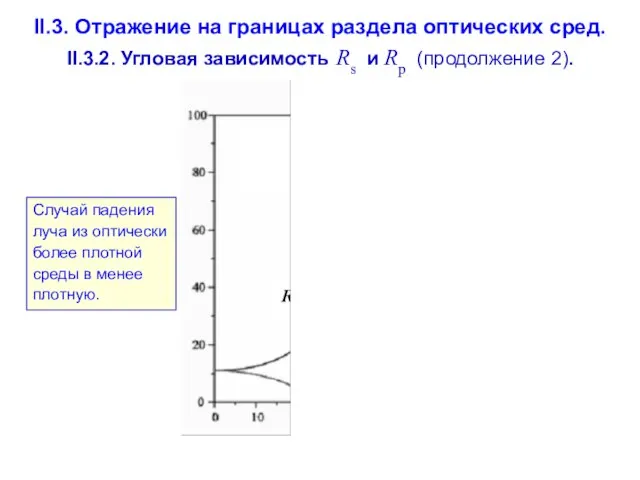
- 73. II.3. Отражение на границах раздела оптических сред. II.3.2. Угловая зависимость Rs и Rp (продолжение 2). Случай
- 74. II.3. Отражение на границах раздела оптических сред. II.3.3. Отражение на границе раздела с сильно поглощающей средой.
- 75. II.3. Отражение на границах раздела оптических сред. II.3.4. Фаза отраженного луча и амплитудный коэффициент отражения. Фаза
- 76. II.4. Поглощение излучения в материале. II.3.1. Закон Ламберта-Бугера. Закон Ламберта – Бугера, определяющий ослабление параллельного монохроматического
- 77. II.4. Поглощение излучения в материале. II.4.2. Закон Бера и его объединение с законом Ламберта-Бугера. Согласно найденному
- 78. II.4. Поглощение излучения в материале. II.4.3. Интенсивности потоков с учетом поглощения. Для пластины из поглощающего материала
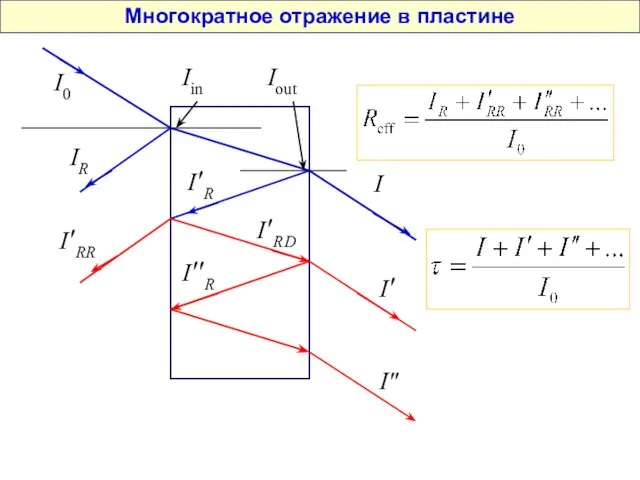
- 79. Многократное отражение в пластине I0 I Iin Iout IR I ′R I ′R D I ′′R
- 80. Результаты расчета коэффициента внешнего пропускания и коэффициента поглощения зависят от того, какое число последовательных отражений от
- 81. Значения коэффициентов поглощения рассчитываются из измеренных значений коэффициента пропускания τexp c учетом произвольного числа отражений m
- 82. III. Оптика материала в диапазоне прозрачности и его фундаментальные спектры поглощения: история. III.1. Феноменология. Оптические постоянные
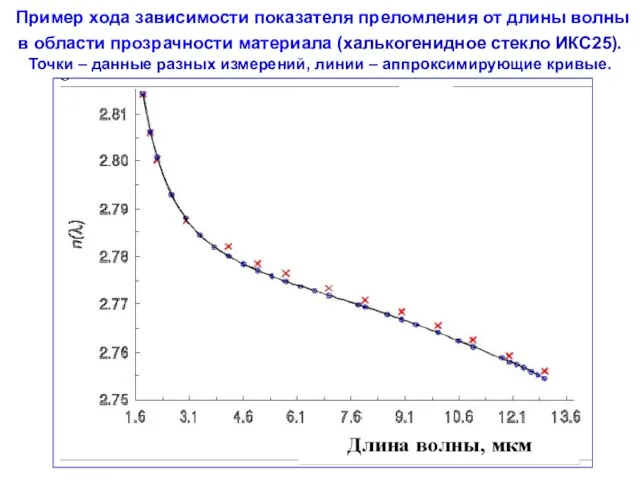
- 83. Пример хода зависимости показателя преломления от длины волны в области прозрачности материала (халькогенидное стекло ИКС25). Точки
- 84. III.1. Феноменология (продолжение). Картина дисперсии показателя преломления и показателя собственного поглощения в широком диапазоне длин волн,
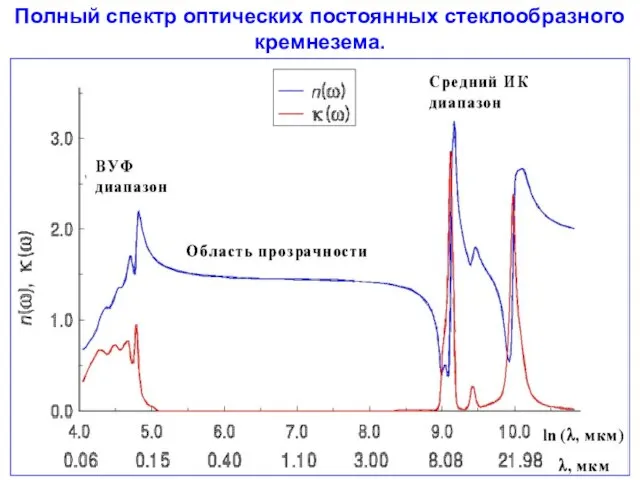
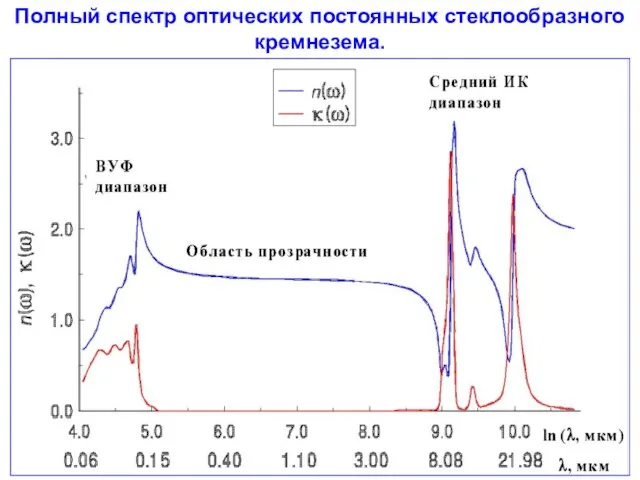
- 85. Полный спектр оптических постоянных стеклообразного кремнезема.
- 86. III.2. Соотношения Крамерса-Кронига. Наиболее общее описание внутренней взаимосвязи между оптическими постоянными в широком интервале частот дается
- 87. III.2. Соотношения Крамерса-Кронига (продолжение) Следует подчеркнуть, что интеграл во всех соотношениях Крамерса-Кронига – это так называемый
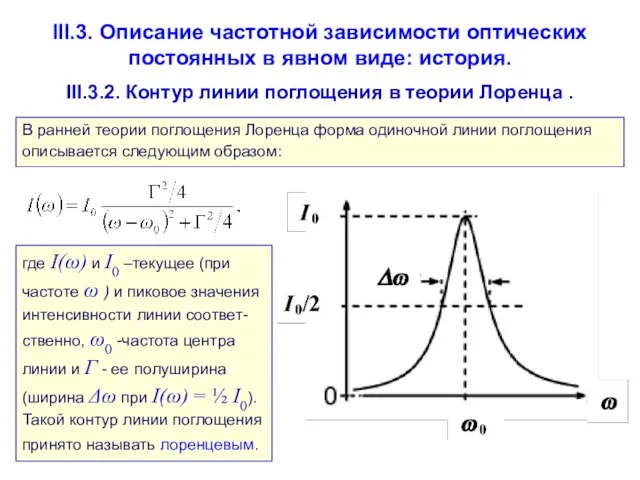
- 88. III.3. Описание частотной зависимости оптических постоянных в явном виде: история. III.3.1. Формула Зелльмейера. где n(λ) -
- 89. III.3. Описание частотной зависимости оптических постоянных в явном виде: история. III.3.2. Контур линии поглощения в теории
- 90. IV. Классическая теория дисперсии (L. Lorenz, 1829–1891, H. Lorentz, 1853–1928, P. Drude, 1863–1906) Исходная идея этой
- 91. IV.1. Исходные положения и модели теории дисперсии. IV.1.1. Частотная зависимость комплексной поляризуемости Комплексное смещение связанного электрона:
- 92. IV.1. Исходные положения и модели теории дисперсии. IV.1.2. Начальная версия модели Друде (модели дисперсии диэле-ктрической проницаемости
- 93. IV.1. Исходные положения и модели теории дисперсии. IV.1.3. Модель Лоренц-Лорентца (модель дисперсии диэлектрической проницаемости с учетом
- 94. IV.1. Исходные положения и модели теории дисперсии. IV.1.3. О модели Лоренц-Лорентца (продолжение). В течение длительного времени
- 95. IV.2. Классическая модель дисперсии диэлектрической проницаемости в современной науке. IV.2.1. Уточнение физического смысла величин, входящих в
- 96. IV.2. Классическая модель дисперсии диэлектрической проницаемости в современной науке. IV.2.1. Уточнение физического смысла величин, входящих в
- 97. IV.2. Классическая модель дисперсии диэлектрической проницаемости в современной науке. IV.2.2. Аппроксимация суммы вкладов наиболее высокочастотных осцилляторов
- 98. IV.2. Классическая модель дисперсии диэлектрической проницаемости в современной науке. IV.2.3. Более современный вид модели Друде. С
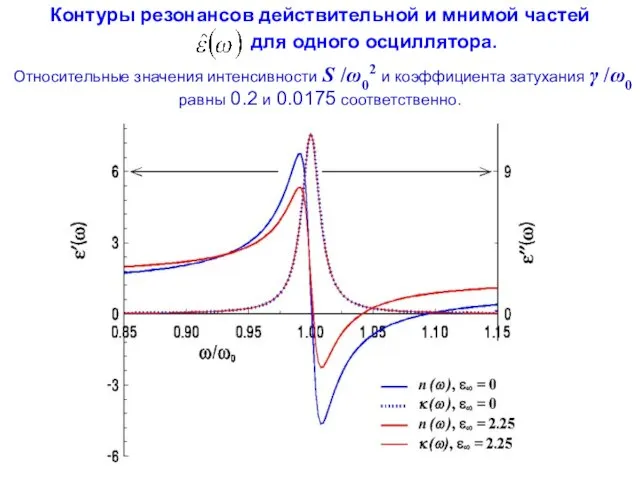
- 99. Контуры резонансов действительной и мнимой частей для одного осциллятора. Относительные значения интенсивности S /ω02 и коэффициента
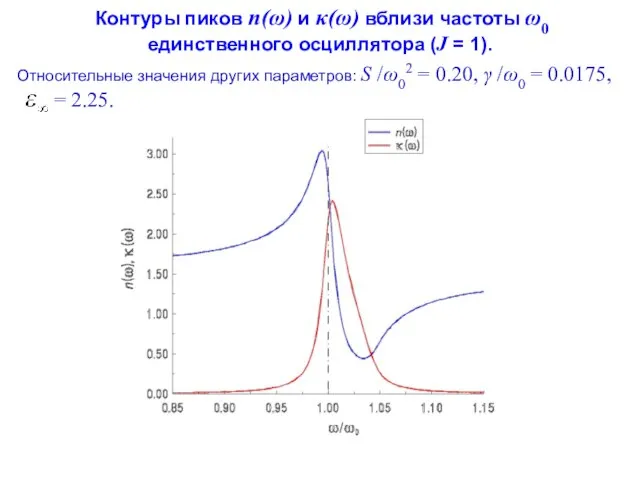
- 100. Контуры пиков n(ω) и κ(ω) вблизи частоты ω0 единственного осциллятора (J = 1). Относительные значения других
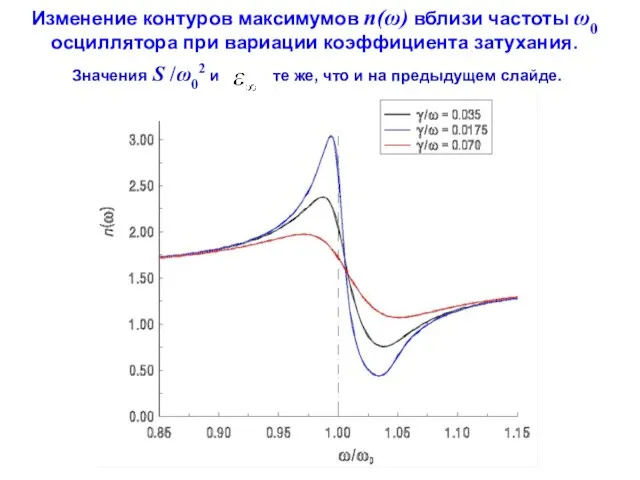
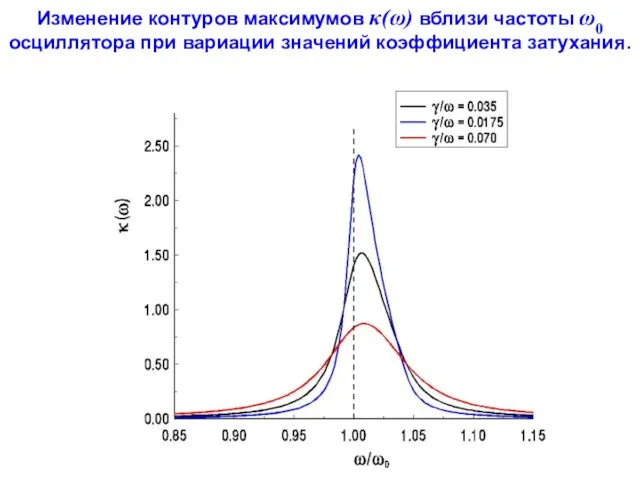
- 101. Изменение контуров максимумов n(ω) вблизи частоты ω0 осциллятора при вариации коэффициента затухания. Значения S /ω02 и
- 102. Изменение контуров максимумов κ(ω) вблизи частоты ω0 осциллятора при вариации значений коэффициента затухания.
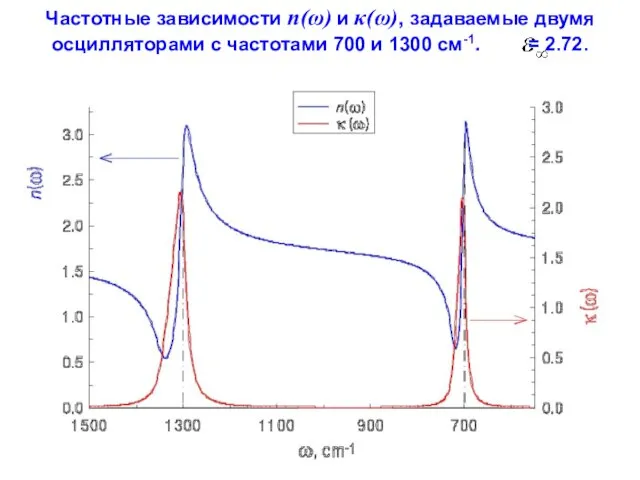
- 103. Частотные зависимости n(ω) и κ(ω), задаваемые двумя осцилляторами с частотами 700 и 1300 см-1. = 2.72.
- 104. Полный спектр оптических постоянных стеклообразного кремнезема.
- 105. Тема 2.3. Закономерности, определяющие специфику оптических свойств стекол, и количественное описание дисперсии их оптических постоянных
- 106. V. Влияние специфики структуры стекол на их оптические свойства. V.1. Неупорядоченность структуры как главная особенность стеклообразного
- 107. V.1. Неупорядоченность структуры как главная особенность стеклообразного состояния. V.1.1. Понятия ближнего, среднего и дальнего порядка. Шкала
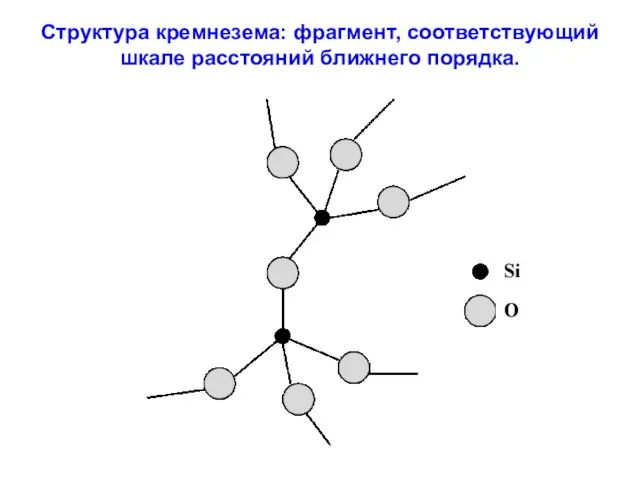
- 108. Структура кремнезема: фрагмент, соответствующий шкале расстояний ближнего порядка.
- 109. V.1. Неупорядоченность структуры как главная особенность стеклообразного состояния. V.1.3. Параметры ближнего порядка в кремнеземе. Ближний порядок
- 110. V.1. Неупорядоченность структуры как главная особенность стеклообразного состояния. V.1.3. Параметры ближнего порядка в кремнеземе (продолжение).
- 111. V.1. Неупорядоченность структуры как главная особенность стеклообразного состояния. V.1.4. Средний и дальний порядок в кремнеземе. В
- 112. V.2. Следствия неупорядоченности структуры для оптических свойств. V.2.1. Общие положения. Изложенная выше общая схема структуры стекла
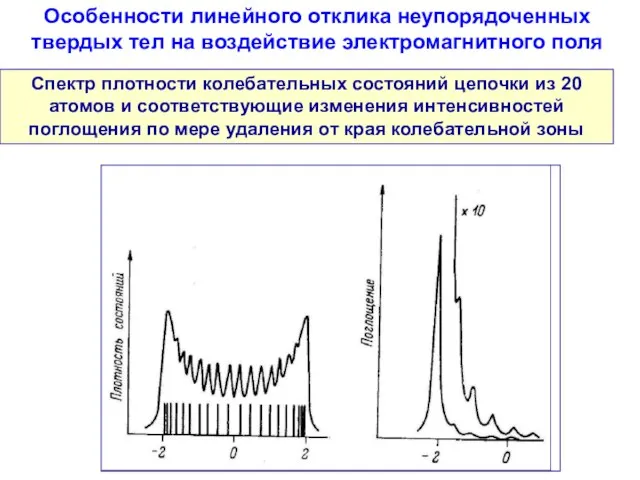
- 113. Спектр плотности колебательных состояний цепочки из 20 атомов и соответствующие изменения интенсивностей поглощения по мере удаления
- 114. V.2. Следствия неупорядоченности структуры для оптических свойств. V.2.2. Эмпирическое описание уширенных контуров полос поглощения. Простейший вариант:
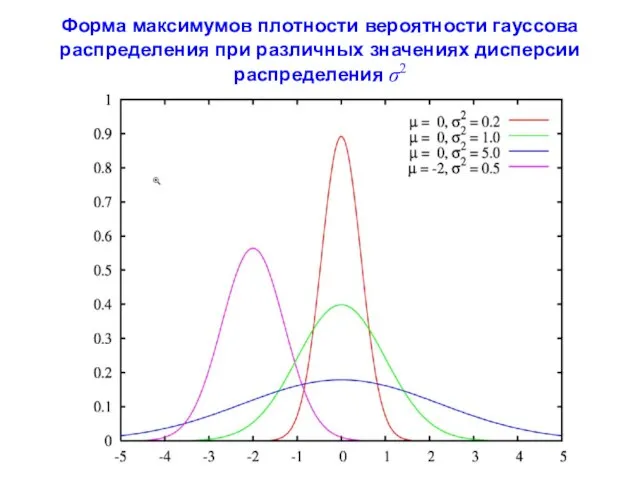
- 115. Форма максимумов плотности вероятности гауссова распределения при различных значениях дисперсии распределения σ2
- 116. V.2. Следствия неупорядоченности структуры для оптических свойств. V.2.2. Эмпирическое описание уширенных контуров полос поглощения (продолжение). Основываясь
- 117. V.3. Дисперсионное уравнение для комплексной диэ-лектрической проницаемости стекол (модель свертки). Для строгого учета влияния распределения осцилляторов
- 119. V.3. Дисперсионное уравнение для комплексной диэлектрической проницаемости стекол (аналитическая модель свертки - продолжение 1). В модели
- 120. V.3. Дисперсионное уравнение для комплексной диэлектрической проницаемости стекол (аналитическая модель свертки - продолжение 2). Действительная и
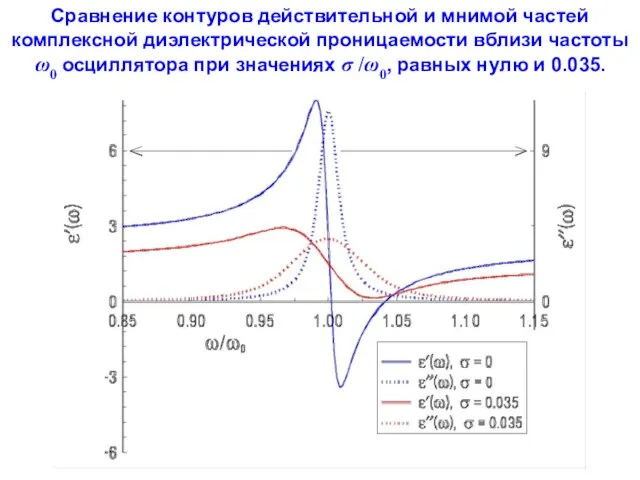
- 121. Сравнение контуров действительной и мнимой частей комплексной диэлектрической проницаемости вблизи частоты ω0 осциллятора при значениях σ
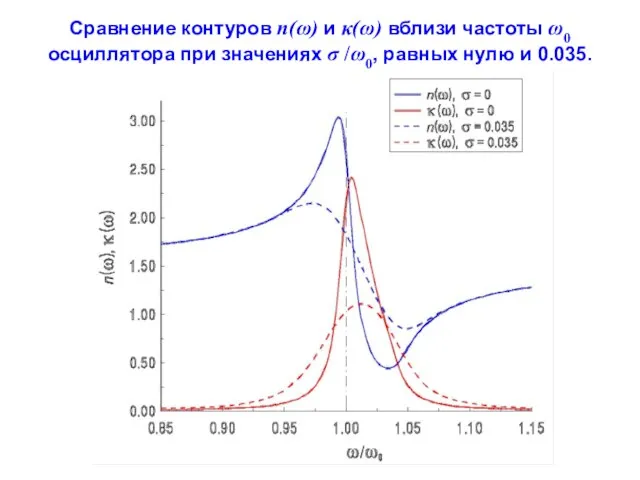
- 122. Сравнение контуров n(ω) и κ(ω) вблизи частоты ω0 осциллятора при значениях σ /ω0, равных нулю и
- 123. VI. Методы количественной обработки оптико-спектроскопических данных. При значениях показателя поглощения свыше 0.0001 прямое измерение значений показателя
- 124. VI.1. Методы двух углов и двух поляризаций. Для малых значений показателя поглощения существуют два метода прямого
- 125. VI.2. Метод Крамерса-Кронига. Метод Крамерса-Кронига базируется на использовании соотношения Крамерса-Кронига для фазового угла: Оно предусматривает интегрирование
- 126. VI.2. Метод Крамерса-Кронига (продолжение 1). В области энергий свыше 30 eV вид часто аппроксимируется степенной функцией
- 127. VI.2. Метод Крамерса-Кронига (продолжение 2). Значения фазового угла, полученные с помощью соотношения Крамерса-Кронига, используются вместе со
- 128. VI.3. Метод дисперсионного анализа. Метод дисперсионного анализа использует конкретную аналитическую модель дисперсии комплексной диэлектрической проницаемости, выбираемую
- 129. VI.3. Метод дисперсионного анализа (продолжение). Указанная функция невязки представляет собой среднеквадратичную ошибку, усредненную по всему спектру.
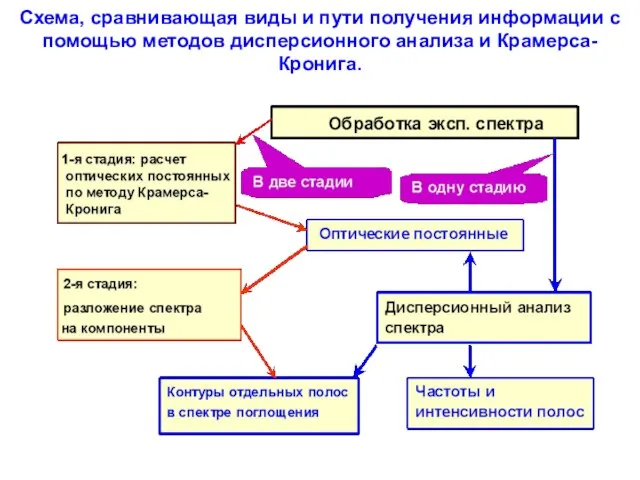
- 130. Схема, сравнивающая виды и пути получения информации с помощью методов дисперсионного анализа и Крамерса-Кронига.
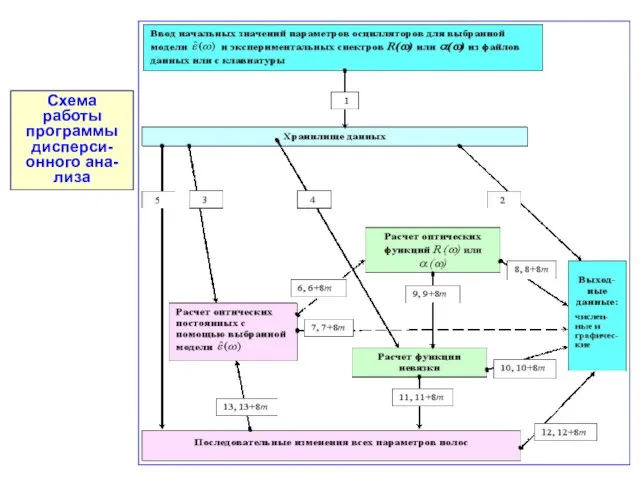
- 131. Схема работы программы дисперси-онного ана-лиза
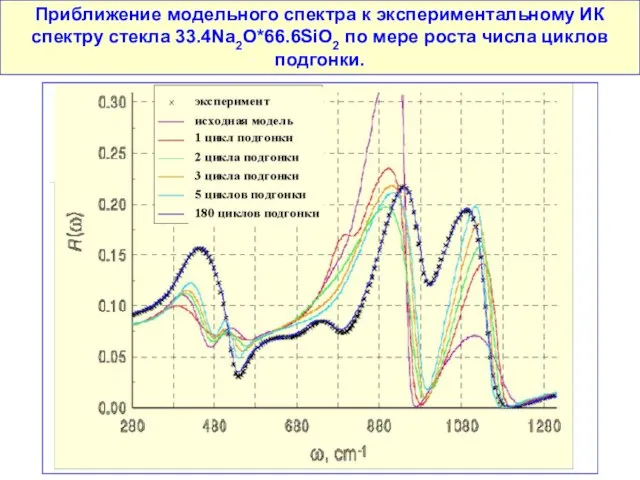
- 132. Приближение модельного спектра к экспериментальному ИК спектру стекла 33.4Na2O*66.6SiO2 по мере роста числа циклов подгонки.
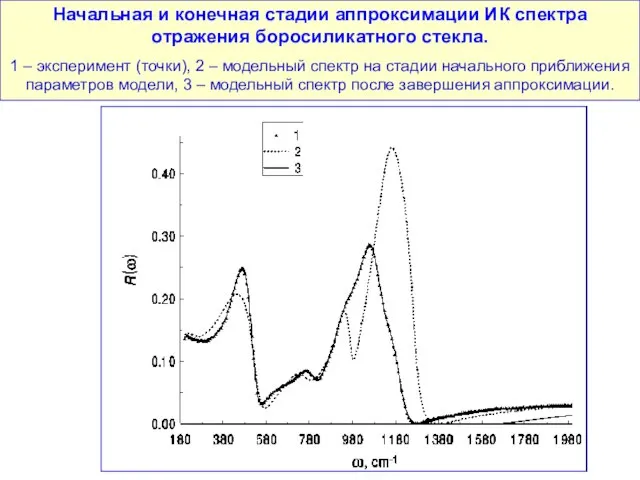
- 133. Начальная и конечная стадии аппроксимации ИК спектра отражения боросиликатного стекла. 1 – эксперимент (точки), 2 –
- 134. Разложение спектра примесного поглощения гидроксила и молекул воды в кварцевом стекле КУ1 на полосы поглощения.
- 135. Литература [1] Гарбуни М. Физика оптических явлений, М.: Машиностроение, 1967. – 517 с. [2] Борн М.,
- 137. Скачать презентацию




















































































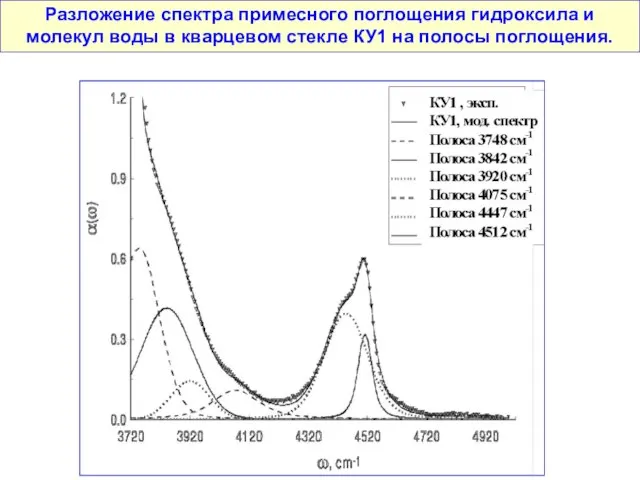
![Литература [1] Гарбуни М. Физика оптических явлений, М.: Машиностроение, 1967. – 517](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/382029/slide-134.jpg)
 Мировые океаны
Мировые океаны Силы природы
Силы природы Семейная викторина
Семейная викторина Вторая мировая война
Вторая мировая война Типичные ошибкипри проведении экспертизы
Типичные ошибкипри проведении экспертизы Фалсафа - 5
Фалсафа - 5 Москва
Москва Переломы пястных костей и фаланг пальцев
Переломы пястных костей и фаланг пальцев Персональный имидж учителя как средство формирования КОРПОРАТИВНОГО имиджа школы
Персональный имидж учителя как средство формирования КОРПОРАТИВНОГО имиджа школы Какая бывает промышленность?
Какая бывает промышленность? Функция
Функция Переосмысление образовательной среды. Реиновация интерьера холла колледжа
Переосмысление образовательной среды. Реиновация интерьера холла колледжа Клод Моне
Клод Моне Отряды млекопитающих
Отряды млекопитающих Что такое углеволокно (карбон) и как оно может спасти нас от нефтяного кризиса
Что такое углеволокно (карбон) и как оно может спасти нас от нефтяного кризиса Техника безопасности и форма одежды на уроках лыжной подготовки в школе
Техника безопасности и форма одежды на уроках лыжной подготовки в школе Рычаг и его удивительные свойства
Рычаг и его удивительные свойства Культура и искусство Китая
Культура и искусство Китая Виды дохода
Виды дохода 1. Икар хочет летать. 2. Поросёнок делает себе крылья. 3. Икар летит и падает. 4. Мама успокаивает поросёнка. 5. Волшебный источник хвали
1. Икар хочет летать. 2. Поросёнок делает себе крылья. 3. Икар летит и падает. 4. Мама успокаивает поросёнка. 5. Волшебный источник хвали Приемы мотивации. Диалоги на полях: чему нам имеет смысл учиться у тех, кого мы учим?
Приемы мотивации. Диалоги на полях: чему нам имеет смысл учиться у тех, кого мы учим? Аналитическая система мониторинга розничных продаж и управления клиентами
Аналитическая система мониторинга розничных продаж и управления клиентами Проблемное обучение
Проблемное обучение Применение производной в физике
Применение производной в физике Заповедники Архангельской области
Заповедники Архангельской области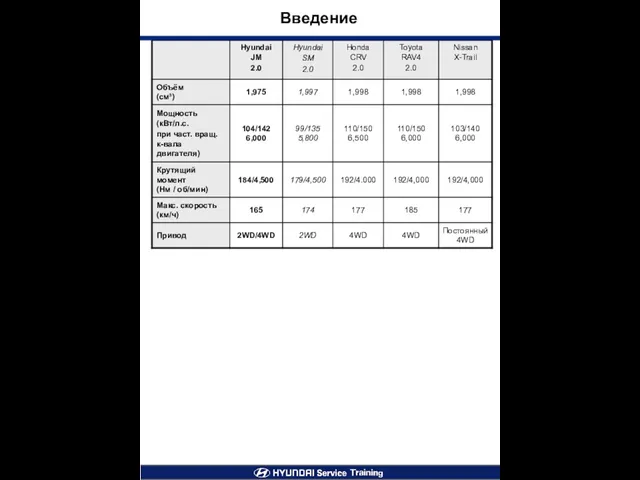 Введение
Введение Электронная коммерцияв розничных сетях VI конференция "Электроника: производство и торговля" 20 ноября 2009
Электронная коммерцияв розничных сетях VI конференция "Электроника: производство и торговля" 20 ноября 2009 Ломоносов и география
Ломоносов и география