Слайд 2Demand function
What shall we do with our selling Price, if:
P1 =

$1,000, then Q1 = 400 units, and R1 = $400,000
P2 = $1,750, then Q2 = 250 units, and R2 = $437,500
To do:
(a) increase the price, or
(b) decrease the price, or
(c) keep the price at $1,750?
SOLUTION: The price that MAX the revenue shall be: $2,250,
$2,000,
$1,750,
$1,500,
$1,250?
Слайд 3Demand function
Correct answer:
The “best” price to MAX the revenue would be:

$1,500
Popt = $1,500, then Qopt = 300 units, and RMAX = $450,000
To do:
(a) increase the price
(b) decrease the price
(c) keep the price at $1,750
This can be solved through (1) finding the demand function equation, and (2) solving a revenue maximization problem.
Слайд 4Demand function
Can be found using the approaches:
Sales tests:
P1, Q1
P2, Q2
NB: Demand

function is not always linear.
P(MAX) and Q(MAX) are indicative.
Sales test not always linear.
Need to offset the effect of seasonality.
Слайд 5Demand Function Equation
Y = a + b*X, basic linear equation
P = a

+ b*Q, demand function equation
where:
a = P(MAX in the market) = 3,000
b = slope of the demand function line
= delta Y/ delta X = -5
Q(MAX) = - a/b = 600 (units)
NB: Mind the negative value of the variable coefficient of the linear equation “b”.
Слайд 6Task: Revenue maximization
Q*(Revenue MAX) = - a/2b = 300 (u)
Substitute Q* into

the Demand function equation,
will find P* (= the price at Q* point)
P*= 3,000 +(-5)*300 = $1,500
R* = P* x Q* = 450,000
NB: R* is highest revenue possible at the current demand.
Слайд 7Profit maximization
Q** (Profit MAX) = - (a – VC(u)) / 2b
P** shall

correspond to the value of Q**
Data needed:
fixed and variable costs
FC = $100,000
VC(u) = $500
Q** = 250(u), then
P** = 1,750, then
R** = 437,500, and
Pr** = R** - FC – VC(u)Q** = $212,500
Pr** is highest operating profit possible at the current demand and total costs






 Композитинг. Что крайне рекомендуется учитывать для трекинга
Композитинг. Что крайне рекомендуется учитывать для трекинга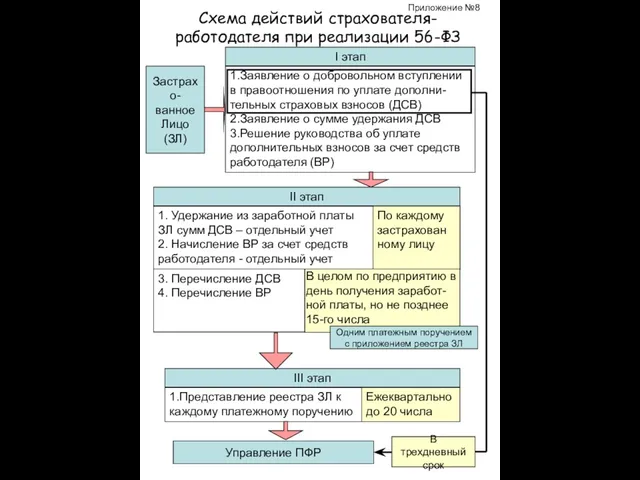 Схема действий страхователя-работодателя при реализации 56-ФЗ
Схема действий страхователя-работодателя при реализации 56-ФЗ Подготовка научных и научно-педагогических кадров Подготовили: Изотова Н. и Ахрюшина Ю.
Подготовка научных и научно-педагогических кадров Подготовили: Изотова Н. и Ахрюшина Ю. академик А.Л. Асеев председатель Сибирского отделения РАН
академик А.Л. Асеев председатель Сибирского отделения РАН Животные национальные символы стран мира
Животные национальные символы стран мира Единицы массы
Единицы массы Презентация на тему bmw
Презентация на тему bmw  Посуда
Посуда Кролики и зайцы
Кролики и зайцы Достижения Образцового коллектива-видеостудии СП МБОУДО ДДТ Синяя птица
Достижения Образцового коллектива-видеостудии СП МБОУДО ДДТ Синяя птица RAZREZY
RAZREZY Разработка дизайна образовательных пространств
Разработка дизайна образовательных пространств Возможности и перспективы сотрудничества ИПК МТУСИ с Ассоциацией ЭлектросвязьПроректор МТУСИ - директор ИПКВоскобович В.В.
Возможности и перспективы сотрудничества ИПК МТУСИ с Ассоциацией ЭлектросвязьПроректор МТУСИ - директор ИПКВоскобович В.В. Ценные бумаги
Ценные бумаги Бассейн Касатка. Платные образовательные услуги 2021-2022 учебный год
Бассейн Касатка. Платные образовательные услуги 2021-2022 учебный год Презентация на тему Классицизм в архитектуре Западной Европы
Презентация на тему Классицизм в архитектуре Западной Европы Портретный жанр. Станковая живопись
Портретный жанр. Станковая живопись Текстовый процессор Microsoft Word
Текстовый процессор Microsoft Word задачи
задачи Мужские часы
Мужские часы Структурные схемы устройств преобразования энергии первичных источников в электрическую. (Лекция 7)
Структурные схемы устройств преобразования энергии первичных источников в электрическую. (Лекция 7) Doubting Thomas
Doubting Thomas Наркотрафик
Наркотрафик Анализ деятельности МБОУ «Средняя общеобразовательная школа №40 им. Катасонова С.А.» за 1 полугодие 2011-2012 учебного года
Анализ деятельности МБОУ «Средняя общеобразовательная школа №40 им. Катасонова С.А.» за 1 полугодие 2011-2012 учебного года Мұнай өнер кәсібі. Мұнай өндеу және өнімдерін тұтыну. Халық саудасы
Мұнай өнер кәсібі. Мұнай өндеу және өнімдерін тұтыну. Халық саудасы Память и внимание
Память и внимание Зерновые корма Зерно злаковых содержит до 70% крахмала, 8–12% протеина, 2,2–10,3% клетчатки, 1,5–4% минеральных веществ и 2–8% жира. В нем со
Зерновые корма Зерно злаковых содержит до 70% крахмала, 8–12% протеина, 2,2–10,3% клетчатки, 1,5–4% минеральных веществ и 2–8% жира. В нем со Культурные особенности первых цивилизаций. Расцвет античной культуры. Лекция 2
Культурные особенности первых цивилизаций. Расцвет античной культуры. Лекция 2