Слайд 2Содержание
Введение
Оригами в геометрии
Аксиомы оригаметрии
Доказательство теорем с помощью оригами
Пример

решения задач
Заключение
Литература
Слайд 3Введение
Общее понятие об оригами.
Оригами -одно из традиционных японских искусств, а также

излюбленное развлечение японцев всех возрастов –малыши и пожилые люди с удовольствием складывают оригами в свободное время.
Целью данного проекта является доказательство того, что искусство оригами можно применять для доказательства теорем и для решения задач по геометрии.
Слайд 4Слово «оригами» переводится как «сложенная бумага» (ори-ками). А «ками» по-японски это и

«бумага», и «Бог». Поэтому японцы с особым почтением относится к искусству складывания. В древней Японии бумажные фигурки участвовали в религиозных обрядах, а позднее очень полюбились при императорском дворе. Умение складывать было признаком хорошего образования и тонкого изысканного вкуса.
Слайд 8Оригами в геометрии
Оригами используется в геометрии -для доказательства теорем и решения задач.

Решение задач с помощью оригаметрии –способ необычный и интересный, так как многие понятия школьного курса геометрии просто и наглядно объясняются демонстрацией оригами.
Слайд 9Оригаметрия –область очень молодая, и пока не существует ни соответствующих программ, ни

учебников, которые давали бы подобный материал систематически. Вместе с тем многие понятия курса геометрии в школе гораздо проще и нагляднее объясняются с помощью оригаметрии.
Слайд 11Аксиомы оригаметрии.
Для построения теории используется система аксиом. Действительно, аксиомы оригаметрии существуют! Их

предложил живущий в Италии японский математик Хумиани Хузита.
Слайд 12Таких аксиом, с его точки зрения, всего шесть.
Аксиома 1. Существует единственный сгиб,
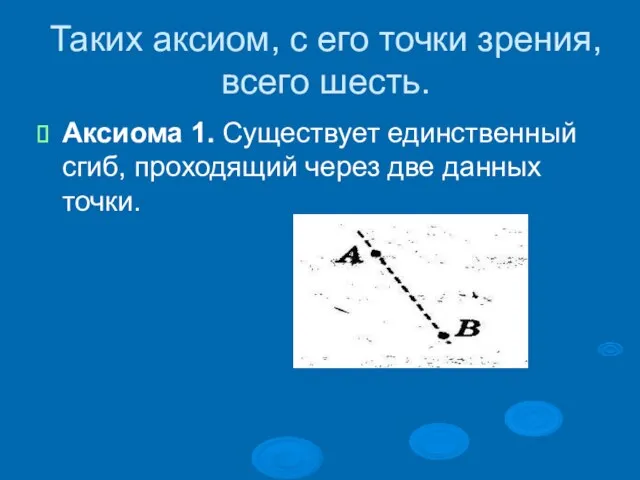
проходящий через две данных точки.
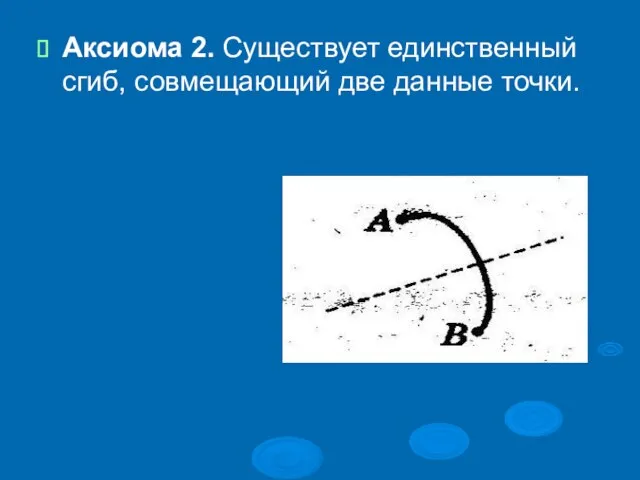
Слайд 13Аксиома 2. Существует единственный сгиб, совмещающий две данные точки.
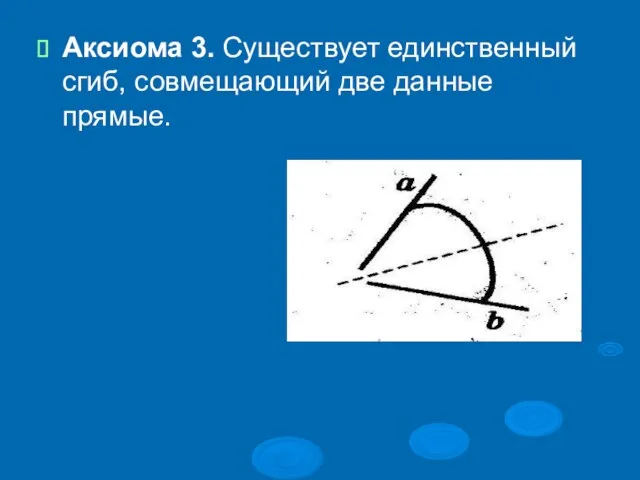
Слайд 14Аксиома 3. Существует единственный сгиб, совмещающий две данные прямые.
Слайд 15Аксиома 4. Существует единственный сгиб, проходящий через данную точку и перпендикулярный данной
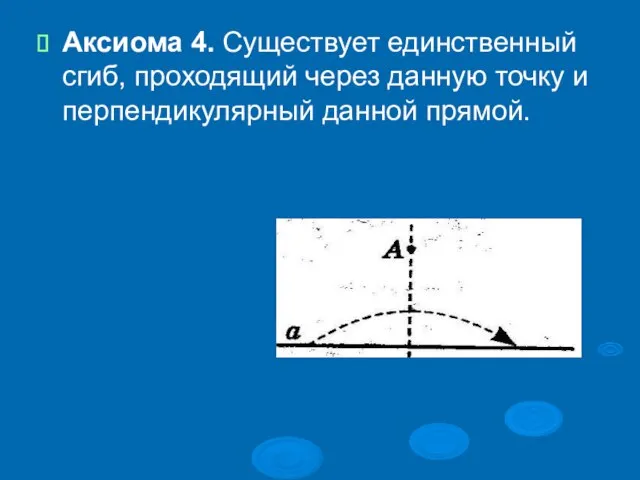
прямой.
Слайд 16Аксиома 5. Существует единственный сгиб, проходящий через данную точку и помещающий другую
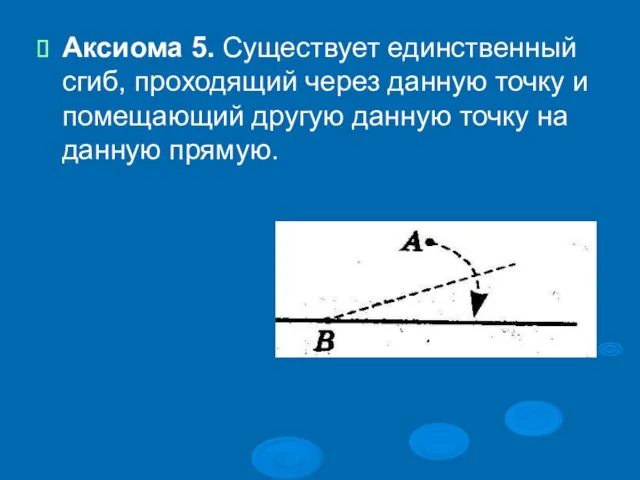
данную точку на данную прямую.
Слайд 17Аксиома 6. Существует единственный сгиб, помещающий каждую из двух данных точек на

одну из двух данных пересекающихся прямых.
Слайд 18В 2002 году японский оригамист Коширо Хатори обнаружил сгиб, который не описан

в аксиомах Х. Хузита.
Аксиома 7. Для двух данных прямых и точки существует линия сгиба. Перпендикулярная первой прямой и помещающая данную точку на вторую прямую.
Слайд 19Доказательство теорем с помощью оригами.
Теорема 1.Суммауглов треугольника равна 180 градусов.
Доказательство. Возьмем лист

бумаги, имеющий форму произвольного треугольника.
Слайд 201) Проведем сгиб через одну из вершин треугольника, перпендикулярно противоположной стороне (высоту
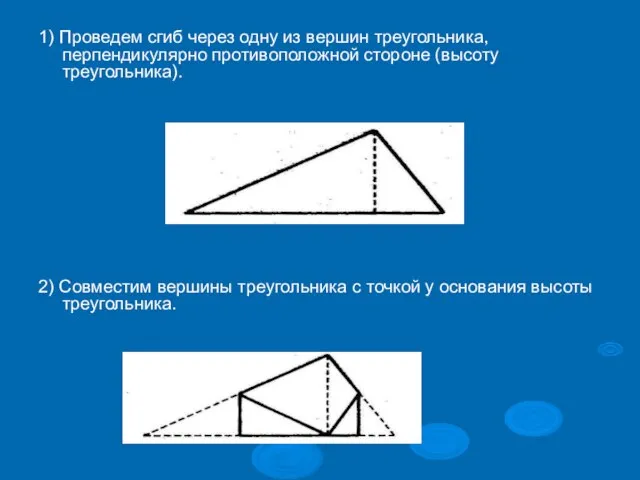
треугольника).
2) Совместим вершины треугольника с точкой у основания высоты треугольника.
22
Слайд 213)Получаем, что углы 1, 2 и 3 треугольника совпали при наложении с

развернутым углом, следовательно, сумма углов равна 180 градусов.
Слайд 22Теорема 2. Накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей,

равны.
1) Доказательство. Возьмем лист бумаги с двумя параллельными сторонами и секущей АВ. Сравним накрест лежащие углы- углы 1 и 2.
24
Слайд 232) Совместим вершины накрест лежащих углов- точки А и В.
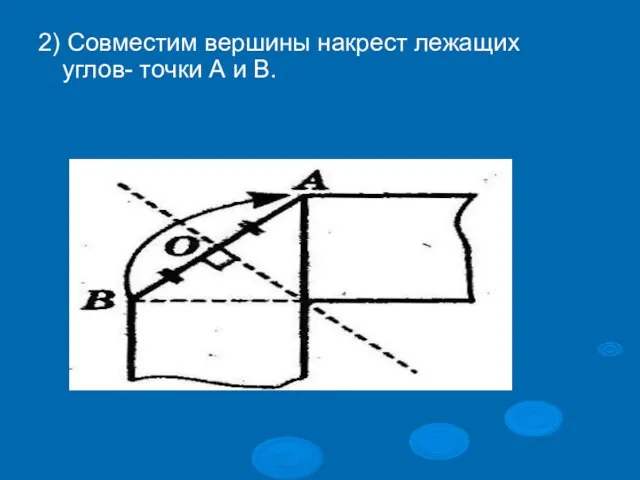
Слайд 24
3)Углы 1 и 2 совпали при наложении, следовательно, угол 1 равен углу
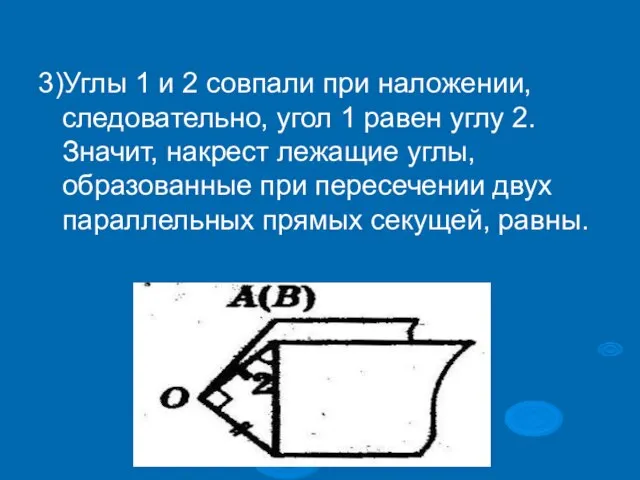
2. Значит, накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей, равны.
Слайд 25Пример решения задач.
Задача
Прямая, проходящая через середину биссектрисы AD треугольника АВС и перпендикулярная

AD, пересекает сторону АС в точке М.
Доказать, что MD //AB.
Слайд 26Решение
Возьмем лист бумаги, имеющий форму производного треугольника. Проведем биссектрису AD, согнув лист

так, чтобы сторона АС совместилась со стороной АВ. Наметим середину АD, совместив точки А и D. Проведем ОМ, перпендикулярную AD. Согнем лист по линии MD.
Слайд 27Для доказательства параллельности MD и АВ сравним углы 1 и 3, для
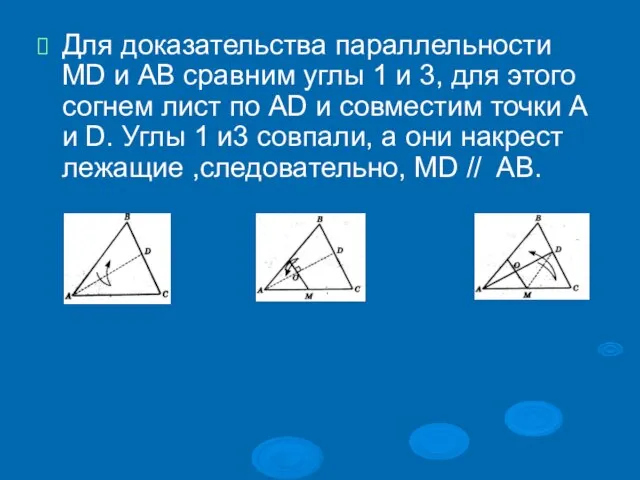
этого согнем лист по AD и совместим точки А и D. Углы 1 и3 совпали, а они накрест лежащие ,следовательно, MD // AB.
Слайд 28Заключение
Таким образом, мы смогли доказать, что решать геометрические задачи с помощью оригами

достаточно просто и интересно, так как многие понятия школьного курса геометрии наглядно объясняются демонстрацией оригами.
Слайд 29Литература
Афонькин С.Ю. Уроки оригами в школе и дома.- М.: Аким, 1996.
http://sch139.5ballov.ru/doom/-дистанционная обучающая

олимпиада по математике.




























 Химия в жизни общества
Химия в жизни общества Тема презентации. Шаблон
Тема презентации. Шаблон Как рисовать деревья
Как рисовать деревья ФОРМАЛИЗАЦИЯ МОДЕЛЕЙ ОБРАБОТКИ ДАННЫХ
ФОРМАЛИЗАЦИЯ МОДЕЛЕЙ ОБРАБОТКИ ДАННЫХ Что такое самопрезентация?
Что такое самопрезентация? Ассоциация «Белорусская федерация футбола»
Ассоциация «Белорусская федерация футбола» КАТЕГОРИЯ ЭЛЕКТРИКА
КАТЕГОРИЯ ЭЛЕКТРИКА  Некоммерческое партнерство «Межрегиональный институт сертифицированных бухгалтеров и финансовых менеджеров» (НП МИСБФМ)
Некоммерческое партнерство «Межрегиональный институт сертифицированных бухгалтеров и финансовых менеджеров» (НП МИСБФМ) Презентация на тему История развития зоологии. Современная зоология
Презентация на тему История развития зоологии. Современная зоология Приветствуем Вас на неделе естественнонаучного цикла
Приветствуем Вас на неделе естественнонаучного цикла Каким я хочу видеть свой город в будущем.
Каким я хочу видеть свой город в будущем. Этапы выполнения исследовательской работы. Оформление НИР
Этапы выполнения исследовательской работы. Оформление НИР Схемы диапазонных РПУ
Схемы диапазонных РПУ ПРАВИЛА ПРИЕМА В ИНСТИТУТ
ПРАВИЛА ПРИЕМА В ИНСТИТУТ Дар предвосхищения
Дар предвосхищения Презентация на тему Искусство скифов
Презентация на тему Искусство скифов  Теория гимнастики и акробатики
Теория гимнастики и акробатики Взаимодействие заряженных тел
Взаимодействие заряженных тел Третьи региональные соревнования профессионального мастерства WSR по Московской области по компетенции Машинист локомотива
Третьи региональные соревнования профессионального мастерства WSR по Московской области по компетенции Машинист локомотива Философия древней греции
Философия древней греции Акции к юбилею Арт Лайф
Акции к юбилею Арт Лайф Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint GERSOG. Ваш индивидуальный фотограф
GERSOG. Ваш индивидуальный фотограф Внешняя политика России
Внешняя политика России Категория состояния
Категория состояния тема проекта:
тема проекта: Долговая политика и источники финансирования муниципальных программ - инструменты экономического роста
Долговая политика и источники финансирования муниципальных программ - инструменты экономического роста Насилие среди сверстников
Насилие среди сверстников