Содержание
- 2. Содержание Симметрия Осевая симметрия Задачи Симметрия в геометрии, природе, архитектуре, поэзии Заключение
- 3. Определение Симметрия (от греч. Symmetria – соразмерность), в широком смысле – неизменность структуры материального объекта относительно
- 4. Осевая симметрия Две точки, лежащие на одном перпендикуляре к данной прямой по разные стороны и на
- 5. Фигура называется симметричной относительно прямой a, если для каждой точки фигуры симметричная ей точка относительно прямой
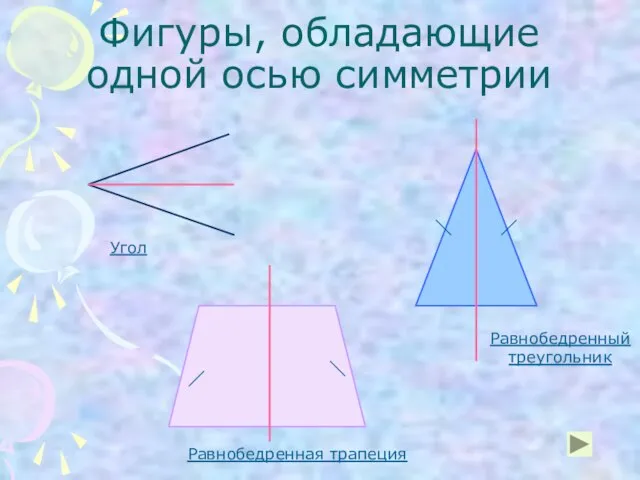
- 6. Фигуры, обладающие одной осью симметрии Угол Равнобедренный треугольник Равнобедренная трапеция
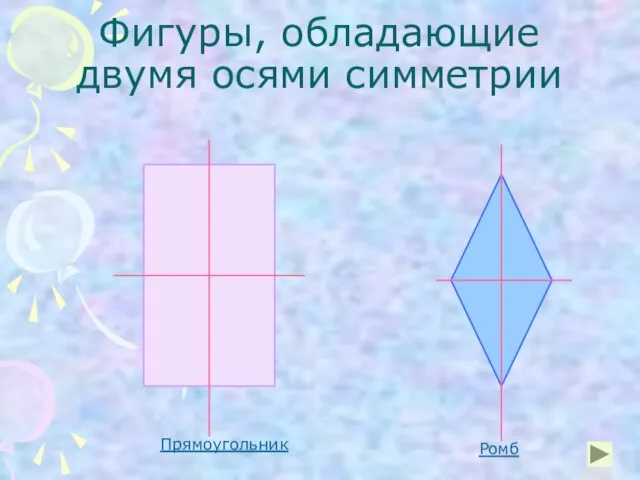
- 7. Фигуры, обладающие двумя осями симметрии Прямоугольник Ромб
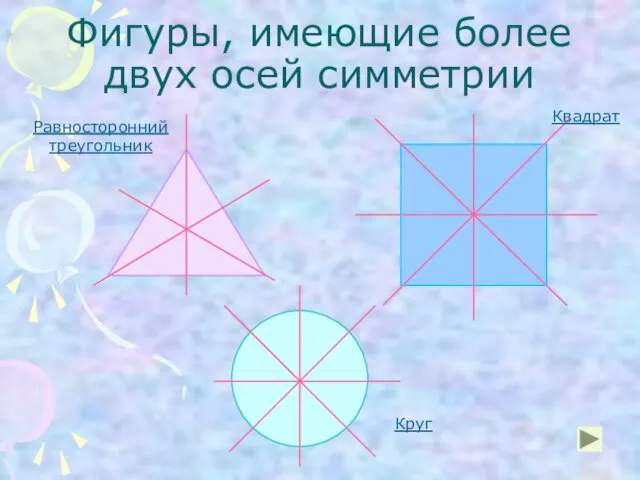
- 8. Фигуры, имеющие более двух осей симметрии Равносторонний треугольник Квадрат Круг
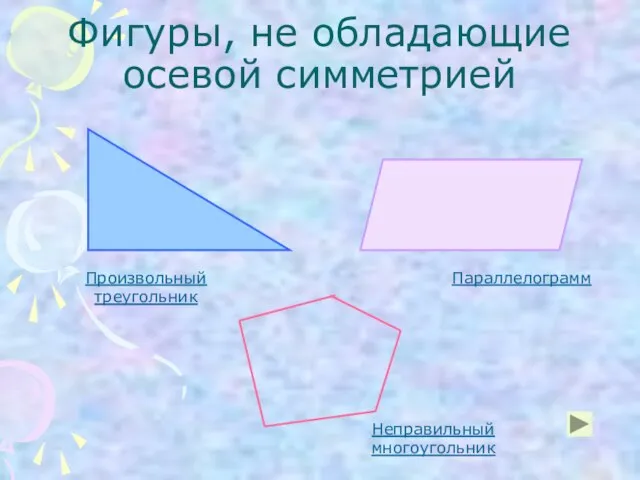
- 9. Фигуры, не обладающие осевой симметрией Произвольный треугольник Параллелограмм Неправильный многоугольник
- 10. Построение точки, симметричной данной отрезка, симметричного данному треугольника, симметричного данному
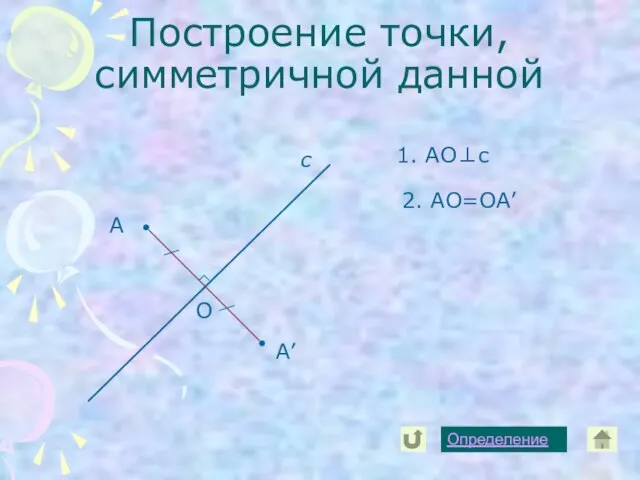
- 11. Построение точки, симметричной данной А с А’ Определение 1. АО⊥с О 2. АО=ОА’
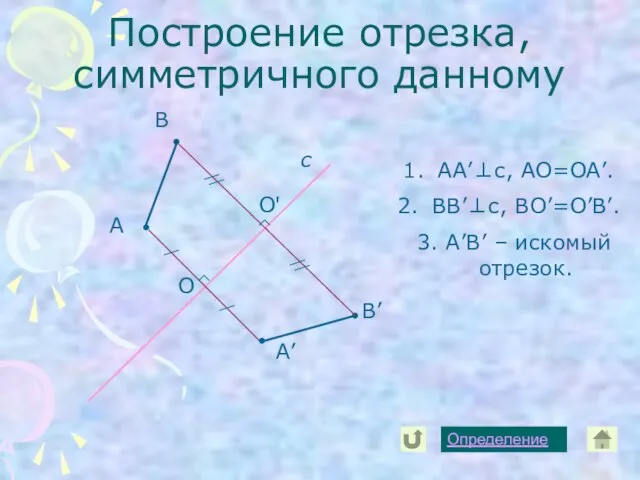
- 12. Построение отрезка, симметричного данному А с А’ В В’ Определение O O' АА’⊥с, АО=ОА’. ВВ’⊥с, ВО’=О’В’.
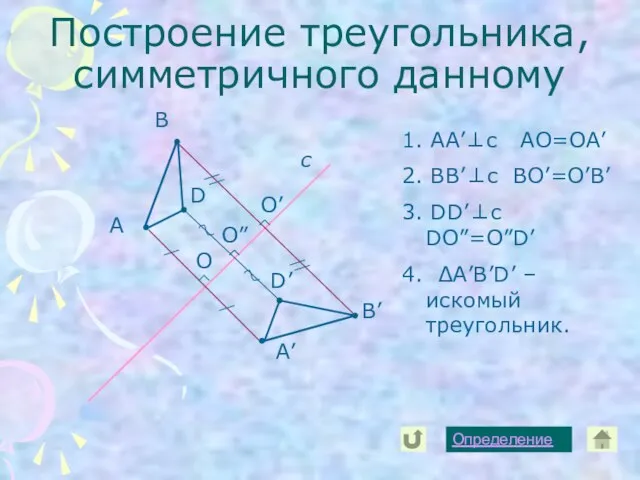
- 13. Построение треугольника, симметричного данному А с А’ В В’ D D’ Определение 1. AA’⊥c AO=OA’ 2.
- 14. Задачи 1. Отрезок АВ, перпендикулярный прямой с, пересекает ее в точке О так, что АО≠ОВ. Симметричны
- 15. Задачи 1. Отрезок АВ, перпендикулярный прямой с, пересекает ее в точке О так, что АО≠ОВ. Симметричны
- 16. 4. Изобразите точку А, лежащую в I четверти координатной плоскости. Точка В симметрична точке А относительно
- 17. Ответ: Точки A и D симметричны относительно оси х. ABCD – прямоугольник Если расстояния от точки
- 18. 5. Относительно какой из координатных осей симметричны точки М(7;2) и К(-7;2)? 6. Точки А(5;…) и В(…;2)
- 19. Проверь себя 5. Ответ: Оу. 6. Ответ: А(5;-2) и В(5;2). 7. Ответ: С(2;-3). 8. Ответ: В(1;3)
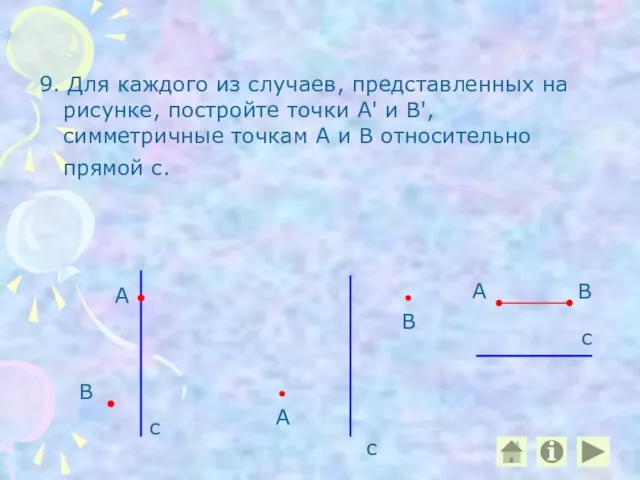
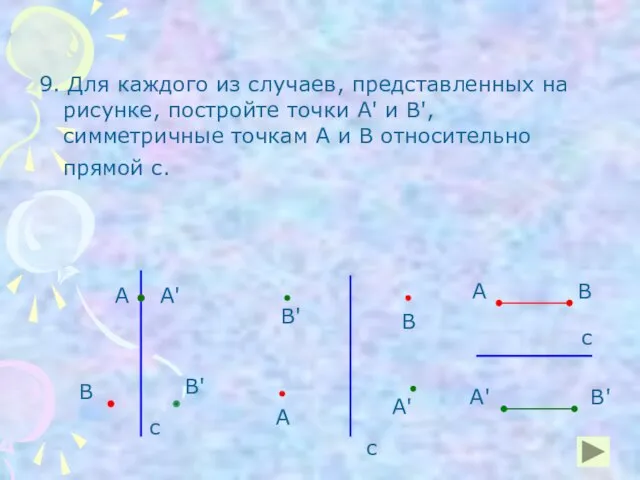
- 20. 9. Для каждого из случаев, представленных на рисунке, постройте точки А' и В', симметричные точкам А
- 21. 9. Для каждого из случаев, представленных на рисунке, постройте точки А' и В', симметричные точкам А
- 22. 10. Постройте треугольники, симметричные данным, относительно прямой с. с с
- 23. 10. Постройте треугольники, симметричные данным, относительно прямой с. с с
- 24. 11. Начертите две прямые а и b и отметьте две точки А и В так, чтобы
- 25. Подсказка Для решения задачи рекомендуется сначала отметить точку С, а лишь потом отмечать точки А и
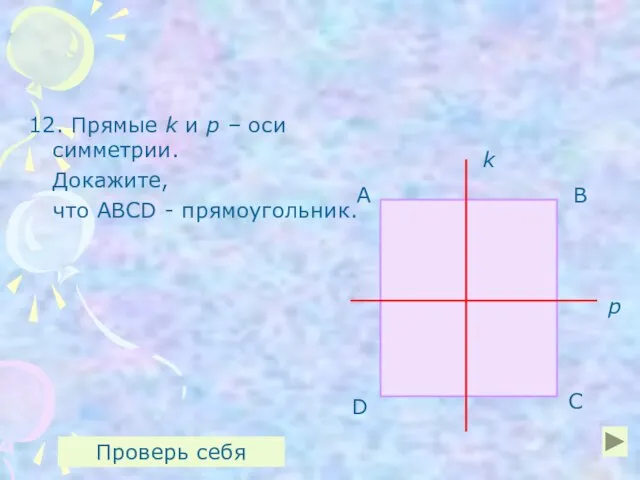
- 26. 12. Прямые k и р – оси симметрии. Докажите, что ABCD - прямоугольник. k р А
- 27. Доказательство: Так как k – ось симметрии, то ∠А=∠D, ∠В=∠С. Так как р – ось симметрии,
- 28. Симметрия в природе
- 29. В архитектуре
- 30. Пушкин А.С. «Медный всадник» …В гранит оделася Нева; Мосты повисли над водами; Темнозелеными садами Ее покрылись
- 32. Скачать презентацию



















 Влияние компьютерной системы с использованием sms-сообщений на контроль АД у больных артериальной гипертонией
Влияние компьютерной системы с использованием sms-сообщений на контроль АД у больных артериальной гипертонией CAREER OR FAMILY
CAREER OR FAMILY  Ремёсла восточных славян
Ремёсла восточных славян Немецкий шоколад торговой марки Lubeca (Германия)
Немецкий шоколад торговой марки Lubeca (Германия) Презентация на тему Технология моделирования в начальной школе
Презентация на тему Технология моделирования в начальной школе Светлое воскресение христово
Светлое воскресение христово М.В. Ломоносов как экономист и статистик
М.В. Ломоносов как экономист и статистик Describing people
Describing people  Дети капитана Гранта
Дети капитана Гранта Багълайыджылар
Багълайыджылар Дидактическое сопровождение и структура занятий с детьми дошкольного возраста.
Дидактическое сопровождение и структура занятий с детьми дошкольного возраста. Презентация на тему Творчество В. П. Крапивина в моем понимании «Какая–то тихая популярность!»
Презентация на тему Творчество В. П. Крапивина в моем понимании «Какая–то тихая популярность!»  Презентация на тему Образ Снегурочки в русском искусстве и литературе
Презентация на тему Образ Снегурочки в русском искусстве и литературе 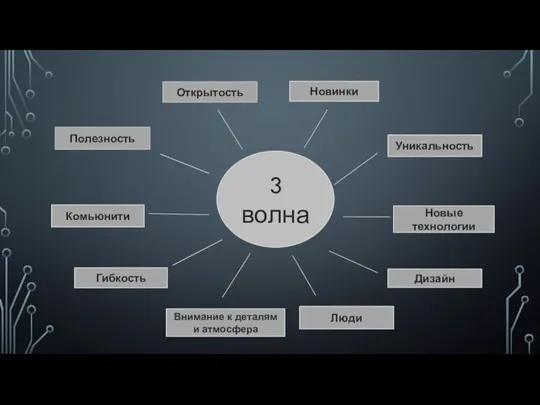 Необходимые навыки для создания компании 3 волны
Необходимые навыки для создания компании 3 волны Презентация на тему Жизнь вельможи
Презентация на тему Жизнь вельможи Презентация на тему Основы безопасности жизнедеятельности 11 класс
Презентация на тему Основы безопасности жизнедеятельности 11 класс  Нормативно-правовые акты, гарантирующие право получения детям с ограниченными возможностями здоровья адекватного их возможностя
Нормативно-правовые акты, гарантирующие право получения детям с ограниченными возможностями здоровья адекватного их возможностя Фундаментальный курс по стрижкам
Фундаментальный курс по стрижкам О путях развития информационно- вычислительных систем в области внегалактических исследований
О путях развития информационно- вычислительных систем в области внегалактических исследований Леса России
Леса России МОУ Андрейковская средняя школаВяземского района Смоленской области«Внедрение инновационных образовательных проектов в практ
МОУ Андрейковская средняя школаВяземского района Смоленской области«Внедрение инновационных образовательных проектов в практ ПСИХОЛОГО-ПЕДАГОГИЧЕСКОЕ СОПРОВОЖДЕНИЕ ВВЕДЕНИЯФГОС НОО
ПСИХОЛОГО-ПЕДАГОГИЧЕСКОЕ СОПРОВОЖДЕНИЕ ВВЕДЕНИЯФГОС НОО Қазіргі замандағы әлемдік діндер
Қазіргі замандағы әлемдік діндер Презентация на тему Ледники
Презентация на тему Ледники  Семинар
Семинар Основы радиосвязи
Основы радиосвязи Exploring space
Exploring space ТЗ на подготовку лендинга для круизов
ТЗ на подготовку лендинга для круизов