Основные элементы однофазных цепей переменного тока

Элементы электрической цепи синусоидального тока
Основные свойства простейших цепей переменного тока
Простейшие цепи – цепи, содержащие один элемент.

Участок цепи, содержащий идеальную индуктивность
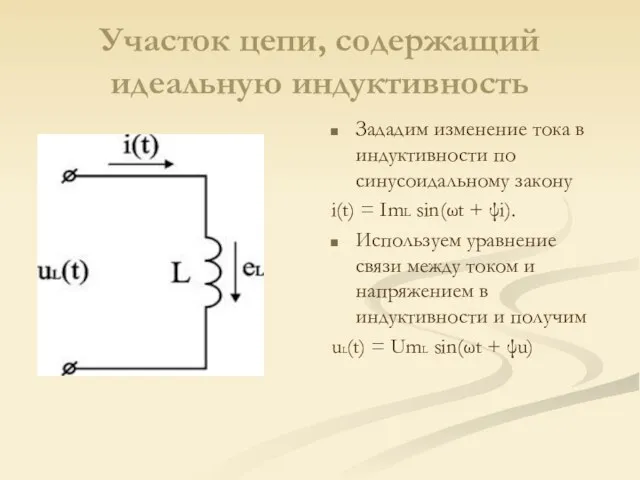
Зададим изменение тока в индуктивности по синусоидальному закону
i(t) = ImL sin(ωt + ψi).
Используем уравнение связи между током и напряжением в индуктивности и получим
uL(t) = UmL sin(ωt + ψu)

Участок цепи, содержащий идеальную индуктивность
Соотношения будут равны если выполняется условие равенства амплитуд и фаз
UmL = ωL · ImL
ψu = ψi + 90°
Уравнение можно переписать для действующих значений
UL = ωL · IL
Уравнение показывает, что фаза тока в индуктивности отстает от фазы напряжения на 90°
Величину XL = ωL в уравнении называют индуктивным сопротивлением. Единицей его измерения является Ом.

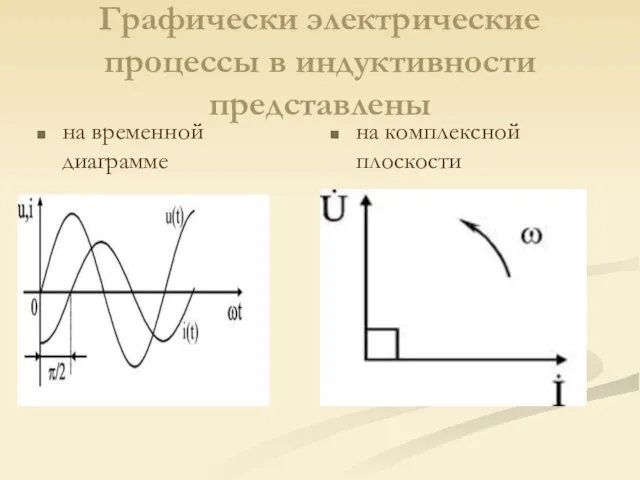
Графически электрические процессы в индуктивности представлены
на временной диаграмме
на комплексной плоскости

Сопротивления в цепи переменного тока
Реактивное.
В разделе реактивные выделяют три вида сопротивлений:
индуктивное xL
емкостное хс
собственно реактивное.
Для индуктивного сопротивления выше была получена формула XL = ωL
Единицей измерения индуктивного сопротивления также является Ом.
Величина xL линейно зависит от частоты.

Элемент L (индуктивность)
Известно, что в индуктивности соотношение фаз ψu = ψi + 90°.
Для мгновенной мощности имеет
Для количественной оценки мощности в индуктивности используют величину QL равную максимальному значению рL
QL = (Um Im) / 2 и называют ее реактивной (индуктивной) мощностью.
Единицей ее измерения выбрали ВАр
(вольт-ампер реактивный).