Основные определения в моделировании

Вопрос № 2
Общие понятия моделирования
Модель - объект или описание объекта, системы для замещения (при определенных условиях предложениях, гипотезах) одной системы (т.е. оригинала) другой системы для изучения оригинала или воспроизведения его каких - либо свойств. Модель - результат отображения одной структуры на другую. Отображая физическую систему (объект) на математическую систему (например, математический аппарат уравнений) получим физико - математическую модель системы или математическую модель физической системы. В частности, физиологическая система - система кровообращения человека, подчиняется некоторым законам термодинамики и описав эту систему на физическом (термодинамическом) языке получим физическую, термодинамическую модель физиологической системы. Если записать эти законы на математическом языке, например, выписать соответствующие термодинамические уравнения, то получим математическую модель системы кровообращения.

Вопрос № 3
Общие типы моделей
Модели, если отвлечься от областей, сфер их применения, бывают трех типов: познавательные, прагматические и инструментальные.
Познавательная модель - форма организации и представления знаний, средство соединение новых и старых знаний. Познавательная модель, как правило, подгоняется под реальность и является теоретической моделью.
Прагматическая модель - средство организации практических действий, рабочего представления целей системы для ее управления. Реальность в них подгоняется под некоторую прагматическую модель. Это, как правило, прикладные модели.
Инструментальная модель - является средством построения, исследования и/или использования прагматических и/или познавательных моделей.
Познавательные отражают существующие, а прагматические - хоть и не существующие, но желаемые и, возможно, исполнимые отношения и связи.

Вопрос 4. Классификация моделей
Модель называется статической если входные и выходные воздействия постоянны во времени. Статическая модель описывает установившийся режим.
Модель - динамическая, если входные и выходные переменные изменяются во времени. Динамическая модель описывает неустановившийся режим работы изучаемого объекта.
Модель - дискретная, если она описывает поведение системы только в дискретные моменты времени.
Модель - непрерывная, если она описывает поведение системы для всех моментов времени из некоторого промежутка времени.
Модель - имитационная, если она предназначена для испытания или изучения, проигрывания возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели.
Модель - детерминированная, если каждому входному набору параметров соответствует вполне определенный и однозначно определяемый набор выходных параметров; в противном случае - модель недетерминированная, стохастическая (вероятностная).

Вопрос 5. Свойства модели
Свойства любой модели таковы:
• конечность: модель отображает оригинал лишь в конечном числе его отношений и, кроме того, ресурсы моделирования конечны;
• упрощенность: модель отображает только существенные стороны объекта;
• приблизительность: действительность отображается моделью грубо или приблизительно;
• адекватность: модель успешно описывает моделируемую систему;
• информативность: модель должна содержать достаточную информацию о системе - в рамках гипотез, принятых при построении модели.
В основе моделирования лежит теория подобия (замена одного объекта точно таким же другим).
Подобия подразделяются:
1. Полное (идеальное) которое в практике моделирования достичь очень трудно;
2. Неполное;
3. Приближенное.

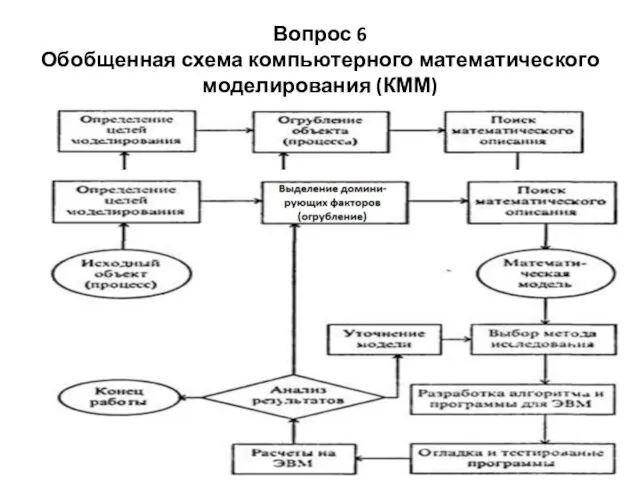
Вопрос 6
Обобщенная схема компьютерного математического моделирования (КММ)

Вопрос 7
Содержание основных этапов КММ
Определение целей моделирования:
1) модель нужна для того, чтобы понять как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром (понимание);
2) модель нужна для того, чтобы научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях (управление);
3) модель нужна для того, чтобы прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект (прогнозирование).

Важнейшим этапом моделирования является разделение входных параметров по степени важности влияния их изменений на выходные. Такой процесс называется ранжированием (разделением по рангам). Чаще всего невозможно (да и не нужно) учитывать все факторы, которые могут повлиять на значения интересующих величин. От того, насколько умело выделены важнейшие факторы, зависит успех моделирования, быстрота и эффективное для достижения цели. Выделить более важные (значимые) факторы и отсеять менее важные может лишь специалист в той предметной области, к которой относится модель.

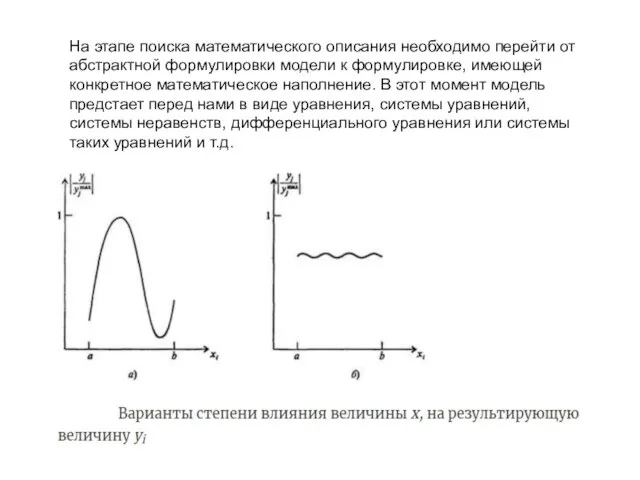
На этапе поиска математического описания необходимо перейти от абстрактной формулировки модели к формулировке, имеющей конкретное математическое наполнение. В этот момент модель предстает перед нами в виде уравнения, системы уравнений, системы неравенств, дифференциального уравнения или системы таких уравнений и т.д.

Когда математическая модель сформулирована, выбираем метод ее исследования. Как правило, для решения одной и той же задачи есть несколько конкретных методов, различающихся эффективностью, устойчивостью и т.д. От верного выбора метода часто зависит успех всего процесса.
После составления программы решаем с ее помощью простейшую тестовую задачу (желательно, с заранее известным ответом) с целью устранения грубых ошибок. Это -лишь начало процедуры тестирования, которую трудно описать формально исчерпывающим образом. По существу, тестирование может продолжаться долго и закончиться тогда, когда пользователь по своим профессиональным признакам сочтет программу верной.
Затем следует собственно численный эксперимент, и выясняется, соответствует ли модель реальному объекту (процессу). Модель адекватна реальному процессу, если некоторые характеристики процесса, полученные на ЭВМ, совпадают с экспериментальными с заданной степенью точности. В случае несоответствия модели реальному процессу возвращаемся к одному из предыдущих этапов.

Вопрос 8. Жизненный цикл моделируемой системы
1. Сбор информации об объекте, выдвижение гипотез, предмодельный анализ;
2. Проектирование структуры и состава моделей (подмоделей);
3. Построение спецификаций модели, разработка и отладка отдельных подмоделей, сборка модели в целом, идентификация (если это нужно) параметров моделей;
4. Исследование модели - выбор метода исследования и разработка алгоритма (программы) моделирования;
5. Исследование адекватности, устойчивости, чувствительности модели;
6. Оценка средств моделирования (затраченных ресурсов);
7. Интерпретация, анализ результатов моделирования и установление некоторых причинно - следственных связей в исследуемой системе;
8. Генерация отчетов и проектных (народно - хозяйственных) решений;
9. Уточнение, модификация модели, если это необходимо, и возврат к исследуемой системе с новыми знаниями, полученными с помощью моделирования.

Вопрос 9. Численные операции над моделями
1. Линеаризация. Пусть М=М(X,Y,A), где X - множество входов, Y - выходов, А - состояний системы. Схематически можно это изобразить:
X -> A -> Y
Если X, Y, A - линейные пространства (множества), а - линейные операторы, то система (модель) называется линейной. Другие системы (модели) - нелинейные. Нелинейные системы трудно поддаются исследованию, поэтому их часто линеаризуют - сводят к линейным каким-то образом.
2. Идентификация. Пусть М=М(X,Y,A), A={ai }, ai=(ai1,ai2,...,aik) - вектор состояния объекта (системы). Если вектор ai зависит от некоторых неизвестных параметров, то задача идентификации (модели, параметров модели) состоит в определении по некоторым дополнительным условиям, например, экспериментальным данным, характеризующим состояние системы в некоторых случаях. Идентификация - решение задачи построения по результатам наблюдений математических моделей, описывающих адекватно поведение реальной системы.
3. Агрегирование. Операция состоит в преобразовании (сведении) модели к модели (моделям) меньшей размерности (X, Y, A).

4. Декомпозиция. Операция состоит в разделении системы (модели) на подсистемы (подмодели) с сохранением структур и принадлежности одних элементов и подсистем другим.
5. Сборка. Операция состоит в преобразовании системы, модели, реализующей поставленную цель из заданных или определяемых подмоделей (структурно связанных и устойчивых).
6. Макетирование. Эта операция состоит в апробации, исследовании структурной связности, сложности, устойчивости с помощью макетов или подмоделей упрощенного вида, у которых функциональная часть упрощена (хотя вход и выход подмоделей сохранены).
7. Экспертиза, экспертное оценивание. Операция или процедура использования опыта, знаний, интуиции, интеллекта экспертов для исследования или моделирования плохо структурируемых, плохо формализуемых подсистем исследуемой системы.
8. Вычислительный эксперимент. Это эксперимент, осуществляе-мый с помощью модели на ЭВМ с целью распределения, прогноза тех или иных состояний системы, реакции на те или иные входные сигналы. Прибором эксперимента здесь является компьютер.

Вопрос 10. Области использования моделей
Модели и моделирование применяются по следующим основным и важным направлениям.
1.Обучение (как моделям, моделированию, так и самих моделей).
2.Познание и разработка теории исследуемых систем - с помощью каких - то моделей, моделирования, результатов моделирования.
3.Прогнозирование (выходных данных, ситуаций, состояний системы).
4.Управление (системой в целом, отдельными подсиситемами системы, выработка управленческих решений и стратегий).
5.Автоматизация (системы или отдельных подсистем системы).
В базовой четверке информатики: "модель - алгоритм - компьютер - технология" при компьютерном моделировании главную роль играют уже алгоритм (программа), компьютер и технология (точнее, инструментальные системы для компьютера, компьютерные технологии).
Например, при имитационном моделировании (при отсутствии строгого и формально записанного алгоритма) главную роль играют технология и средства моделирования.

Вопрос 11. Макетирование (физическое моделирование)
Макетирование осуществляется путем воспроизведения исследуемого процесса на физической модели, имеющей в общем случае отличную от оригинала природу, но одинаковое математическое описание процесса функционирования. Это метод экспериментального изучения различных физических явлений, основанный на их физическом подобии. Применяется при условии отсутствия точного математического описания процесса, или описание слишком громоздко и требует для расчётов большого объёма исходных данных, получение которых затруднительно.
Воспроизведение исследуемого физического явления в целях эксперимента в реальном масштабе времени слишком дорогостояще. Обычно осуществляется создание лабораторной физической модели в уменьшенных масштабах, и проведении на ней экспериментов.
Выводы и данные, полученные в этих экспериментах, используют-ся при проектировании реальных объектов или коррекции их параметров.

Метод может дать достоверные результаты при соблюдении физического подобия реального явления и модели. Подобие достигается за счёт равенства модельных значений критериев подобия безразмерных чисел, зависящих от физических и геометрических параметров, характеризующих процесс исследования.
Экспериментальные данные, полученные методом физического моделирования распространяются на реальное явление также с учётом критериев подобия .
Недостаток физического моделирования заключается в том, что исключена возможность выполнения экспериментов в критических режимах (разрушение макета).

Некоторые примеры применения метода макетирочания (физического моделирования):
Исследование обтекания самолетов и автомобилей в аэродинамических трубах.
Гидродинамические исследования на уменьшенных моделях кораблей, гидротехнических сооружений .
Исследование сейсмоустойчивости зданий и сооружений на этапе проектирования.
Изучение устойчивости сложных конструкций, под воздействием разносторонних силовых нагрузок.
Измерение тепловых потоков и рассеивания тепла в устройствах и системах, работающих в условиях больших тепловых нагрузок.

Вопрос 12. Особенности математического моделирования технических систем
Математическое моделирование - это процесс замены технического объекта математическим объектом, называемого математической моделью. Исследование этой модели позволяет получить характеристики реального объекта. Вид математической модели зависит как от природы реального объекта, так от целей моделирования.
Математическое моделирование для исследования технических объектов использует совокупности формул, уравнений, неравенств определяющих структуру технической конструкции и описывающих ее поведение. Сложность и многообразие процессов функционирования реальных технических систем не позволяют строить для них абсолютно адекватные математические модели.
Математические модели технических систем функционируют посредством перехода из одного состояния в другое. Переход от состояния к состоянию осуществляется по детерминированным или вероятностным законам.

Одной из ветвей математического моделирования является аналитическое моделирование. Это математический формализованный процесс изменения свойств объекта во времени. Для такого способа моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраические, интегродифференцированные, конечно разностные) и логических условий. Такая модель может быть исследована 3-мя способами:
- аналитическим способом – когда необходимо получить в общем виде зависимость от исходных характеристик;
- численным способом – когда нельзя решить задачу в общем виде а получаем только результаты для конкретных начальных данных;
- качественным способом – когда не имея решения уравнения в общем виде, мы можем найти некоторые свойства решения.

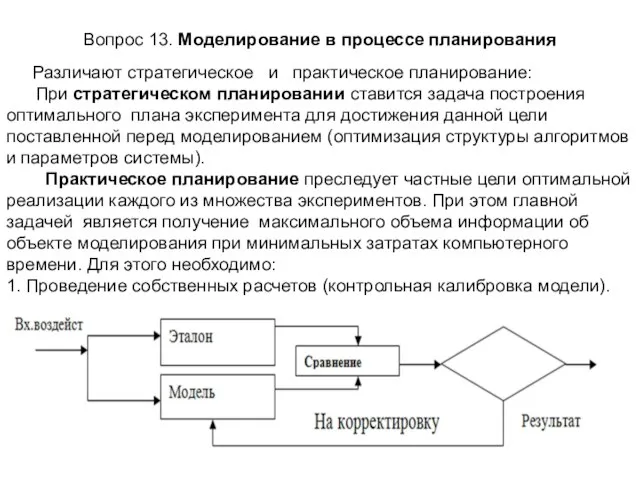
Вопрос 13. Моделирование в процессе планирования
Различают стратегическое и практическое планирование:
При стратегическом планировании ставится задача построения оптимального плана эксперимента для достижения данной цели поставленной перед моделированием (оптимизация структуры алгоритмов и параметров системы).
Практическое планирование преследует частные цели оптимальной реализации каждого из множества экспериментов. При этом главной задачей является получение максимального объема информации об объекте моделирования при минимальных затратах компьютерного времени. Для этого необходимо:
1. Проведение собственных расчетов (контрольная калибровка модели).

2.Статистическая обработка результатов расчетов и представление результатов в наглядной форме. Определение ошибок:
- формализации (модель недостаточно подробно определена)
- решения (применение упрощенного метода построения модели)
- некорректности ввода исходных данных.
3. Интерпретация результатов моделирования. Подведение итогов.
4. Составление технической документации.

Вопрос 14. Основные функции компьютера при моделировании систем
• выполнять роль вспомогательного средства для решения задач, решаемых обычными вычислительными средствами, алгоритмами, технологиями;
• выполнять роль средства постановки и решения новых задач, не решаемых традиционными средствами, алгоритмами, технологиями;
• выполнять роль средства конструирования компьютерных
обучающе - моделирующих сред;
• выполнять роль средства моделирования для получения новых знаний;
• выполнять роль "обучения" новых моделей (самообучающиеся модели).

Вопрос 15. Иерархические уровни при моделировании технических систем
Моделирование технических систем имеет иерархические уровни, различающиеся степенью детализации рассмотрения процессов.
Первый предусматривает описание объекта дифференциаль-ными уравнениями в частных производных, выражающих фундаментальные законы физики.
Второй уровень включает описание модели технического объекта системой обыкновенных дифференциальных уравнений с заданными начальными условиями. В их основе лежат уравнения элементов и уравнения межэлементных связей. С формальной точки зрения они имеют одинаковый вид для систем с различной физической природой, что явилось основанием для создания универсальных моделирующих комплексов.
Третий уровень - рассматривает модели большой сложности которые исследуются методами теории массового обслуживания и теории автоматического управления.

Вопрос №16
Основные этапы моделирования сложных технических систем
На первом этапе формулируется модель и строится её формальная схема. Основным назначением данного этапа является переход от содержательного описания объекта к его математической модели. Этот этап наиболее ответственный и наименее формализованный.
Последовательность действий:
Исследование моделируемого объекта с точки зрения выделения основных составляющих функционирования системы
Переход от содержательного описания модели к формализованному описанию свойств функционирования модели, т.е. к её концептуальной модели. Это сводится к исключению из рассмотре-ния некоторых второстепенных элементов, которые не оказывают существенного влияния на ход процесса исследуемой модели.

На втором этапе моделирования – этапе алгоритмизации и компьютерной реализации, математическая модель сформированная на
первом этапе воплощается в конкретную программную модель.
Последовательность действий следующая:
Разработка схемы моделирующего алгоритма.
Разработка схемы программы.
Выбор технических средств для реализации программной модели.
Процесс программирования и отладки.
Проверка достоверности программы на тестовых примерах.
Составление технической документации.
На 3-м этапе компьютер используется для проведения рабочих расчетов по готовой программе. Результаты этих расчетов позволяют проанализировать и сделать выводы о характеристиках процессов функционирования исследуемого объекта. Последовательность действий:
1. Планирование компьютерного эксперимента с моделью.
2. Составление плана проведения эксперимента с указанием комбинаций, переменных и параметров для которых должен проводится эксперимент.

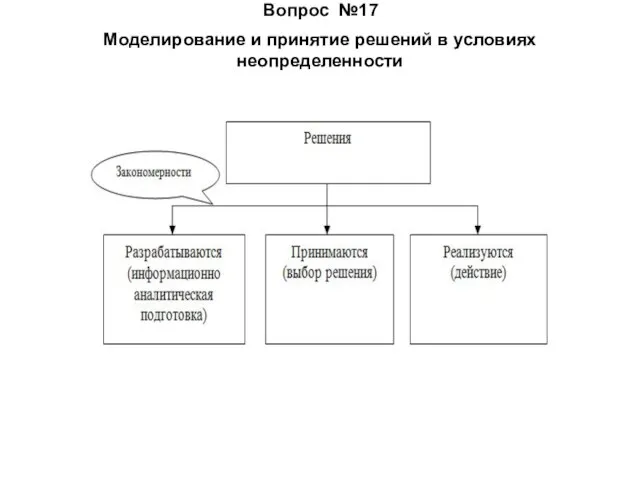
Моделирование и принятие решений в условиях неопределенности
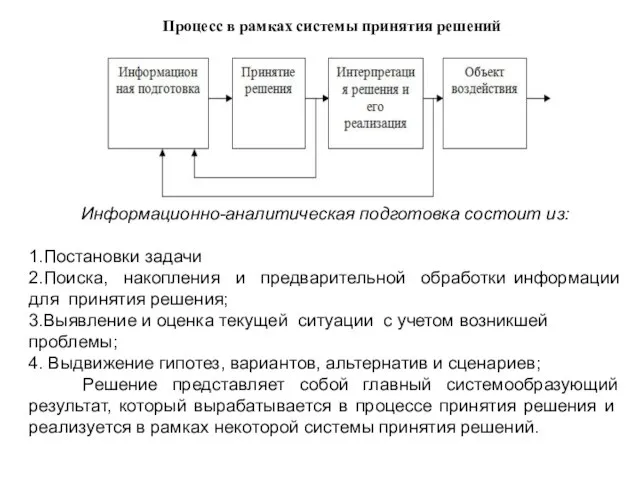
Вопрос №17

Процесс в рамках системы принятия решений
Информационно-аналитическая подготовка состоит из:
1.Постановки задачи
2.Поиска, накопления и предварительной обработки информации для принятия решения;
3.Выявление и оценка текущей ситуации с учетом возникшей проблемы;
4. Выдвижение гипотез, вариантов, альтернатив и сценариев;
Решение представляет собой главный системообразующий результат, который вырабатывается в процессе принятия решения и реализуется в рамках некоторой системы принятия решений.

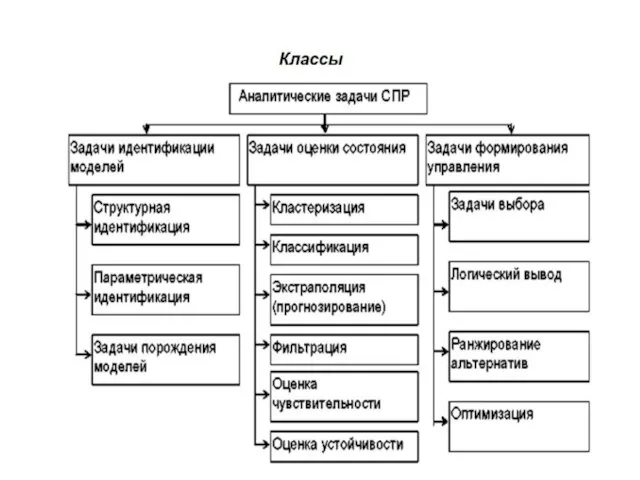
Вопрос № 18
Параметры и классы аналитических задач системы принятия решения (СПР)
Параметры
1. Пространство состояний объектов;
2. Множество характеристик, признаков, описывающих состояние объекта управления и принимающих свои значения в любом множестве;
3.Пространство управления (решений, проектов, планов);
4.Время (дискретное или непрерывное);
5. Пространство выходных значений (наблюдаемых проявлений и оценок);
6. Отображение динамики изменения состояния объекта, реакции динамической системы на управляющие воздействия;
7. Выходное отображение, описывающее процесс наблюдения объекта управления (получение оценок, мнений);
8. Внешние неуправляемые факторы, оказывающие влияние на динамику объекта управления.

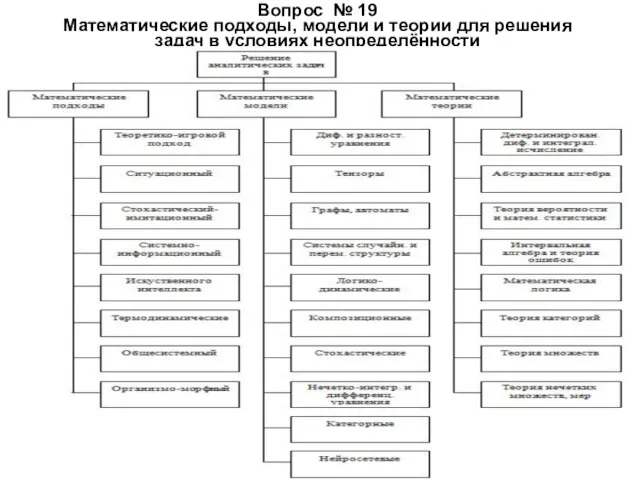
Вопрос № 19
Математические подходы, модели и теории для решения
задач в условиях неопределённости

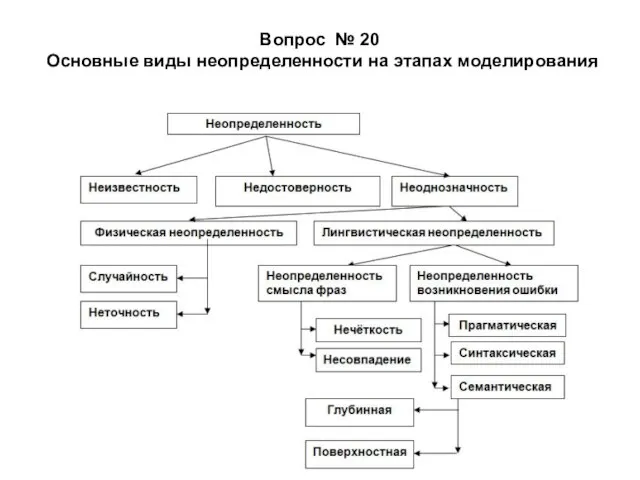
Вопрос № 20
Основные виды неопределенности на этапах моделирования

Вопрос 21. Математические теории предназначенные для фор-мализации неопределенной информации (данных):
Многозначная логика;
2. Теория вероятности;
3. Теория ошибок ;
4. Теория средних интервалов;
5. Теория субъективных вероятностей;
6. Теория нечетких множеств;
7. Теория нечетких мер и интегралов.

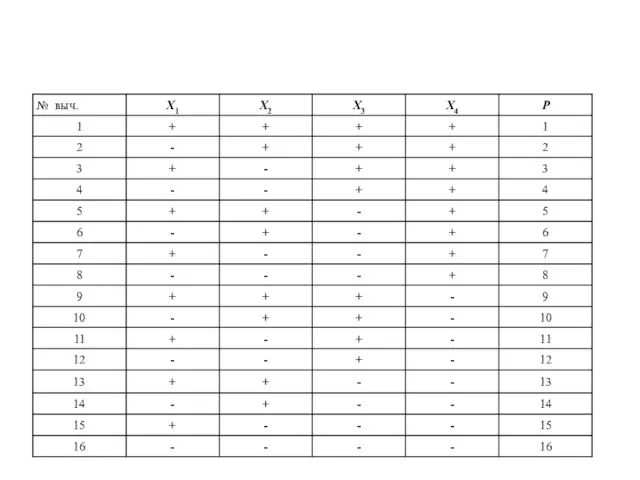
Вопрос № 22
Моделирование методом планирования эксперимента
После создания математической модели и её программной реализации важным этапом является постановка вычислительного эксперимента. В теории планирования эксперимента исследуемый объект рассматривается как черный ящик, имеющий входы X и выходы Y.
Х - входы Y – выходы
Переменные Х называются факторами, которые в эксперименте могут быть – качественными и количественными. Качественным факторам присваиваются числовые обозначения, тем самым осуществляется переход к количественным значениям. Переменные Х можно геометрически сопоставить с факторным пространством, координатные оси которого соответствуют значениям факторов. Совокупность значений факторов во всех точках плана эксперимента образует матрицу плана ПФЭ для n=4

Обрабатывая вектор результатов Р методом наименьших квадратов определяем вектор коэффициентов модели
Модель в общем виде для четырех факторов на двух уровнях имеет вид
Полученные коэффициенты будут характеризовать вес каждого фактора

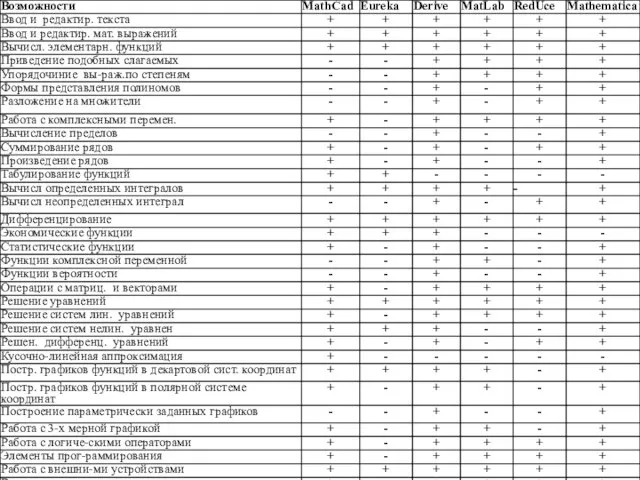
Вопрос № 23
Возможности основных комплексов математического моделирования динамических систем
Весь процесс математического моделирования невозможен без математических вычислений. Поэтому, математическое ядро каждого моделирующего динамические процессы комплекса имеет ряд возможностей для выполнения различных математических вычислений.

Вопрос № 24
Калькуляторные и решательные моделирующие комплексы
Большенство стандартных программных комплексов можно отнести к Мощным калькуляторам для статических вычислений и Специализированным решателям для моделирования динамических процессов.
Реализация калькуляторных и решательных программ предусматривает определение последовательности математических функций соответствующими вычислительными модулями. Однако в калькуляторных программах происходит однократное вычисление запланированной последовательности функций а в программах – решателях выполняется повторная последовательность вычислений в динамическом режиме работы технического устройства.
Каждая из программ математического моделирования динамических систем основана на одной из двух технологий:

Первая технология
Первая технология предполагает использование поточной модели управления при выполнении математических преобразований (функций) составляющих модель. Эти программы легко интегрируются с системами сбора данных, благодаря чему возможно создание (компьютерных) моделей с физическими объектами в контуре. В большинстве из них возможно программирование цифровых сигнальных процессоров. Структура их моделей может меняться согласно событийному управлению.

Вторая технология
Вторая технология предполагает представление модели в виде текстовой записи системы уравнений, которую решатели моделирующих программ обрабатывают в пакетном режиме. Эти программы, в скрытом от пользователя режиме, преобразуют текстовую запись систем уравнений к требуемому решателям виду. В этом случае с пользователя снимается задача подключения к модели итерационного решателя алгебраических уравнений. Эти особенности технологии позволили не ограничиваться моделями в виде передаточных функций. Они предоставляют пользователю возможность строить модели в виде технологических схем.
Главным затруднением для разработчиков моделирующих программ является графический интерфейс, который, должен быть полноценным редактором векторной графики.

Явный решатель моделирующей программы -это библиотека классических подпрограмм (функций), которые реализуют операцию интегрирования. (Дискретные квазианалоги интеграторов используются для решения дифференциальных уравнений).
Неявный (итерационный) решатель моделирующей программы -это библиотека классических подпрограмм, которые предназначены для решения алгебраических уравнений путем итерационного подбора независимых переменных.
Оптимизирующий решатель моделирующей программы -это разновидность неявного решателя, которая предназначена для минимизации значения функции в процессе итерационного подбора ее независимых переменных.

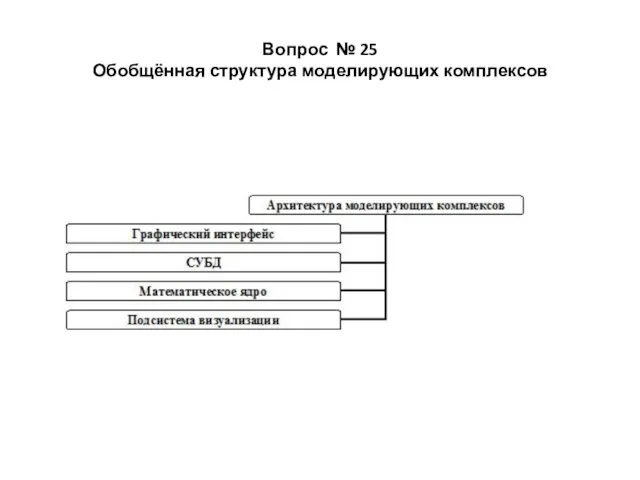
Вопрос № 25
Обобщённая структура моделирующих комплексов

Графический интерфейс отвечает за представление математической модели в виде, понятном широкому кругу специалистов. Это могут быть блок-схемы, схемы физические принципиальные, гибридные карты состояний и пр.
СУБД отвечает за хранение исходных, промежуточных и итоговых данных составленной пользователем модели и осуществляет управляемую трансформацию структуры хранилища данных.
Математическое ядро осуществляет основную вычислительную нагрузку, и в цикле, согласно заданной программе, обеспечивает исполнение потоков математических функций.
Подсистема визуализации обеспечивает интерфейс между функционирующим математическим ядром и пользователем.

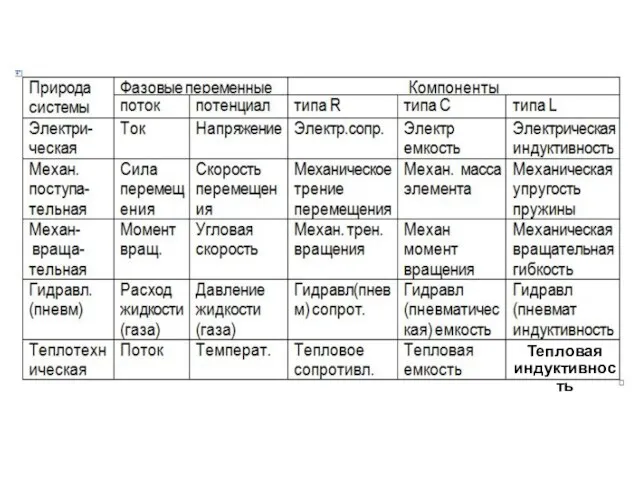
Вопрос № 26
Компонентные и топологические уравнения для моделирования технических систем методом эквивалентных схем.
Компонентные уравнения отражают законы функционирования элементов. Они формируются на основе знаний о конкретной предметной области. Связь между элементами осуществляется топологическими уравнениями.
Формы Компонентных и Топологических уравнений для объектов различной физической природы одинаковы.
В большинстве технических систем можно выделить три типа простейших элементов R, С, L . В первом элементе R происходит преобразование кинетической и потенциальной энергии в тепловую. Элементы С и L накапливают потенциальную или кинетическую энергию. Сочетанием этих элементов и источников сигналов получаем ММ любой сложности. Таким образом, существующие аналогии между переменными параметрами в системах различной физической природы сведены в таблицу:

Тепловая
индуктивность

Вопрос № 27

Вопрос № 28

Вопрос № 29

Вопрос № 30

3) Уравнение теплоиндуктивности:
Т=LT(dФT/dt); где LT - тепловая индуктивность
Вопрос № 31

Вопрос № 32

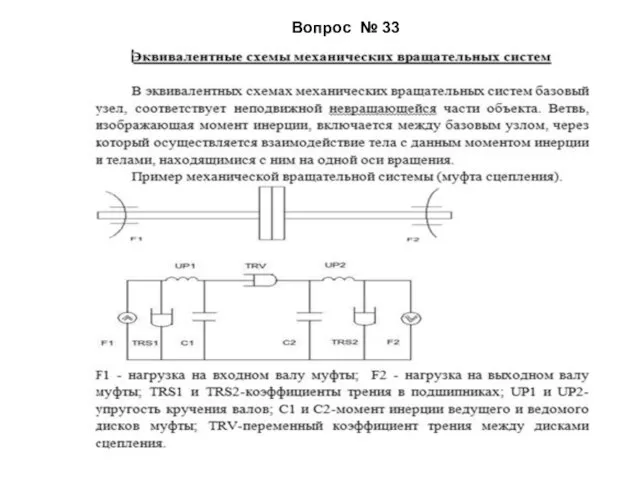
Вопрос № 33

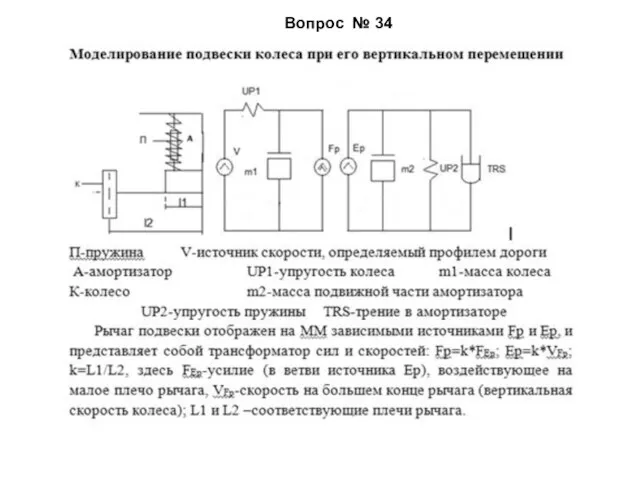
Вопрос № 34

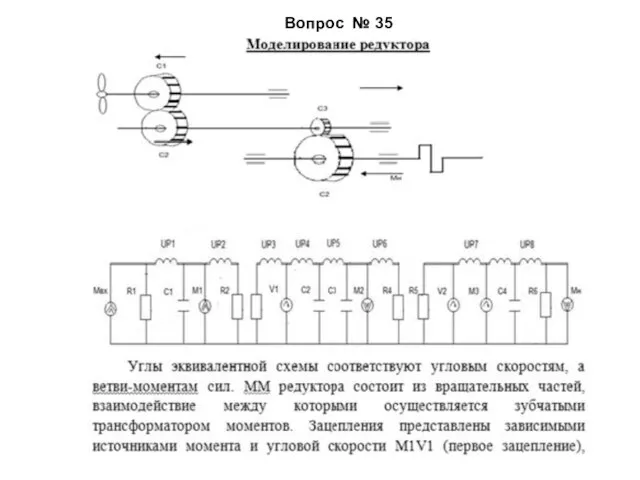
Вопрос № 35

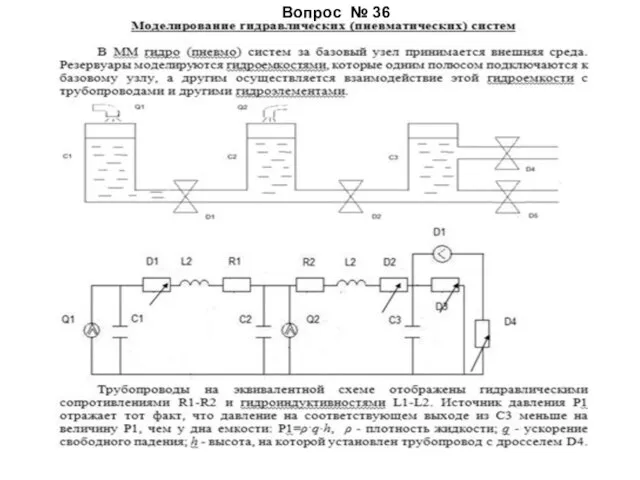
Вопрос № 36

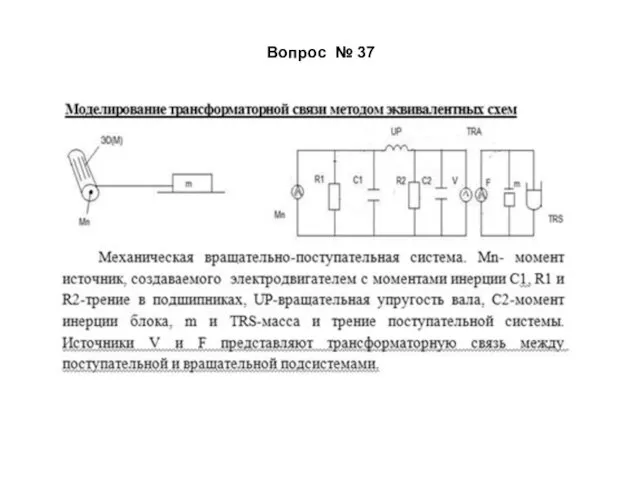
Вопрос № 37

Вопрос № 38

сооружениях отпадает
Вопрос № 39

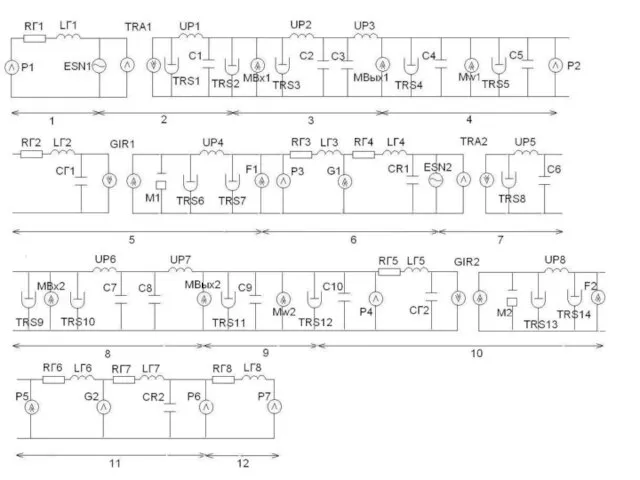
1 – Модель водозаборного устройства;
2 - Модель электрогенератора первого уровня;
3. – Модель электродвигателя первого уровня;
4 - Модель зубчато-червячной передачи первого уровня;
5 – Модель поршневого насоса первого уровня;
6 – Модель сборного резервуара;
7 – Модель электрогенератора второго уровня;
8 - Модель электродвигателя второго уровня;
9 - Модель зубчато-червячной передачи второго уровня;
10 - Модель поршневого насоса второго уровня;
11 – Модель напорной регулирующей ёмкости;
12 – Модель трубопровода к потребителю

Rг1, Lг1 – Rг8, Lг8 – модели трубопроводов
Esn1,2 – источники синусоидального напряжения дизель – генераторов.
TRA1,2 – трансформаторная связь электрической части дизель-генераторов и их механических вращающихся частей.
TRS1,8 – коэффициенты трения в подшипниках дизель – генераторов.
UP1,5 – крутильные гибкости ведомых валов дизельных – генераторов.
C1,6 – моменты инерции ведомых валов дизельных – генераторов.
TRS2,9 – коэффициенты трения муфт ведомых валов генераторов и входных валов двигателей.
Mвх1,2 – моменты на ведущих валах двигателей.
TRS3.10 – коэффициенты трения в подшипниках ведущих валов.
UP2,6 – крутильные гибкости ведущих валов двигателей.
C2,7 - моменты инерции ведущих валов двигателей.
C3,8 - моменты инерции ведомых валов двигателей.
UP3,7- крутильные гибкости ведомых валов.
Mвых1,2 – моменты на выходе валов.
TRS4,11 - коэффициенты трения первых зубчатых и червячных зацеплений.
C4,9 – моменты инерции первых зубчатых и червячных зацеплений.

Mω1,2 – моменты противодействия вращению первых зубчатых колёс со стороны вторых.
TRS5,12 - коэффициенты трения вторых зубчатых и червячных зацеплений.
C5,10 - моменты инерции вторых зубчатых и червячных зацеплений.
P1,2,3,4,5,6 ,7– источники давления.
Cг1,2 – гидроёмкости цилиндров насосов.
GIR1,2 – гираторные связи.
M1,2 – массы поршней.
TRS6,13 – трение поршней о стенки цилиндров насосов.
UP4,8 – упругости истоков поршней насосов.
TRS7,14 – трение штоков о пазы цилиндров насосов.
F1,2 – усилия действующие на штоки насосов.
G1,2 – источники расхода жидкости.
CR1,R2 – ёмкости сборного и регулирующего резервуаров.

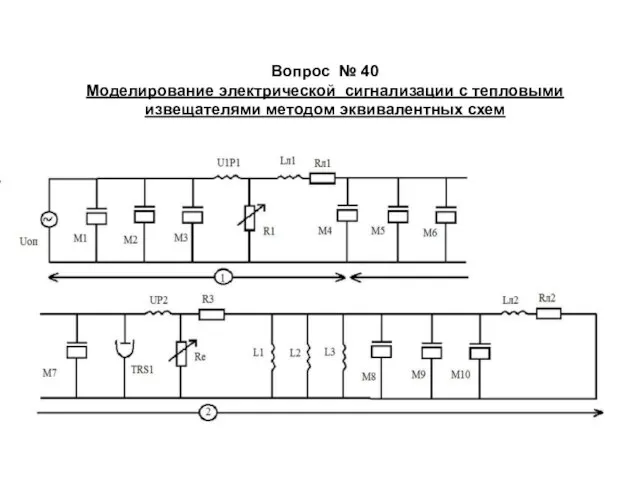
Вопрос № 40
Моделирование электрической сигнализации с тепловыми извещателями методом эквивалентных схем

1. Модель электроиагнитного реле; 2. Модель теплового извещателя.
Где:
Uоп. – напряжение основного источника питания
М1 – масса электромагнита с катушкой реле
М2 – масса ферромагнитного якоря реле
М3 – масса золотника клапана реле
UP1 – пружина для настройки хода якоря и золотника реле
R1- переключающий контакт
Lл1, Rл1 – модель сигнальной лампы
M4 – масса плавкой вставки извещателя
M5 – масса штольневой трубки извещателя
M6 – масса резьбовой крышки извещателя
M7 – масса штока упирающегося во вставку извещателя
TRS1 – трение при перемещении штока
UP2 – пружина для замыкания контакта R2 извещателя
R2 – переключающийся контакт извещателя
R3 – шунтирующий резистор
L1 – L3 – катушки лучевых реле
М8 – М10 – массы элементов дымозасасывающих трубок
Lл2, Rл2 – модель звена световой сигнализации

Вопрос № 41
Моделирование систем методом искусственного интеллекта
Повышение интеллектуальности подсистем моделирования и проектирования осуществляется путем использования эвристического программирования экспертных систем, путем перехода от режима диалога к пакетному режиму.
Существует несколько проблем искусственного интеллекта возникающих на этапах моделирования и проектирования.
Представление знаний — разработка методов и приемов для формализации и последующего ввода в память интеллектуальной системы знаний из различных проблемных областей,
Обобщение и классификация накопленных знаний, применение знаний при решении задач.

Моделирование рассуждений — изучение и формализация различных схем человеческих умозаключений, используемых в процессе решения разнообразных задач, создание эффективных программ для реализации этих схем в вычислительных машинах.
Диалоговые процедуры общения на естественном языке, обеспечивающие контакт между интеллектуальной системой и человеком-специалистом в процессе решения задач.
Планирование целесообразной деятельности — разработка методов построения программ сложной деятельности на основании тех знаний о проблемной области, которые хранятся в интеллектуальной системе.
Обучение интеллектуальных систем в процессе их деятельности, создание комплекса средств для накопления и обобщения умений и навыков, накапливаемых в таких системах.

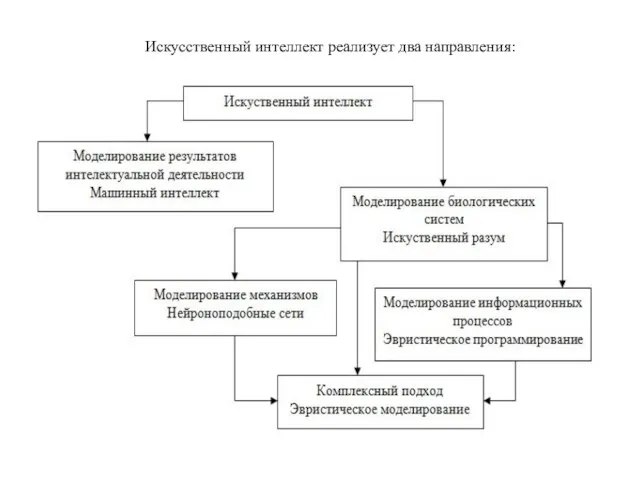
Искусственный интеллект реализует два направления:

Вопрос № 42
Основы моделирования процессов методом кле́точного автома́та
Клеточный автомат это дискретная модель которая включает регулярную решётку ячеек, каждая из которых может находится в одном из конечного множества состояний, таких как 0 и 1. Решетка может быть любой размерности. Для каждой ячейки определено множество ячеек, называемых соседством. Для работы клеточного автомата требуется задание начального состояния всех ячеек, и правил перехода ячеек из одного состояния в другое. На каждой итерации, используя правила перехода и состояния соседних ячеек, определяется новое состояние каждой ячейки. Обычно правила перехода одинаковы для всех ячеек и применяются сразу ко всей решётке.

Основное направление исследования клеточных автоматов — алгоритмическая разрешимость тех или иных проблем. Также рассматриваются вопросы построения начальных состояний, при которых клеточный автомат будет решать заданную задачу.
Модели на основе клеточных автоматов представляют собой одну из ветвей имитационного моделирования. Они представляют собой алгоритм функционирования системы, который не имеет аналога в виде математической модели, так что динамика изменения состояния такого автомата может быть исследована только путем модельного эксперимента, и заранее предсказать закономерности его развития невозможно.

Модельным клеточным автоматом называется сеть из дискретных клеток, меняющих свое состояние в дискретные моменты времени. Чаще всего рассматриваются двумерные клеточные автоматы, элементами которых являются квадратные клетки (впрочем, форма клеток может быть и иной — треугольник, шестиугольник и т. д.). Каждая клетка может находиться в одном из конечного числа состояний, а время в данной модели представлено дискретным множеством тактов. Состояние каждой клетки автомата в последующий момент времени определяется ее собственным состоянием и состоянием ближайших соседей в предыдущий момент. Среда предполагается однородной, т. е. правила изменения состояний для всех клеток одинаковы. Если эти правила зависят от случайных факторов, то автомат называется стохастическим; в противном случае — детерминированным.
С помощью клеточных автоматов целесообразно моделировать такие сложные процессы, как самоорганизация технических систем, турбулентность и социальные процессы. Результаты моделирования на основе клеточных автоматов имеют простую наглядную графическую форму отображения.

Вопрос № 43
Моделирование разветвленных технических систем
Разветвленными системами считаются крупные технологические, производственные, энергетические, коммуникационные комплексы, системы управления, социальные, экономические, экологические системы и т. п., которые могут быть искусственного или естественного происхождения.
Разветвленные системы характеризуются большим количеством элементов и связей, разнообразием взаимодействий между системой и окружающей средой, наличием случайных факторов внутренней и внешней природы, возможностью случайного изменения структуры.
Обычно выделяют структурную и поведенческую сложность моделируемых объектов.
Для систем сложного поведения характерно несколько качественно различных, последовательно сменяющих друг друга во времени режимов функционирования. Подобная сложная динамическая система в каждый конкретный момент времени ведет себя как некоторая относительно простая динамическая система, однако при определенных условиях режим ее функционирования скачкообразно меняется. Например, гидротехническое сооружение с двумя трубами обладает сложным поведением, поскольку его поведение при переполнении качественно отличается от его поведения при нормальном уровне воды или при опорожнении.

К основным функциям разветвленных систем относятся:
1. Такие модели систем помогают упорядочить представления о свойствах этих систем. В технике такие модели служат в качестве средства для создания новых, более совершенных систем.
2. Такие модели систем применяются как средство для обучения лиц, которые должны уметь справляться со всевозможными случайностями до возникновения критической ситуации (модели космических кораблей, тренажеры для обучения водителей, операторов АЭС и др.).
3. Одним из важных применений моделей разветвленных систем является прогнозирование поведения моделируемых объектов и диагностика их состояния.
4. Модели разветвленных систем позволяют производить контролируемые эксперименты в ситуациях, когда экспериментирование на реальных объектах экономически нецелесообразно, опасно или практически невозможно.

Естественно, что при исследовании сложной системы, содержащей большое количество элементов, невозможно детально моделировать процессы в каждом элементе. С общесистемной точки зрения представляют интерес только те свойства элементов, которые непосредственно влияют на свойства системы в целом.
Модельное исследование разветвленных динамических систем выполняется на основе пакетов визуального моделирования , которые позволяют вводить описание моделируемой системы в естественной для прикладных наук форме. Имеется возможность рисовать функциональную схему, размещать на ней блоки различного рода факторов, в том числе случайных, и прослеживать их влияние. Детальные компьютерные эксперименты с моделью системы позволяют лучше понять законы ее функционирования и разработать предложения по ее улучшению, которые были бы невозможны без имитации.
Имитация разветвленных систем дает представление о наиболее существенных факторах, определяющих ее свойства, позволяет исследовать новые ситуации, которые ранее были неизвестны, и провести предварительную проверку различных стратегий принятия решений перед проведением экспериментов на реальной системе, позволяет экспериментально исследовать сложные внутренние взаимодействия в системе, будь то отрасль, отдельная фирма или экономика в целом.

Вопрос № 44
Моделирование стохастических процессов.
Моделирование случайных (стохастических) процессов — это одно из важнейших направлений имитационного моделирования. Событие называется случайным, если оно достоверно непредсказуемо..
В практике моделирования это экономические, социальные, экологические, производственные и любые другие системы, в которых значительную роль играет человеческий фактор.
В задаче оптимального размещения ресурсов предполагается, что для всех ее параметров известны точные значения, или, иными словами, все параметры такой задачи считаются детерминированными. Однако на практике точных значений этих параметров просто не существует. Действительно, при выполнении любой работы могут быть непредсказуемые перебои с поставками сырья; цены на рынке подвержены колебаниям и т. п. Все эти факторы имеют случайный характер, и говорить об их конкретных значениях можно только с определенной вероятностью.
При моделировании случайных процессов значительно изменя­ется сама методология моделирования — основными методами изу­чения подобных систем становятся стохастическое моделирование и статистическая обработка его результатов.

В целом стохастическое моделирование — это метод получения с помощью компьютера статистических данных о процессах, происходящих в моделируемой системе, параметры которой изменяются случайным образом с заданным законом распределения. Сущность метода стохастического моделирования сводится к построению моделирующего алгоритма, имитирующего функционирование системы, случайные воздействия на систему, случайные изменения параметров системы и случайные изменения начальных условий. Такой алгоритм многократно реализуется с помощью компьютерных программных средств, в результате чего получается серия частных значений искомых величин, статистическая обработка которых позволяет получить информацию о свойствах системы. Если количество таких реализаций велико, то по­лученные результаты с достаточной точностью могут характеризовать процесс функционирования системы. В ходе модельных экспериментов с помощью имитационной модели воспроизводится влияние случайных факторов. При этом, для получения статистических данных о свойствах объекта или про-цесса требуется его многократное воспроизведение в ходе моделирования.
Первоначально подобный метод был разработан и применялся для решения детерминированных аналитических задач, получив название метода Монте-Карло. Согласно ему детерминированная вычислительная задача заменяется эквивалентной схемой некоторой стохастической системы, выходные характеристики которой совпадают с результатом решения этой задачи.

Вопрос № 45
Моделирование виртуальных приборов средствами LabVIEW
LabVIEW – среда разработки прикладных программ, использующая специфический язык графического программирования и не требующей написания текстов программ.
Среда программирования, LabVIEW имеет библиотеки функций и подпрограмм для приема данных, их анализа и обработки. Реализации программ LabVIEW называются виртуальными инструментами, поскольку их внешнее графическое представление и способ функционирования имитируют работу реальных физических приборов. Виртуальные инструменты имеют интерактивный интерфейс пользователя, представленный в виде передней панели, аналогичной панели реального физического прибора и содержащей ручки управления, кнопки, графические индикаторы и другие средства управления и индикации. Источником кода виртуального инструмента служит блок-схема, отображающая графическое представление программируемой задачи.
Программная реализация виртуальных инструментов использует в своей работе принципы иерархичности и модульности. Виртуальный инструмент, содержащийся в составе другого виртуального инструмента, называется прибором-подпрограммой. Данный комплекс способен моделировать сложные технические измерительные приборы.

Вопрос № 46
Основы моделирования методом конечных элементов
Метод конечных элементов (МКЭ) — численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравненний, возникающих при решении задач прикладной физики. Метод широко используется для решения задач деформации тел, теплообмена, гидравлики и электродинамики.
Суть метода следует из его названия. Область, в которой ищется решение, разбивается на конечное количество подобластей (элементов). В каждом из элементов произвольно выбирается вид функции. Вне своего элемента функция равна нулю. Значения функций на границах элементов (узлах) является решением задачи и заранее неизвестно. Коэффициенты функций обычно ищутся из условия равенства значения соседних функций на границах между элементами (в узлах). Затем эти коэффициенты выражаются через значения функций в узлах элементов. Составляется система линейных алгебраических уравнений. Количество уравнений равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы, прямо пропорционально количеству элементов. Так как каждый из элементов связан с ограниченным количеством соседних, система линейных алгебраических уравнений имеет разряжённый вид, что существенно упрощает её решение.

С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти, для численного анализа системы позволяет рассматривать его как одну из конкретных ветвей информационного дерева — путём его расчленения.
Наиболее полно метод реализуется в моделирующем комплексе ELCUT. Он проволяет моделировать электромагнитные, тепловые и механических процесссы:
– Линейная и нелинейная магнитостатика.
– Магнитное поле переменных токов (с учетом вихревых токов).
– Нестационарное магнитное поле.
– Электростатика.
– Электрическое поле переменных токов в неидеальном диэлектрике.
– Растекание токов в проводящей среде.
– Линейная и нелинейная, стационарная и нестационарная теплопередача.
– Линейный анализ напряженно-деформированного состояния.
– Связанные задачи.

Вопрос № 47
Функциональное моделирование систем
Функциональное моделирование применяется для анализа функциональных схем при их проектировании. Процедура проектирования последних соответствует общей схеме функционального блока. Целью их анализа является проверка правильности функционирования системы на данном этапе ее разработки.
Математические модели функциональных схем должны быть более простыми, чем полные математические модели, получаемые методами схемотехнического проектирования. Для технических агрегатов используются два подхода к синтезу математической модели функциональных схем.

Первый подход основан на макромоделировании. Модели элементов в этом случае соответствуют упрощенным эквивалентным схемам этих элементов. Объединение моделей элементов в общую модель технического устройства выполняется с помощью метода переменных состояний или узлового метода. Трудности такого подхода заключаются в том, что отсутствуют формализованные методики получения технических макромоделей, а также в сравнительно большой размерности получаемых систем уравнений.
Второй подход базируется на использовании функционального моделирования. Модели элементов систем представляются в виде передаточных функций, являющиеся носителями информации ( сигналы). Объединение моделей элементов в модель системы осуществляется на основе отождествления входных и выходных сигналов, соответствующих соединяемым входам и выходам элементов.

Вопрос № 48
Моделирование режимов работы станков с числовым программным управлением
Процесс моделирования режимов обработки на станках с ЧПУ связан с разработкой управляющих программ. Программирование обработки в основном осуществляется на языке G и М кодов. Коды с адресом G, называемые подготовительными и определяют настройку СЧПУ на определенный вид работы. Коды с адресом М называются вспомогательными и предназначены для управления режи­мами работы станка.
Для управления многочисленными функциями станка с ЧПУ применя­ется довольно большое число различных кодов. Рассмотрим некоторые коды.

Программно увязав несколько станков с
ЧПУ в гибкую автоматизированную производственную систему, можно сформировать гибкий автоматизированный участок и войти в состав автоматической линии производства участка либо цеха.

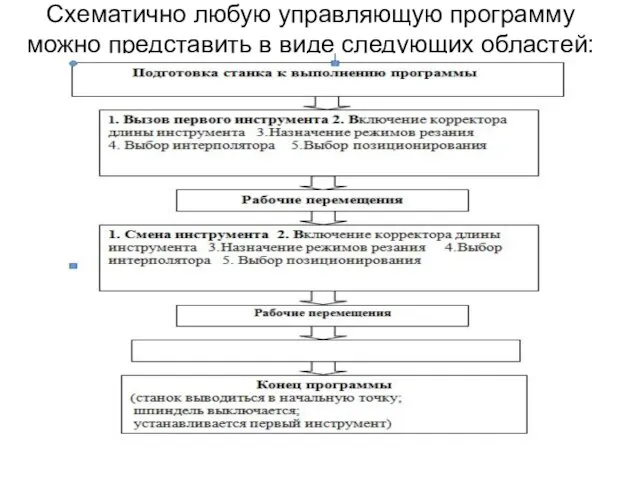
Схематично любую управляющую программу можно представить в виде следующих областей:

Вопрос № 49 Назначение и возможности САПР
Основная цель создания САПР - повышение эффективности труда инженеров:
Сокращение трудоёмкости проектирования и планирования;
Сокращение сроков проектирования;
Сокращение себестоимости проектирования и изготовления, уменьшение затрат на эксплуатацию;
Повышение технико-экономического уровня результатов проектирования;
Сокращение затрат на натурное моделирование и испытания.
Достижение этих целей обеспечивается путем:
Автоматизации оформления документации;
Информационной поддержки и автоматизации процесса принятия решений;
Использования технологий параллельного проектирования;
Унификации проектных решений и процессов проектирования;
Повторного использования проектных решений, данных и наработок;
Стратегического проектирования;
Замены натурных испытаний и макетирования математическим моделированием;
Повышения качества управления проектированием;
Применения методов вариантного проектирования и оптимизации.
Визуализация результатов моделирования столкновения выполненная с использованием метода конечных элементов.

Вопрос № 50
Состав и структура САПР
Составными структурными частями САПР являются:
Обслуживающие подсистемы —обеспечивают функционирование проектирующих подсистем, оформление, передачу и вывод данных, сопровождение программного обеспечения (системная среда).
Проектирующие подсистемы —реализуют определенный этап проектирования или группу связанных проектных задач. Они делятся на:
- объектные — выполняющие проектные процедуры и операции, связанные с конкретным типом объектов проектирования.
- инвариантные — выполняющие унифицированные
проектные процедуры и операции.
Типичными обслуживающими подсистемами являются:
Подсистемы управления проектными данными
Обучающие подсистемы для освоения пользователями технологий, реализованных в САПР
Подсистемы графического ввода-вывода
СУБД.

Вопрос № 51
Компоненты и обеспечение САПР.
Каждая подсистема состоит из компонентов, обеспечивающих функционирование подсистемы. Компонент выполняет определенную функцию в подсистеме и представляет собой наименьший (неделимый) самостоятельно разрабатываемый или покупной элемент САПР Совокупность однотипных компонентов образует средство обеспечения САПР. Выделяют следующие виды обеспечения САПР:
Техническое обеспечение (ТО) — совокупность связанных и взаимодействующих технических средств (ЭВМ, сетевое и периферийное оборудование, линии связи, измерительные средства).
Математическое обеспечение (МО), объединяющее математические методы, модели и алгоритмы, используемые для решения задач автоматизированного проектирования. По назначению и способам реализации делят на две части:
математические методы и построенные на них ММ;
формализованное описание технологии автоматиз. проектирования.
Программное обеспечение (ПО) подразделяется на общесистемное и прикладное:

Общесистемное ПО предназначено для управления компонентами технического обеспечения и обеспечения функционирования прикладных программ. Примером компонента общесистемного ПО является операционные системы.
Информационное обеспечение (ИО) — совокупность сведений, необходимых для выполнения проектирования. Состоит из описания стандартных проектных процедур, типовых проектных решений, комплектующих изделий и их моделей, правил и норм проектирования. Основная часть ИО САПР — база данных.
Прикладное ПО обеспечение реализует математическое обеспечение для непосредственного выполнения проектных процедур. Включает пакеты прикладных программ, предназначенные для обслуживания определенных этапов проектирования или решения групп однотипных задач внутри различных этапов (модуль проектирования трубопроводов, пакет схемотехнического моделирования, геометрический решатель САПР).

Лингвистическое обеспечение (ЛО) — совокупность языков, используемых в САПР для представления информации о проектируемых объектах, процессе и средствах проектирования, а также для осуществления диалога проектировщик-ЭВМ и обмена данными между техническими средствами САПР. Включает термины, определения, правила формализации естественного языка, методы сжатия и развертывания.
Методическое обеспечение (МетО) — описание технологии функционирования САПР, методов выбора и применения пользователями технологических приемов для получения конкретных результатов. Включает в себя теорию процессов, происходящих в проектируемых объектах, методы анализа, синтеза систем и их составных частей, различные методики проектирования. Иногда к МетО относят также МО и ЛО.
Организационное обеспечение(ОО) — совокупность документов, определяющих состав проектной организации, связь между подразделениями, организационную структуру объекта и системы автоматизации, деятельность в условиях функционирования системы, форму представления результатов проектирования… В ОО входят щтатные распсания, должносные инструкции, правила эксплуатации, приказы, положения и т. п.
Эргономическое обеспечение объединяет взаимосвязанные требования, направленные на согласование психологических, психофизиологических, антропо-метрических характеристик и возможностей человека с техническими характеристиками средств автоматизации и параметрами рабочей среды на рабочем месте.
Правовое обеспечение состоит из правовых норм, регламентирующих правоотношения при функционировании САПР, и юридический статус результатов ее функционирования.