Содержание
- 2. Арифметическая прогрессия
- 3. Закончился двадцатый век. Куда стремится человек? Изучены космос и море, Строенье звезд и вся Земля. Но
- 4. Из истории Арифметической прогрессии
- 5. Древний Египет, страна великих достижений человеческой мысли, великих астрономов и математиков. Самый большой, сохранившийся до наших
- 6. «Тебе сказано: раздели 10 мер хлеба на 10 человек, если разность между каждым человеком и следующим
- 7. Фигурные числа Фигурные числа были известны еще в Древнем Вавилоне. В V - IV веках до
- 8. d=1 1;2;3;4;… d=3 1;4;7;10;… d=2 1;3;5;7;…
- 9. Формула суммы первых n членов арифметической прогрессии Sn в истории выводилась неоднократно и разными способами. Способ
- 10. С формулой связан один из эпизодов биографии К.Ф.Гаусса. В дальнейшем Гаусс сделал много замечательных открытий. Его
- 11. Древнейшая задача о делении хлеба Сто мер хлеба разделить между пятью людьми так, чтобы второй получил
- 12. Следовательно, хлеб должен быть разделен на следующие части:
- 13. Индийский астроном и математик Ариабхата (V в.) применял формулы общего числа, суммы n членов арифметической прогрессии.
- 14. Арифметическая прогрессия Последовательность, в которой каждый член, начиная со второго равен предыдущему, сложенному с одним и
- 15. 1) 2; 5; 8; 11;14; 17;… 2) 3; 9; 27; 81; 243;… 3) 1; 6; 11;
- 16. Формула n-го члена арифметической прогрессии an=a1+d(n-1) Дано: a1 = 7, d = 5 Найти: a4 a4=22
- 17. Арифметическая прогрессия Каждый член последовательности начиная со второго есть среднее арифметическое между предыдущим и последующим членами
- 18. Формулы суммы n первых членов прогрессий Дано: a1 = 5, d = 4 Найти: S5 S5
- 19. 1. Про арифметическую прогрессию (аn) известно, что а7 = 8, а8 = 12. найдите разность арифметической
- 20. За 16 дней Карл украл у Клары 472 коралла. Каждый день он крал на 3 коралла
- 21. 1.Решение: S16=½ (2∙а1 + 3∙15) ∙16; 472 =16 а1 + 360; а1 = (472- 360):16=7. а16
- 22. В сборнике по подготовке к экзамену 240 задач. Ученик планирует начать их решение 2 мая, а
- 23. 2.Решение: 240=½(2 а1 +2 ∙14) ∙ 15; 240:15= а1 + 14; а1 = 2; а11= 2+2
- 24. В амфитеатре расположены 10 рядов, причем в каждом следующем ряду на 20 мест больше чем в
- 25. 3.Решение: 280= а1 + 20∙(10-1); а1= 280 - 20 ∙ 9 = 100; S10 = ½(100+280)
- 26. Тест по теме «Арифметическая прогрессия» Пройдите за компьютеры. У вас 15 минут. Успешного решения!
- 27. Домашнее задание На «4» Сборник ГИА Кузнецова Л.В. №7.19-7.21 (2) На «5» Сборник ГИА Кузнецова Л.В.
- 28. Оцените свои знания и умения на конец урока. Был ли полезен урок для каждого из вас?
- 29. Урок сегодня завершён, Дружней вас не сыскать. Но каждый должен знать: Познание, упорство, труд К прогрессу
- 30. I (слайд 2 ) Тему сегодняшнего урока мы узнаем, разгадав кроссворд: 1. Как называется график квадратичной
- 32. Скачать презентацию










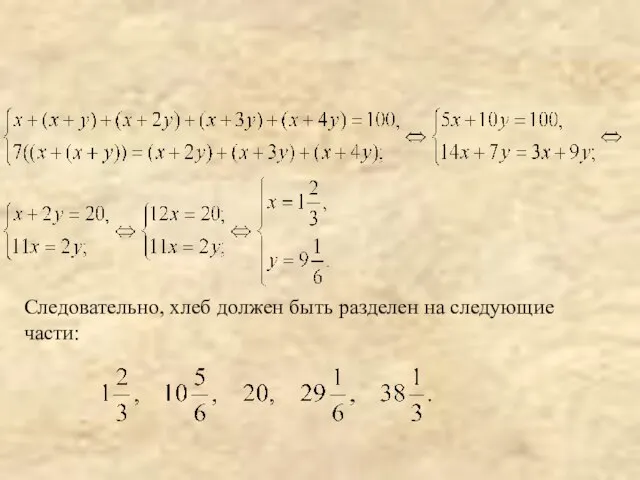


















 Положение о системе общественного наблюдения при проведении государственной (итоговой) аттестации обучающихся, освоивших образ
Положение о системе общественного наблюдения при проведении государственной (итоговой) аттестации обучающихся, освоивших образ Употребление многозначных глаголов в речи (6 класс)
Употребление многозначных глаголов в речи (6 класс) Методический материал к уроку русского языка в 6 классе на тему: «Фразеологизмы».
Методический материал к уроку русского языка в 6 классе на тему: «Фразеологизмы». Западная философия 20-го века
Западная философия 20-го века Лот 5, г. Хабаровск, ул. Сысоева, 21, кв. 14
Лот 5, г. Хабаровск, ул. Сысоева, 21, кв. 14 Барометрия. Задачи барометрии
Барометрия. Задачи барометрии Прямоугольный параллелепипед. Куб (5 класс)
Прямоугольный параллелепипед. Куб (5 класс) Образ современного подростка в произведениях А. Иванова «Географ глобус пропил» и «Общага-на-крови»
Образ современного подростка в произведениях А. Иванова «Географ глобус пропил» и «Общага-на-крови» Финансовая компания Автомайн
Финансовая компания Автомайн Энциклопедия термина число
Энциклопедия термина число Своя игра
Своя игра Формування системи документування господарських операцій та документообігу (Тема №6). Організація документообігу на підприємстві (Лекція
Формування системи документування господарських операцій та документообігу (Тема №6). Організація документообігу на підприємстві (Лекція Лекция №2
Лекция №2 Розроблення технології пасти із насінням соняшника з підвищеною біологічною цінністю для людей конституції типу Пітта-Доша
Розроблення технології пасти із насінням соняшника з підвищеною біологічною цінністю для людей конституції типу Пітта-Доша Удельное сопротивление
Удельное сопротивление Народная сказка: история происхождения и её герои
Народная сказка: история происхождения и её герои Описание рекламных мест
Описание рекламных мест Типология организационных культур Герта Хофстеда
Типология организационных культур Герта Хофстеда Общая физическая подготовка на занятиях по волейболу
Общая физическая подготовка на занятиях по волейболу Значение мяса в питании человека. Виды мяса. Требования к качеству
Значение мяса в питании человека. Виды мяса. Требования к качеству КАСКО – Профи
КАСКО – Профи Socialization
Socialization Презентация по обществознанию
Презентация по обществознанию Формирование функции голосообразования у младших школьников в условиях школы второго вида
Формирование функции голосообразования у младших школьников в условиях школы второго вида Общая схема МЭМС. МЭМС с 3-х аксиальными гироскопами и акселерометрами различных компаний
Общая схема МЭМС. МЭМС с 3-х аксиальными гироскопами и акселерометрами различных компаний Зарядка для глаз
Зарядка для глаз Модель внимания Сергея Леонидовича Рубинштейна
Модель внимания Сергея Леонидовича Рубинштейна Проблемы экологии в России и Великобритании в 21 веке Андрианова Н.Г.
Проблемы экологии в России и Великобритании в 21 веке Андрианова Н.Г.