Слайд 2Часть 1. Основы теории линейных непрерывных САУ.
1.1. Математические модели САУ. 3-37
1.2.

Типовые звенья САУ и их характеристики. 38-56
1.3. Преобразование структурных схем САУ. 57-71
1.4. Передаточные функции замкнутых САУ. 72-75
Слайд 5 Для описания математической модели САУ обычно используется три способа:
1) поэлементное описание САУ

с учётом взаимодействия каждого звена с другими звеньями и с внешней средой. При этом модель САУ описывают системой дифференциальных уравнений, учитывающих все параметры звеньев, входные и выходные величины (координаты) процессов управления, что обеспечивает возможность физической интерпретации всех процессов управления;
Слайд 6 Для описания математической модели САУ обычно используется три способа:
2) системное описание САУ

представляется одним уравнением, которое получается из поэлементного описания САУ методом подстановок для исключения промежуточных координат процесса управления и учитывает только зависимость выходного процесса (выходной величины) y(t) САУ от входного процесса (входной величины) x(t) при утрате возможности физической интерпретации процессов управления, происходящих внутри САУ;
Слайд 7 Для описания математической модели САУ обычно используется три способа:
3) векторно-матричное описание САУ

в пространстве переменных состояния системы, позволяющее учитывать все параметры и переменные величины (координаты) САУ и вести расчёты с использованием ЭВМ при возможности физической интерпретации происходящих процессов управления в САУ.
Слайд 8Операторная функция передачи (ОФП) является важнейшим математическим описанием звена или САУ, представляющим

запись дифференциального уравнения в операторной форме в виде отношения изображений по Лапласу выходной y(t) и входной x(t) величин при нулевых начальных условиях, которая получается в виде:
Слайд 9Операторная функция передачи (ОФП)
Переводим дифференциальное уравнение в операторную форму, заменой:
и далее
и

далее
Слайд 10Операторная функция передачи (ОФП)
ОФП получается из дифференциального уравнения:
После перехода к операторной

форме:
Слайд 11Операторная функция передачи (ОФП)
Вынесем y(p) и x(p) за скобки:
Запишем ОФП:

Слайд 12ВРЕМЕННЫМИ ХАРАКТЕРИСТИКАМИ звена или САУ являются переходная функция h(t) и функция веса

w(t)
Переходной функцией (переходной характеристикой) h(t)=y(t) звена или САУ называется её реакция на единичное ступенчатое входное воздействие x(t)=1[t] при нулевых начальных условиях.
Функцией веса (весовой функцией, импульсной переходной характеристикой) w(t)=y(t) звена или САУ называется её реакция на единичное импульсное входное воздействие x(t)=δ(t) (дельта-функцию или функцию Дирака) при нулевых начальных условиях.
Слайд 13Дельта-функция или функция Дирака получается при дифференцировании единичной ступенчатой функции δ(t)=d1[t]/dt, при
![Дельта-функция или функция Дирака получается при дифференцировании единичной ступенчатой функции δ(t)=d1[t]/dt, при](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/365520/slide-12.jpg)
этом δ(t)=0 в любой момент времени t, кроме t=0, где величина импульса стремится к бесконечности при бесконечно малой продолжительности импульса, а площадь импульса равна единице ∫δ(t)dt=1.
Функция веса w(t) связана с переходной функцией h(t) операцией дифференцирования w(t)=dh(t)/dt.
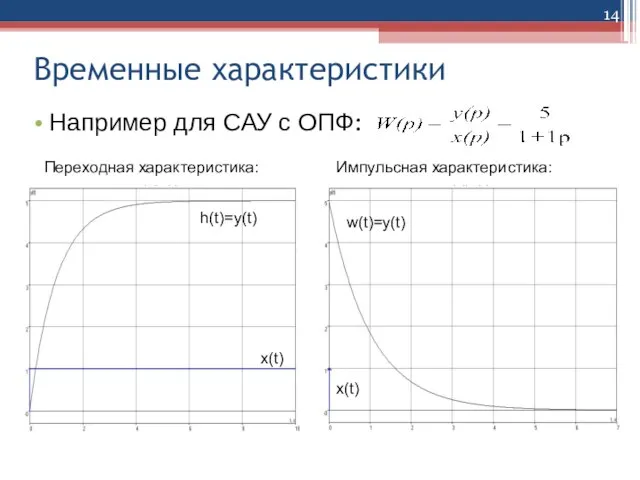
Слайд 14Временные характеристики
Например для САУ с ОПФ:
Переходная характеристика:
Импульсная характеристика:
x(t)
x(t)
h(t)=y(t)
w(t)=y(t)
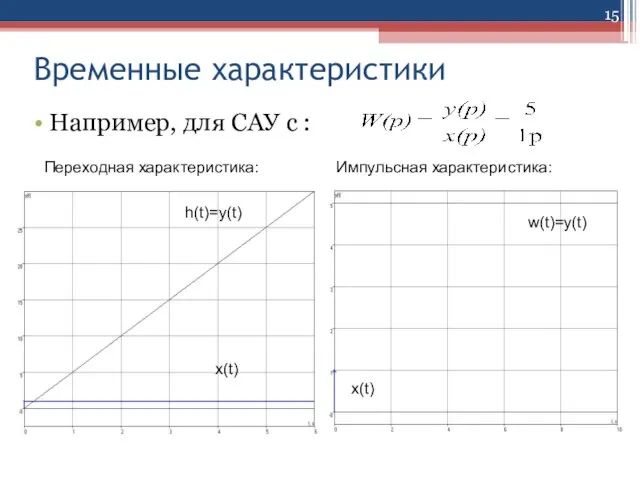
Слайд 15Временные характеристики
Например, для САУ с :
Переходная характеристика:
Импульсная характеристика:
x(t)
h(t)=y(t)
x(t)
w(t)=y(t)
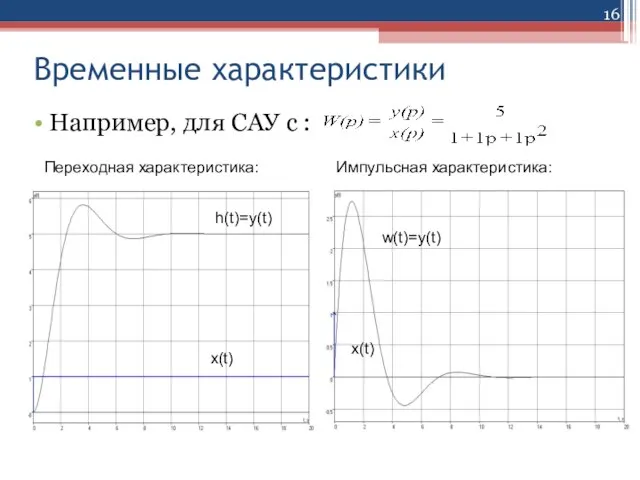
Слайд 16Временные характеристики
Например, для САУ с :
Переходная характеристика:
Импульсная характеристика:
x(t)
w(t)=y(t)
x(t)
h(t)=y(t)
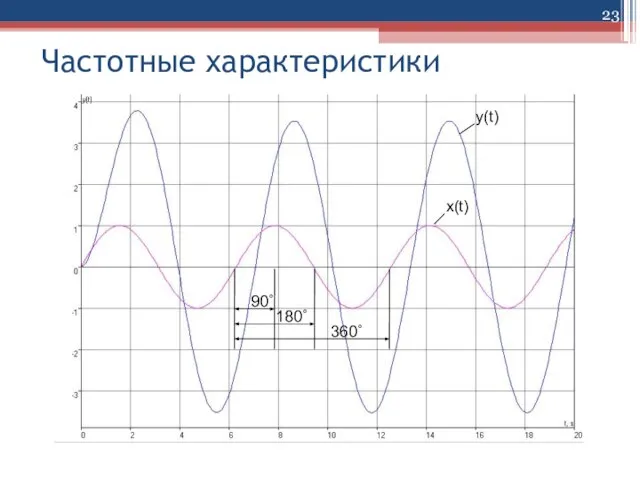
Слайд 17Частотные характеристики
Частотные характеристики представляют собой зависимость амплитуды и фазы выходного сигнала звена

или системы в установившемся режиме при гармоническом входном сигнале неизменной амплитуды и изменяемой частоты.
Частотные характеристики имеют важное значение для исследования систем автоматического управления, так как они характеризуют передаточные свойства звеньев и систем управления.
Слайд 18Частотные характеристики
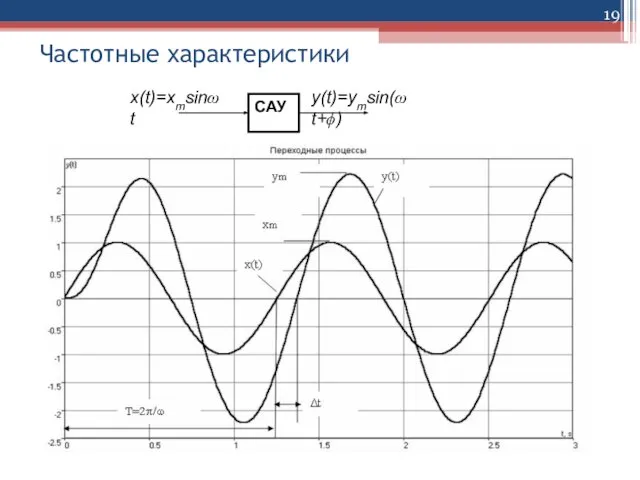
Если на вход САУ в момент времени t=0 приложено гармоническое

воздействие x (t) определенной частоты ω
x(t)=xmsinωt , то после окончания переходного процесса в системе установится режим установившихся вынужденных колебаний, а выходная величина y(t) будет изменяться по гармоническому закону с той же частотой ω, но с другой амплитудой ym и со сдвигом Δt во времени: y(t)=ym sin(ωt+ϕ), где ϕ = (Δt /T) ⋅360 – фазовый сдвиг между входным и выходным сигналами в градусах.
Слайд 20Частотные характеристики
Изменяя частоту входного сигнала ω от 0 до ∝ при

постоянном значении амплитуды xm, можно установить, что амплитуда и фазовый сдвиг выходного сигнала зависят от частоты входного сигнала.
Зависимости амплитуды ym и фазового сдвига ϕ от значений частоты ω характеризуют динамические свойства элементов и САУ.
Так как амплитуда выходного сигнала определяется также значением амплитуды входного сигнала, то возникает необходимость рассматривать отношение амплитуд ym /xm .
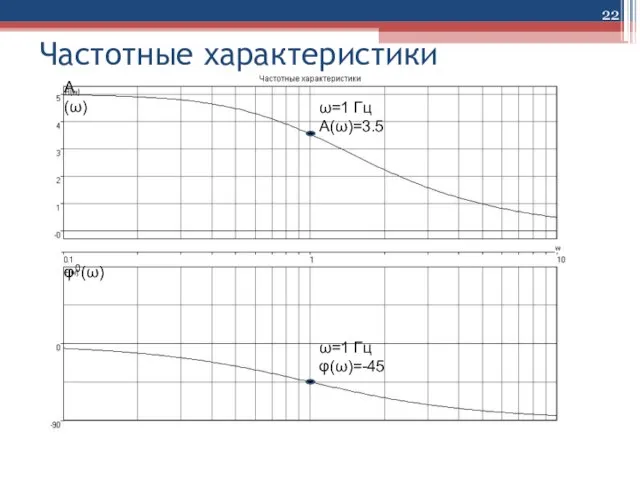
Слайд 21Частотные характеристики
Зависимость отношения амплитуд выходного и входного сигнала от частоты называют

амплитудной частотной характеристикой (АЧХ) и обозначают А(ω) .
АЧХ характеризует полосу пропускание элементом или САУ сигналов различной частоты. Пропускание оценивается по отношению амплитуд ym /xm.
Зависимость фазового сдвига между выходным и входным сигналами от частоты называют фазовой частотной характеристикой (ФЧХ) ϕ(ω).
Фазовый сдвиг <0 называется фазовым запаздыванием, фазовый сдвиг >0 называется фазовым опережением.
Слайд 23Частотные характеристики
y(t)
x(t)
360˚
180˚
90˚
Слайд 24Частотные характеристики
Амплитудно-фазовая характеристика (АФХ) (частотная передаточная функция, комплексный передачи) W(jω) звена

или САУ получается из операторной функции передачи (ОФП) W(p) этого звена или САУ при замене p = jω и изменении частоты ω от 0 до ∞.
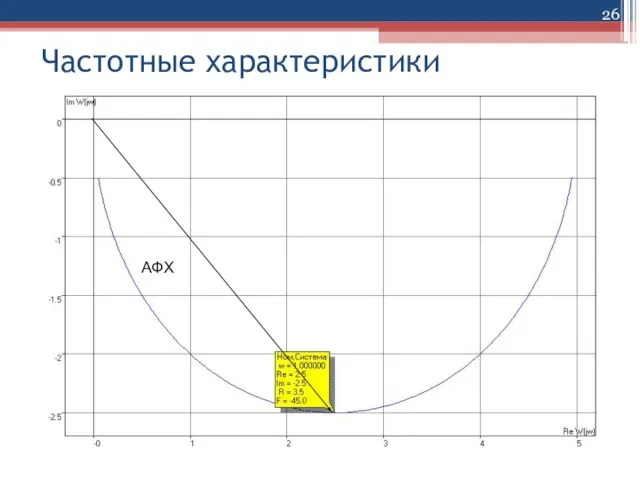
Слайд 25Частотные характеристики
Амплитудно-фазовая частотная характеристика W(jω)=U(ω)+jV(ω)=А(ω)е jφ(ω) является функцией комплексного переменного jω.
Каждому

значению частоты ωi соответствует комплексное число W(jωi), представленное на комплексной плоскости изображающим вектором длиной A(ωi ), расположенным к вещественной положительной оси под углом ϕ(ωi ).
Слайд 28Частотные характеристики
Выражение для амплитудно-фазовой характеристики конкретного элемента или САУ можно получить из

его передаточной функции подстановкой p=jω :
W(jω)=W(p) p=jω .
АФХ W(jω) может быть представлена:
в алгебраической форме
W(jω) = U(ω) + jV(ω);
в показательной форме
W(jω) = A(ω)e jϕ(ω) ;
в тригонометрической форме (по формуле Эйлера)
W(jω)=A(ω)cos[φ(ω)]+jA(ω)sin[φ(ω)],
где U(ω), V(ω) - вещественная и мнимая составляющие вектора W(jω);
A(⍵)= √ U2(ω)+V2(ω) – амплитудная частотная характеристика (АЧХ);
ϕ(ω)=arc tg [V(ω)/U(ω)]– фазовая частотная характеристика (ФЧХ).
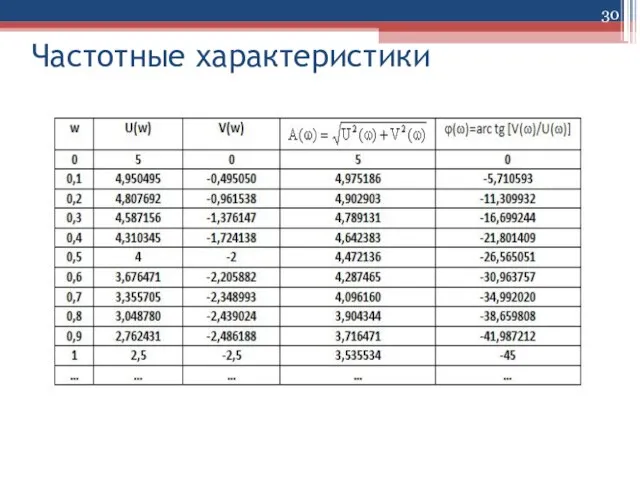
Слайд 29Частотные характеристики
Рассмотрим пример.
Пусть передаточная функция имеет вид:
При замене p = jω

получим АФХ в комплексной форме:
Получим вещественную и мнимую составляющие АФХ:
Слайд 33Частотные характеристики
В расчетах САУ широко используются логарифмические частотные характеристики.
Логарифмическая амплитудная частотная

характеристика (ЛАЧХ) звена или САУ строится в прямоугольной системе координат, где по оси ординат в линейном масштабе указывается величина ЛАЧХ в децибелах
L(ω)=20 lg⏐W(jω)⏐=20 lg A(ω),
а по оси абсцисс в логарифмическом масштабе указывается частота ω в 1/с (при этом равномерные изменения частоты в 10 раз представляются декадами).
Слайд 34Частотные характеристики
Децибел равен 1/10 бела.
Бел равен десятичному логарифму отношения мощностей на выходе

и входе звена или САУ, пропорциональному отношению квадратов напряжений, токов, скоростей или других величин (1бел = lgP2/P1 = lgU22/U12).
Поэтому множитель 20=2∙10, где 2 отражает логарифмирование квадрата отношения выходной и входной величин, а 10 – перевод белов в децибелы.
Слайд 35Частотные характеристики
Логарифмическая фазовая частотная характеристика (ЛФЧХ) φ(ω)=arctg[V(ω)/U(ω)] звена или САУ строится по
![Частотные характеристики Логарифмическая фазовая частотная характеристика (ЛФЧХ) φ(ω)=arctg[V(ω)/U(ω)] звена или САУ строится](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/365520/slide-34.jpg)
оси ординат
в линейном масштабе, где указывается угол фазового сдвига ϕ(ω) в радианах или угловых градусах, а по оси абсцисс указывается частота ω в логарифмическом масштабе в 1/с.
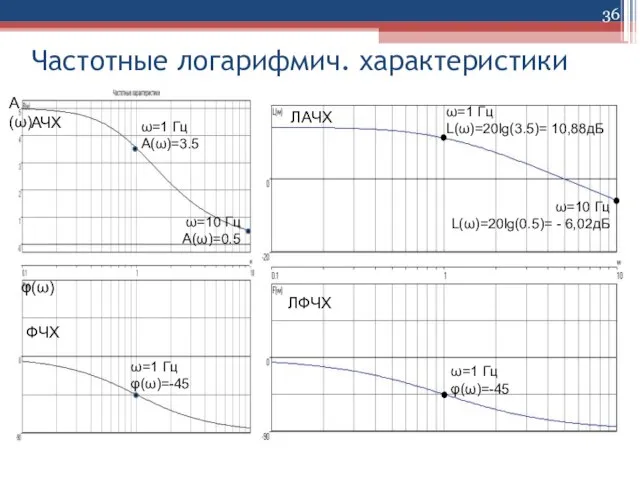
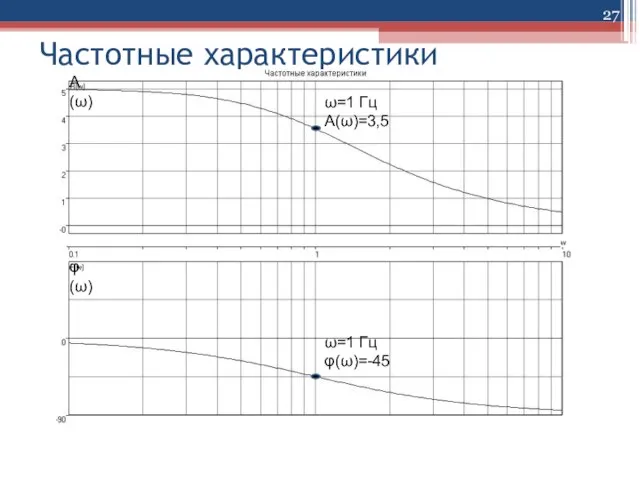
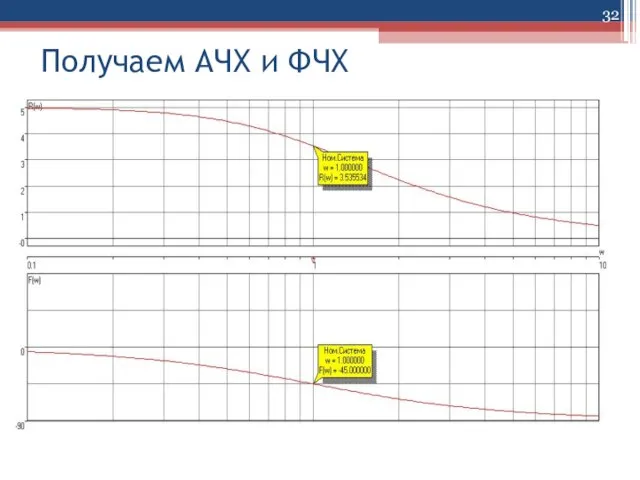
Слайд 36Частотные логарифмич. характеристики
ω=1 Гц
L(ω)=20lg(3.5)= 10,88дБ
Слайд 381.2. Типовые звенья САУ и их характеристики
Звенья с математическим описанием обыкновенными

дифференциальными уравнениями первого и второго порядка называются типовыми динамическими звеньями.
Из типовых динамических звеньев составляются алгоритмические структурные схемы САУ.
Знание характеристик типовых звеньев облегчает изучение свойств САУ.
Слайд 391.2. Типовые звенья САУ и их характеристики
Классификацию типовых звеньев удобно осуществить, рассматривая

различные частные случаи общего дифференциального уравнения:
В операторной форме:
Слайд 401.2. Типовые звенья САУ и их характеристики
Вынесем x(p) и y(p) за скобки:
Передаточная

функция в общем виде для типовых звеньев САУ:
Слайд 411.2. Типовые звенья САУ и их характеристики
Принято уравнение:
записывать в виде (разделив на

):
где
Параметры T2, T1, τ называются постоянными времени, измеряемыми в секундах;
K называется коэффициентом передачи.
Слайд 421.2. Типовые звенья САУ и их характеристики
Передаточная функция из уравнения:
в общем виде

для типовых звеньев САУ:
Слайд 43Типовые динамические звенья делятся по зависимостям выходной величины y от входного воздействия

x в установившихся режимах работы на 4 типа:
1) позиционные, в которых выходная величина пропорциональна входному воздействию y=Kx;
2) интегрирующие, в которых выходная величина пропорциональна интегралу от входной величины y=K∫xdt;
3) дифференцирующие, в которых выходная величина пропорциональна дифференциалу (первой производной по времени) от входного воздействия y=K dx/dt;
4) запаздывающие, в которых выходная величина равна входной величине, сдвинутой в текущем времени на время запаздывания τ y=x(t – τ).
Слайд 441.2. Типовые звенья САУ и их характеристики
Пример:

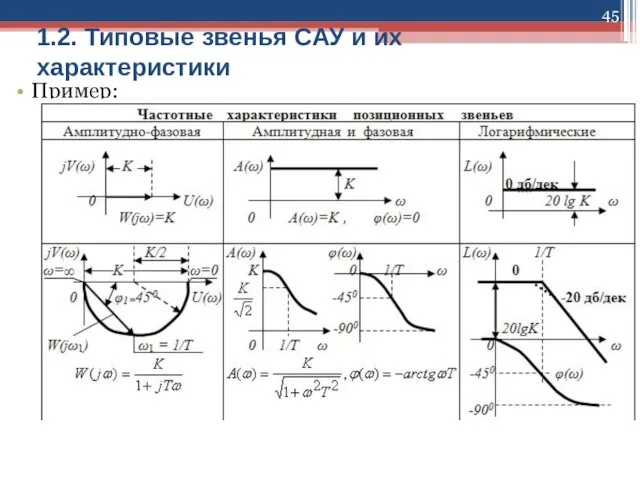
Слайд 451.2. Типовые звенья САУ и их характеристики
Пример:
Слайд 461.2. Типовые звенья САУ и их характеристики
Рассмотрим методику получения временных и частотных

характеристик на примере позиционного апериодического (инерционного) звена первого порядка имеющего передаточную функцию:
где T – постоянная времени звена; K – коэффициент передачи звена.
Дифференциальное уравнение процесса управления:
Слайд 471.2. Типовые звенья САУ и их характеристики
Переходная функция звена h(t)=y(t) получается

в виде суммы общего и частного решений дифференциального уравнения при нулевых начальных условиях и подаче на вход единичного ступенчатого воздействия x(t)=1[t]:
где p= –1/T – корень характеристического уравнения Тр+1=0; С=–K∙1[t] – постоянная интегрирования при нулевых начальных условиях y(t)t=0=Ce–0/T+K∙1[t]=0.
Слайд 481.2. Типовые звенья САУ и их характеристики
Весовая функция звена определяется
дифференцированием h(t)

по времени:
Слайд 491.2. Типовые звенья САУ и их характеристики
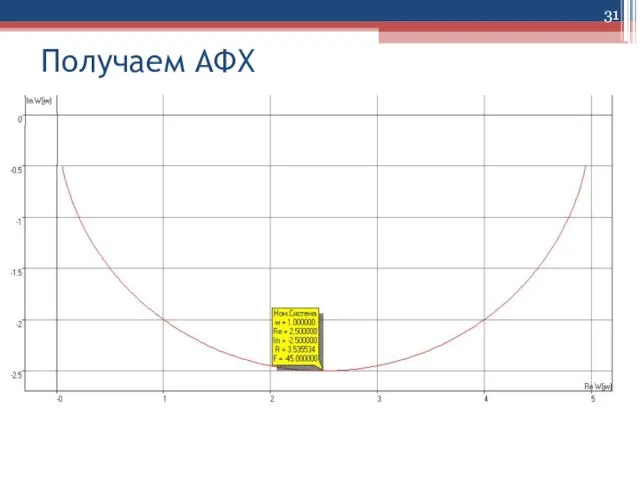
Частотная амплитудно-фазовая характеристика (АФХ) получается из

уравнения ОПФ:
при p=j⍵ АФХ опишется уравнением:
при изменении ω от 0 до бесконечности АФХ имеет вид полуокружности с радиусом K/2.
Слайд 501.2. Типовые звенья САУ и их характеристики
Амплитудная А(ω) и фазовая φ(ω) частотные

характеристики (АЧХ и ФЧХ) определяются из:
и имеют вид:
при ω=0 A(ω)=K, при ω=1/T A(ω)= , при ω=∞ A(ω)= 0.
фазовый сдвиг при изменении частоты от 0 до ∞
изменяется от 00 до –900 и ϕ(ω)= – 450 при ω=1/T.
Слайд 511.2. Типовые звенья САУ и их характеристики
Амплитудная А(ω) и фазовая φ(ω) частотные
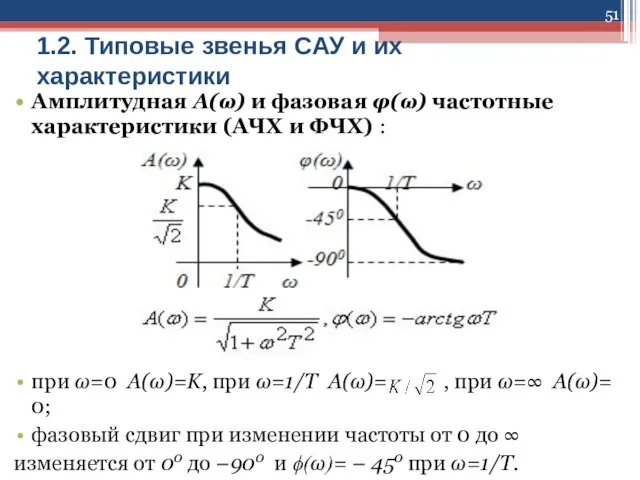
характеристики (АЧХ и ФЧХ) :
при ω=0 A(ω)=K, при ω=1/T A(ω)= , при ω=∞ A(ω)= 0;
фазовый сдвиг при изменении частоты от 0 до ∞
изменяется от 00 до –900 и ϕ(ω)= – 450 при ω=1/T.
Слайд 521.2. Типовые звенья САУ и их характеристики
Логарифмическая амплитудная частотная характеристика (ЛАЧХ) описывается

выражением:
ЛАЧХ, построенная по данному уравнению имеет две асимптоты:
а) при частотах ω<1/T в ω2Т2<<1, тогда ω2T2+1≈1 и асимптота ЛАЧХ представляется горизонтальной прямой;
б) при частотах ω >1/T в ω2Т2>>1, тогда и асимптота ЛАЧХ L(ω)Б=20lgK–20lgωT представляется прямой линией с наклоном минус 20 децибел на декаду (дб/дек) относительно оси абсцисс.
Слайд 531.2. Типовые звенья САУ и их характеристики
Эти асимптоты сопрягаются при частоте сопряжения

ωС=1/T, при этой частоте асимптотическая ЛАЧХ имеет превышение коэффициента передачи по сравнению с непрерывной ЛАЧХ на величину:
которой в расчётах, ввиду малости, можно пренебречь и считать, что асимптотическая ЛАЧХ состоит из горизонтальной и наклонной прямых, образованных отрезками асимптот А и Б, сопрягающихся при ωС=1/T.
Слайд 541.2. Типовые звенья САУ и их характеристики
Логарифмическая фазовая частотная характеристика (ЛФЧХ) звена
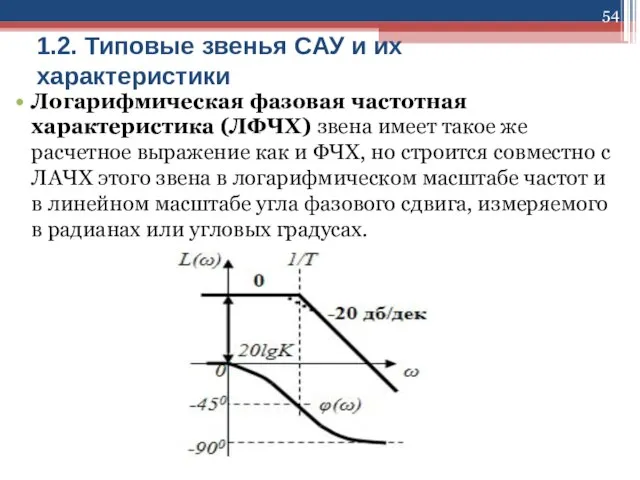
имеет такое же расчетное выражение как и ФЧХ, но строится совместно с ЛАЧХ этого звена в логарифмическом масштабе частот и в линейном масштабе угла фазового сдвига, измеряемого в радианах или угловых градусах.
Слайд 551.2. Типовые звенья САУ и их характеристики
Аналогичным путем получаются временные и частотные

характеристики других типовых звеньев САУ, математические модели которых представлены линейными дифференциальными уравнениями не выше второго порядка.
Линеаризация дифференциальных уравнений обычно осуществляется способом их разложения в степенной ряд Тейлора с отбрасыванием членов выше второго порядка.
Слайд 571.3. Преобразование структурных схем САУ
Изображение САУ в виде совокупности однонаправленных типовых звеньев

с указанием связей между ними и с внешней средой называется структурной схемой САУ (алгоритмической структурной схемой или просто структурой САУ), которая является графической интерпретацией описания математической модели САУ операторными функциями передачи (ОФП).
Данный способ составляет сущность структурного метода представления САУ различной физической природы, который дает наглядное представление взаимосвязи элементов, звеньев и частей САУ и позволяет оценивать основные свойства переходных и установившихся процессов в САУ.
Слайд 581.3. Преобразование структурных схем САУ
На структурных схемах САУ каждое звено обозначается прямоугольником,

в котором записывается ОФП звена или её обозначение.
Входные воздействия обозначаются стрелками, направленными в звено, выходные величины – стрелками, направленными из звена.
Сумматоры обозначаются кружком, в который направлены стрелки суммируемых величин (вычитаемые величины обозначаются с минусом около стрелки), а результирующая величина обозначается стрелкой, выходящей из кружка.
Устройства САУ, в которых имеется обратная связь, представляется в структурной схеме контуром с обратной связью.
Слайд 591.3. Преобразование структурных схем САУ
производится с целью получения упрощенного эквивалентного
звена или
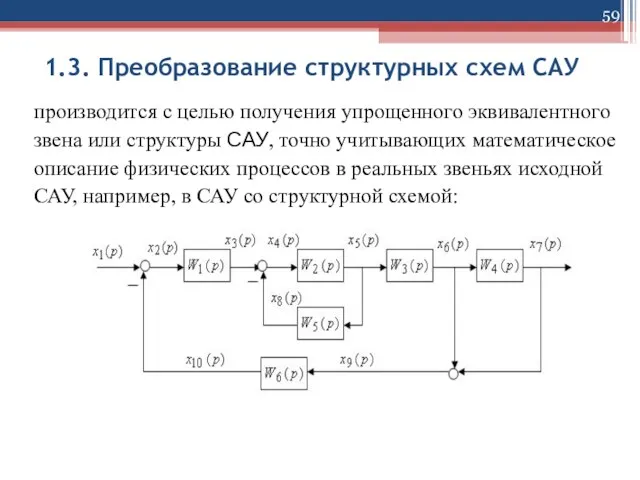
структуры САУ, точно учитывающих математическое
описание физических процессов в реальных звеньях исходной
САУ, например, в САУ со структурной схемой:
Слайд 601.3. Преобразование структурных схем САУ
Для этого используются следующие шесть основных правил эквивалентных

преобразований структурных схем без изменений ОФП САУ:
1. Преобразование последовательно соединенных звеньев:
Слайд 611.3. Преобразование структурных схем САУ
Используются следующие шесть основных правил эквивалентных преобразований структурных
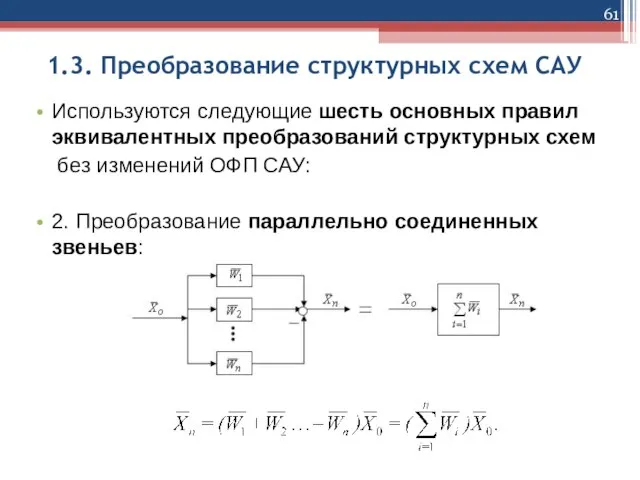
схем
без изменений ОФП САУ:
2. Преобразование параллельно соединенных звеньев:
Слайд 621.3. Преобразование структурных схем САУ
Используются следующие шесть основных правил эквивалентных преобразований структурных

схем
без изменений ОФП САУ:
3. Правило преобразования контура с обратной связью:
+ для отрицательной обратной связи;
- для положительной обратной связи.
Слайд 631.3. Преобразование структурных схем САУ
Используются следующие шесть основных правил эквивалентных преобразований структурных

схем
без изменений ОФП САУ:
4. Правила переноса узла разветвления сигнала:
а) по направлению распространения сигнала
Слайд 641.3. Преобразование структурных схем САУ
Используются следующие шесть основных правил эквивалентных преобразований структурных
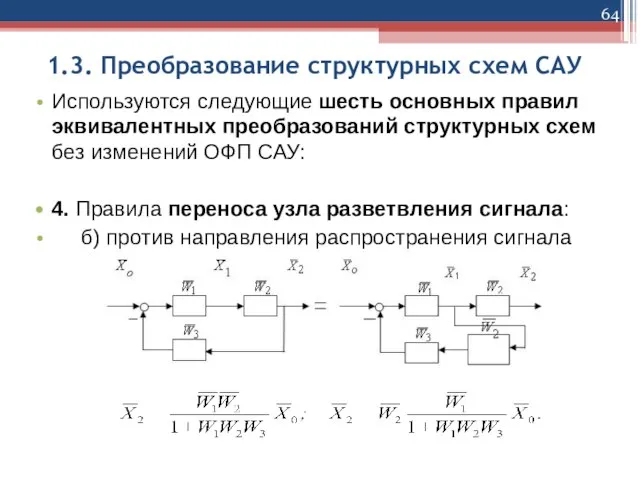
схем без изменений ОФП САУ:
4. Правила переноса узла разветвления сигнала:
б) против направления распространения сигнала
Слайд 651.3. Преобразование структурных схем САУ
Используются следующие шесть основных правил эквивалентных преобразований структурных

схем
без изменений ОФП САУ:
5. Правила переноса сумматора сигналов:
а) по направлению распространения сигнала
Слайд 661.3. Преобразование структурных схем САУ
Используются следующие шесть основных правил эквивалентных преобразований структурных

схем
без изменений ОФП САУ:
5. Правила переноса сумматора сигналов:
б) против направления распространения сигнала
Слайд 671.3. Преобразование структурных схем САУ
Используются следующие шесть основных правил эквивалентных преобразований структурных

схем
без изменений ОФП САУ:
6. Правила перестановка сумматоров в структурных схемах с перекрещивающимися обратными связями
для выделения явно выраженных замкнутых контуров управления.
Перестановка сумматоров выполняется в два этапа.
Слайд 681.3. Преобразование структурных схем САУ
В структурных схемах с перекрещивающимися обратными связями:
а) на
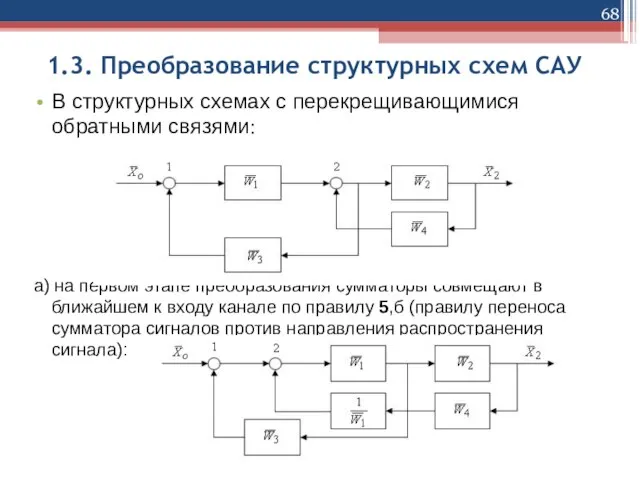
первом этапе преобразования сумматоры совмещают в ближайшем к входу канале по правилу 5,б (правилу переноса сумматора сигналов против направления распространения сигнала):
Слайд 691.3. Преобразование структурных схем САУ
б) на втором этапе преобразования сумматоры переставляют местами
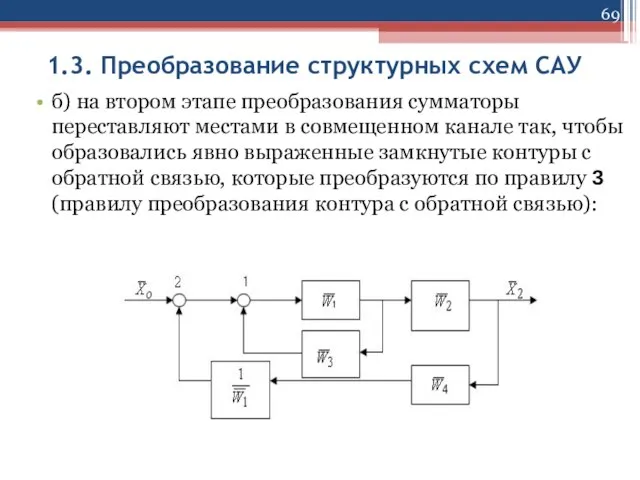
в совмещенном канале так, чтобы образовались явно выраженные замкнутые контуры с обратной связью, которые преобразуются по правилу 3 (правилу преобразования контура с обратной связью):
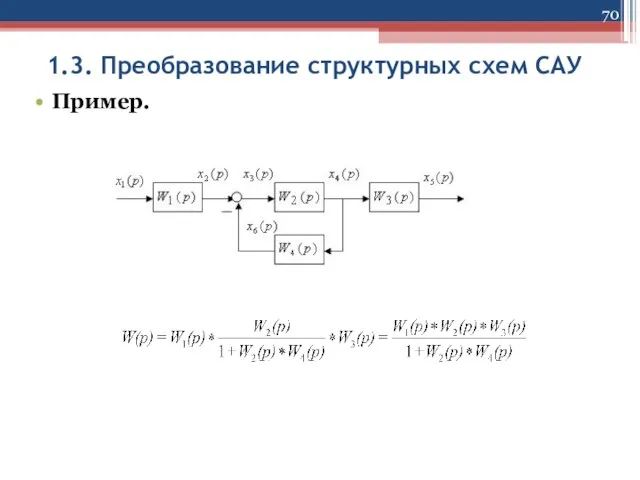
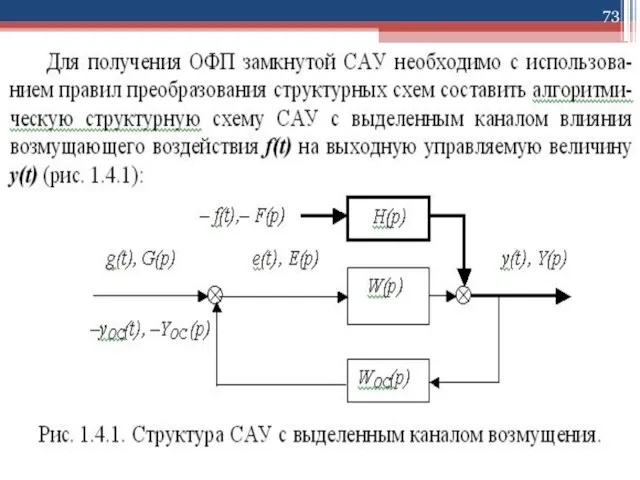
Слайд 701.3. Преобразование структурных схем САУ
Пример.











![Дельта-функция или функция Дирака получается при дифференцировании единичной ступенчатой функции δ(t)=d1[t]/dt, при](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/365520/slide-12.jpg)














![Частотные характеристики Логарифмическая фазовая частотная характеристика (ЛФЧХ) φ(ω)=arctg[V(ω)/U(ω)] звена или САУ строится](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/365520/slide-34.jpg)






































 Материалы для автоворонки
Материалы для автоворонки Презентация на тему Плоские черви
Презентация на тему Плоские черви  Фотоискусство
Фотоискусство lektsia_6
lektsia_6 Методы развития внимания у детей дошкольного возраста
Методы развития внимания у детей дошкольного возраста  Буддизм
Буддизм Аэрозоль
Аэрозоль Энергосбережение при грануляции металлургического шлака
Энергосбережение при грануляции металлургического шлака История династии Романовых
История династии Романовых Аксиологические основы профессиональной подготовки студентов международного профиля
Аксиологические основы профессиональной подготовки студентов международного профиля Подарок юной рукодельнице
Подарок юной рукодельнице Белорусский костюм (1)
Белорусский костюм (1) Врачебный диагноз
Врачебный диагноз Wide Range of UPVC Windows & Doors
Wide Range of UPVC Windows & Doors Агляд-конкурс мастацкай самадзейнай творчасці сярод груп першага курса Я - беларус. Я - зерне, код народа
Агляд-конкурс мастацкай самадзейнай творчасці сярод груп першага курса Я - беларус. Я - зерне, код народа Информационное сообщениеВ.Н. Федулин
Информационное сообщениеВ.Н. Федулин Front Page
Front Page МАДОУ детский сад «Надежда» г.Кирово-Чепецк Кировская область Коррекционно-педагогическая работа с использованием ло
МАДОУ детский сад «Надежда» г.Кирово-Чепецк Кировская область Коррекционно-педагогическая работа с использованием ло «5 факторов эффективного поискового продвижения
«5 факторов эффективного поискового продвижения маркетинговые коммуникации
маркетинговые коммуникации  Олимпиады школьников по направлению «Информационная безопасность»
Олимпиады школьников по направлению «Информационная безопасность» От Сиднея вдоль Большого Водораздельного хребта
От Сиднея вдоль Большого Водораздельного хребта Презентация на тему Водоросли
Презентация на тему Водоросли  7 февраля 2006 г. Пресс-конференция «Вырваться из Сумрака!»
7 февраля 2006 г. Пресс-конференция «Вырваться из Сумрака!» Кластерный анализ. Метод к – средних
Кластерный анализ. Метод к – средних СЕМЕЙНЫЙ КЛУБ «МАМИНЫ ГЛАЗА»
СЕМЕЙНЫЙ КЛУБ «МАМИНЫ ГЛАЗА» Обзор зарплат по должностям дилерских авто центров
Обзор зарплат по должностям дилерских авто центров Преступление. Разновидности преступлений
Преступление. Разновидности преступлений