Содержание
- 2. Алгебра высказываний Алгебра высказываний была разработана для того, чтобы определять истинность или ложность составных высказываний, не
- 3. Логические переменные Логические переменные – простые высказывания, содержащие только одну мысль. Обозначаются буквами латинского алфавита: A,
- 4. Логические переменные Например, два простых высказывания: А = «2 × 2 = 4» истина (1) В
- 5. В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: «ИСТИНА» (1)
- 6. В алгебре высказываний над логическими переменными (над высказываниями) можно производить определенные логические операции, в результате которых
- 7. Составные высказывания Высказывания, состоящие из нескольких простых суждений и содержащие в себе более, чем одну простую
- 8. Логические операции Конъюнкция (логическое умножение, «И») Дизъюнкция (логическое сложение, «ИЛИ») Инверсия (логическое отрицание, «НЕ») Импликация (логическое
- 9. Объединение двух или нескольких высказываний в одно с помощью союза «И» называется операцией логического умножения, или
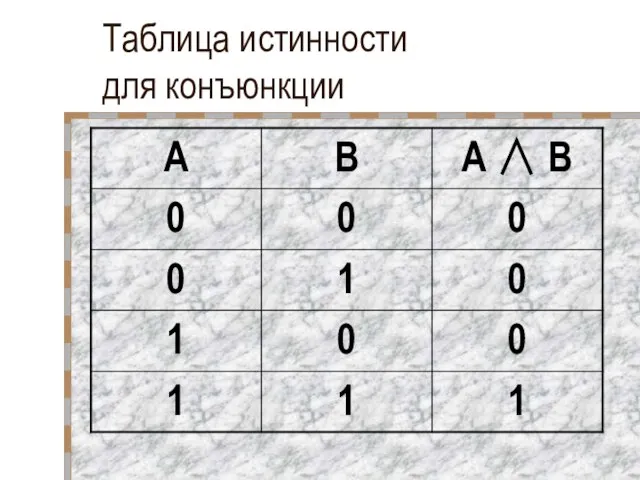
- 10. Логическая функция, полученная в результате конъюнкции, истинна тогда и только тогда, когда истинны все входящие в
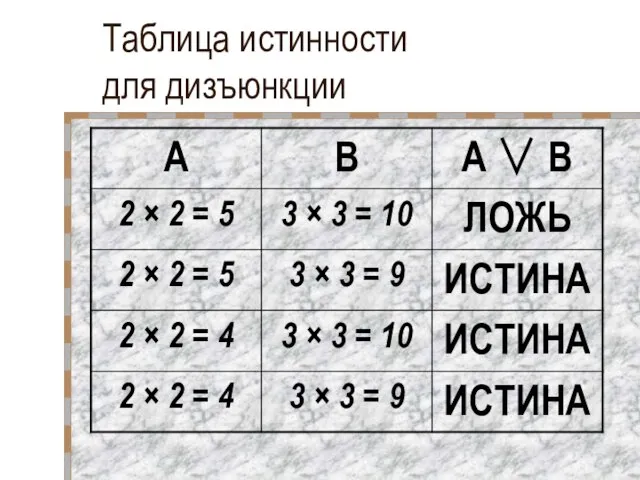
- 11. Конъюнкция. Определите истинность логической функции «2 × 2 = 5» И «3 × 3 = 10»
- 12. Запись конъюнкции на формальном языке алгебры высказываний F(A,B) = A & B или F(A,B) = A
- 13. Значение логической функции определяется по ее таблице истинности Таблица истинности показывает какие значения принимает логическая функция
- 14. Таблица истинности для конъюнкции
- 15. Таблица истинности для конъюнкции
- 16. Объединение двух или нескольких высказываний в одно с помощью союза «ИЛИ» называется операцией логического сложения, или
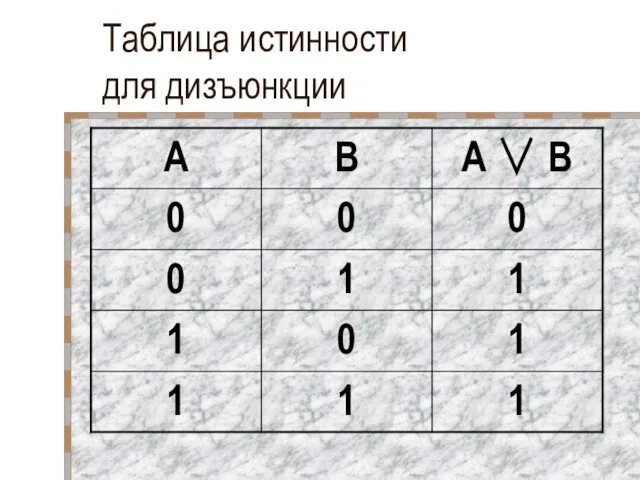
- 17. Логическая функция, полученная в результате дизъюнкции, истинна тогда, когда истинна хотя бы одна из входящих в
- 18. Дизъюнкция. Определите истинность логической функции «2 × 2 = 5» ИЛИ «3 × 3 = 10»
- 19. Запись дизъюнкции на формальном языке алгебры высказываний F(A,B) = A ∨ B Также может встретиться запись,
- 20. Таблица истинности для дизъюнкции
- 21. Таблица истинности для дизъюнкции
- 22. Присоединение частицы «НЕ» к высказыванию называется операцией логического отрицания, или инверсией
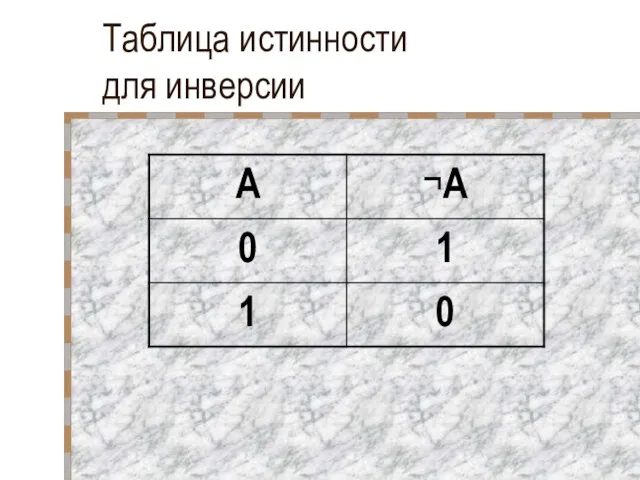
- 23. Логическое отрицание (инверсия) делает истинное высказывание ложным, а ложное – истинным [логическая отрицательная единица, перевертыш]
- 24. Инверсия Пусть A = «2 × 2 = 4» – истинное высказывание, тогда F(A) = «2
- 25. Запись инверсии на формальном языке алгебры высказываний F(A) = ¬A или F(A) = Ā Также может
- 26. Таблица истинности для инверсии
- 27. Таблицы истинности основных логических функций Логическое умножение A 0 0 1 1 B 0 1 0
- 28. Дополнительные логические функции Импликацию и эквивалентность можно выразить через конъюнкцию, дизъюнкцию и отрицание, поэтому их называют
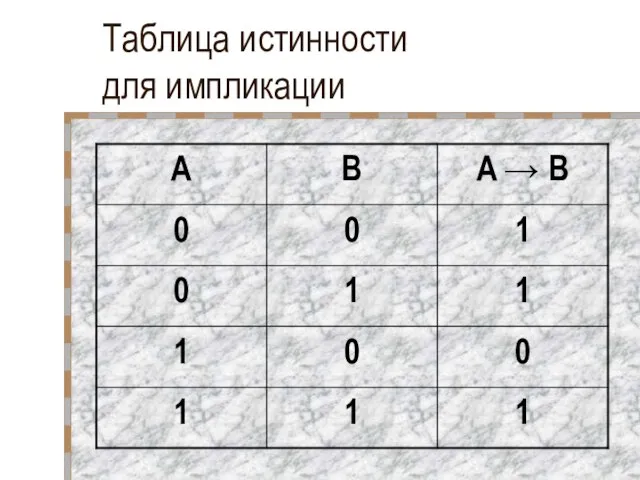
- 29. Импликация Объединение двух высказываний, из которых первое является условием, а второе – следствием из него, называется
- 30. Импликация Импликация ложна тогда и только тогда, когда условие истинно, а следствие ложно Пример: Если выучишь
- 31. Таблица истинности для импликации
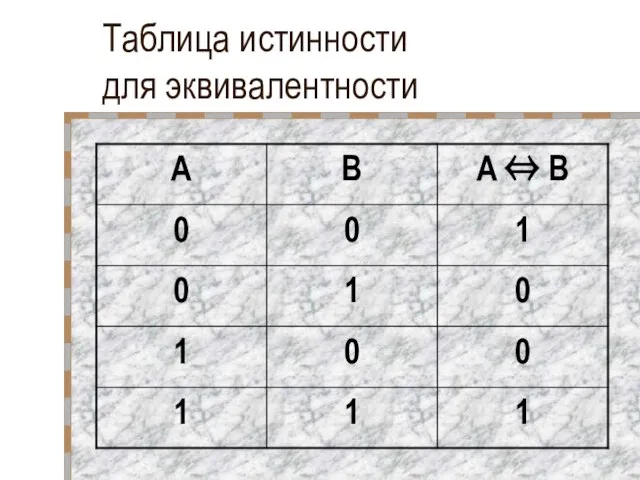
- 32. Эквивалентность Эквивалентность – это логическая операция, объединяющая два простых высказывания в одно составное и которое является
- 33. Таблица истинности для эквивалентности
- 34. Переместительный Дизъюнкция: X ∨ Y ≡ Y ∨ X Конъюнкция: X ∧ Y ≡ Y ∧
- 35. Сочетательный Дизъюнкция: X ∨ (Y ∨ Z) ≡ (X ∨ Y) ∨ Z Конъюнкция: X ∧
- 36. Распределительный Дизъюнкция: X ∧ (Y ∨ Z) ≡ X ∧ Y ∨ X ∧ Z Конъюнкция:
- 37. Правила де Моргана Дизъюнкция: ¬(X ∨ Y) ≡ ¬X ∧ ¬Y Конъюнкция: ¬(X ∧ Y) ≡
- 38. Идемпотенции Дизъюнкция: X ∨ X ≡ X Конъюнкция: X ∧ X ≡ X Основные законы алгебры
- 39. Поглощения Дизъюнкция: X ∨ (X ∧ Y) ≡ X Конъюнкция: X ∧ (X ∨ Y) ≡
- 40. Склеивания Дизъюнкция: (X ∧ Y) ∨ (¬X ∧ Y) ≡ Y Конъюнкция: (X ∨ Y) ∧
- 41. Переменная со своей инверсией Дизъюнкция: X ∨ ¬X ≡ 1 Конъюнкция: X ∧ ¬X ≡ 0
- 42. Операция с константами Дизъюнкция: X ∨ 0 ≡ X, X ∨ 1 ≡ 1 Конъюнкция: X
- 43. Двойного отрицания ¬(¬X) ≡ X Основные законы алгебры высказываний
- 45. Скачать презентацию


















![Логическое отрицание (инверсия) делает истинное высказывание ложным, а ложное – истинным [логическая отрицательная единица, перевертыш]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/326785/slide-22.jpg)

















 Царевна лягушка
Царевна лягушка человека
человека Основы маркетинга
Основы маркетинга Іван Паламарчук ItEvent`09. - презентация
Іван Паламарчук ItEvent`09. - презентация Федеральное казначейство. Ротация гражданских служащих. Нормативно-правовая база
Федеральное казначейство. Ротация гражданских служащих. Нормативно-правовая база Ребенок мало самостоятельности мало ответственности
Ребенок мало самостоятельности мало ответственности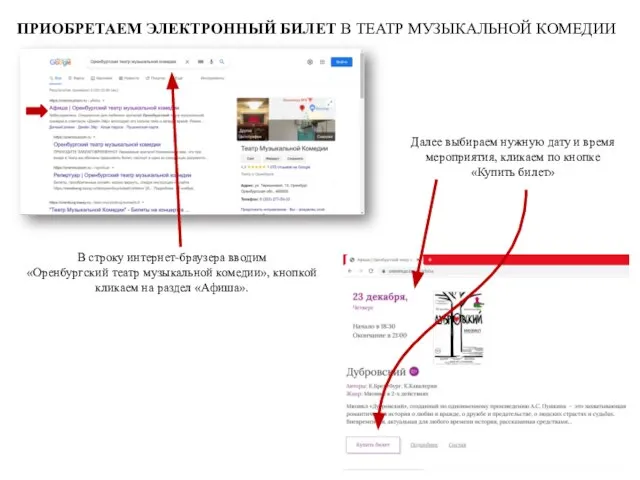 Приобретаем электронный билет в театр музыкальной комедии
Приобретаем электронный билет в театр музыкальной комедии Ecostandard Group
Ecostandard Group Презентация на тему Золотая осень
Презентация на тему Золотая осень  Проведение тактического ориентирования на макете местности
Проведение тактического ориентирования на макете местности Преступления против конституционных прав и свобод человека и гражданина
Преступления против конституционных прав и свобод человека и гражданина Christopher Marlowe
Christopher Marlowe Что такое компьютерные сети?
Что такое компьютерные сети? Жабы
Жабы Рождество в Китае
Рождество в Китае ООО «ЭКСИМ-ПРИБОР»
ООО «ЭКСИМ-ПРИБОР» Презентация на тему Биологические ритмы человека
Презентация на тему Биологические ритмы человека  Примеры речевых форм эмоциональной экспрессии
Примеры речевых форм эмоциональной экспрессии Презентация на тему Кто придумал первую ракету?
Презентация на тему Кто придумал первую ракету? Государственный бюджет
Государственный бюджет Маркеры для оптических измерительных систем. Паспорт
Маркеры для оптических измерительных систем. Паспорт 10 класс Международные организации
10 класс Международные организации Сборная презентация к курсу лекций по история России XVII—XVIII вв. Автор: проф. Н.В.Козлова
Сборная презентация к курсу лекций по история России XVII—XVIII вв. Автор: проф. Н.В.Козлова Аудит учредительных документов и формирования уставного капитала
Аудит учредительных документов и формирования уставного капитала КОМЕТА 2
КОМЕТА 2 Изостудия Этюд. Птичка. Графика
Изостудия Этюд. Птичка. Графика КОРРУПЦИЯ:ОТКУДА ЧТО БЕРЕТСЯ?
КОРРУПЦИЯ:ОТКУДА ЧТО БЕРЕТСЯ? Дом моей мечты
Дом моей мечты