Основы ТАУ. Передаточная функция цепи звеньев. Структурные преобразования. Лекция 9

Литература

Введение
Системы автоматического управления (САУ) как правило, являются замкнутыми системами, но при проектировании и анализе качества процесса управления часто возникает необходимость рассмотрения разомкнутой цепи звеньев, которая затем замыкается. Предварительно рассмотрим различные способы соединения динамических звеньев между собой.

Цепь из последовательно соединенных звеньев
Структурная схема последовательного соединения представлена на рис
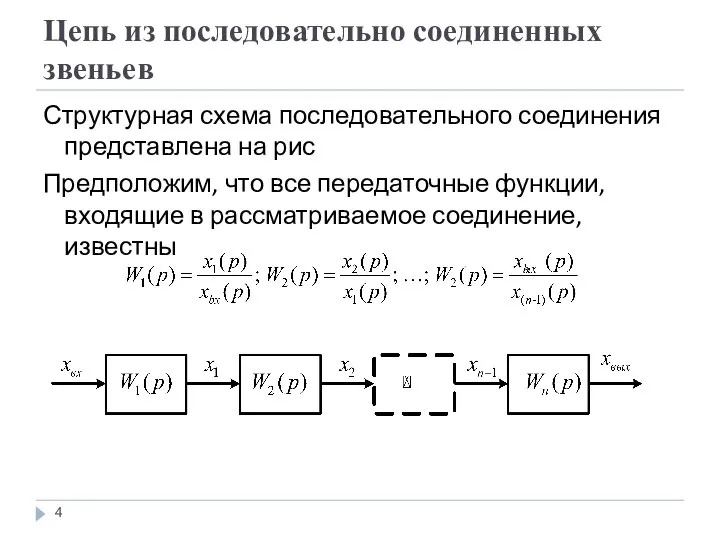
Предположим, что все передаточные функции, входящие в рассматриваемое соединение, известны

Цепь из последовательно соединенных звеньев
Если перемножить между собой все левые части передаточных функций и все правые части, то получится передаточная функция последовательной цепи звеньев
Передаточная функция разомкнутой цепи последовательно соединенных звеньев равна произведению передаточных функций всех звеньев.

Цепь из параллельно соединенных звеньев
Структурная схема параллельного соединения представлена на рис.
Если известны все передаточные функции звеньев ,
то выходной сигнал цепи
передаточная функция параллельно соединенных звеньев имеет вид

Цепь из параллельно соединенных звеньев
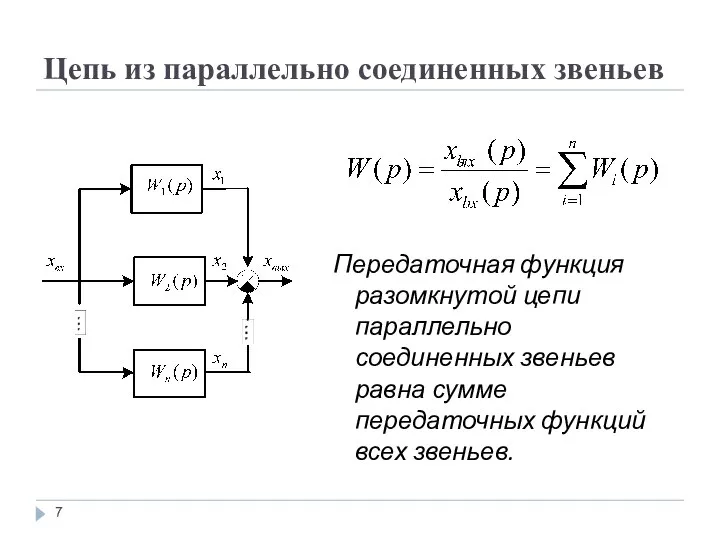
Передаточная функция разомкнутой цепи параллельно соединенных звеньев равна сумме передаточных функций всех звеньев.

Цепи с местной обратной связью
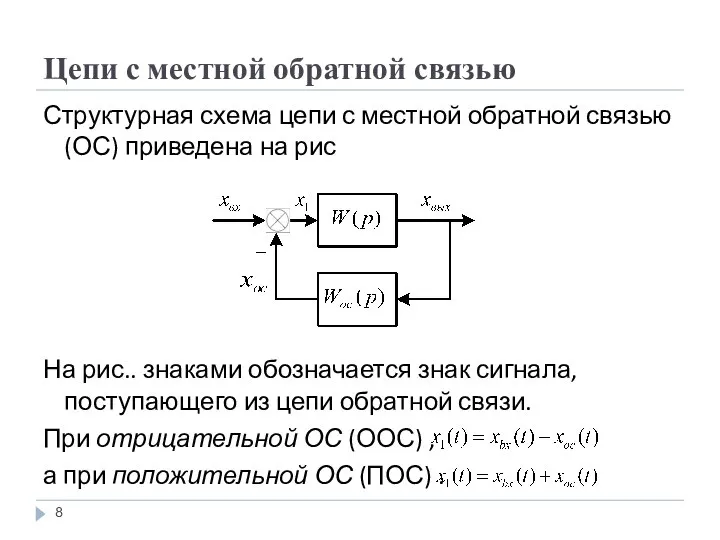
Структурная схема цепи с местной обратной связью (ОС) приведена на рис
На рис.. знаками обозначается знак сигнала, поступающего из цепи обратной связи.
При отрицательной ОС (ООС) ,
а при положительной ОС (ПОС) .

Цепи с местной обратной связью
Составим систему уравнений, описывающую динамическое поведение звена с ОС
Следовательно, передаточная функция цепи с ОС будет иметь вид

Цепи с местной обратной связью
Передаточная функция цепи с местной ОС равна отношению передаточной функции прямой цепи
к выражению ,
причем, знак «+» соответствует цепи с ООС,
а знак «–» сответствует ПОС.

Общий коэффициент усиления разомкнутой цепи
Статический режим работы характеризуется коэффициентом усиления. Чтобы определить коэффициент усиления необходимо в передаточной функции цепи положить
Общий коэффициент усиления последовательного соединения равен произведению коэффициентов усиления всех последовательно соединенных звеньев
где – коэффициент усиления отдельного звена.

Общий коэффициент усиления разомкнутой цепи
Коэффициент усиления параллельного соединения равен сумме коэффициентов всех параллельно соединенных звеньев
Коэффициент усиления цепи с местной ОС равен отношению коэффициента усиления k прямой цепи к выражению

Структурные преобразования
Для удобства расчетов автоматических систем бывает необходимо преобразовывать структурную схему системы к какому-либо желаемому виду.
Например, для построения ЛАЧХ удобно, чтобы разомкнутая часть САУ состояла из цепи последовательно соединенных звеньев.
Рассмотрим некоторые правила простейшего преобразования структурных схем, пользуясь которыми можно производить эквивалентные преобразования структурных схем к желаемому виду

Структурные преобразования
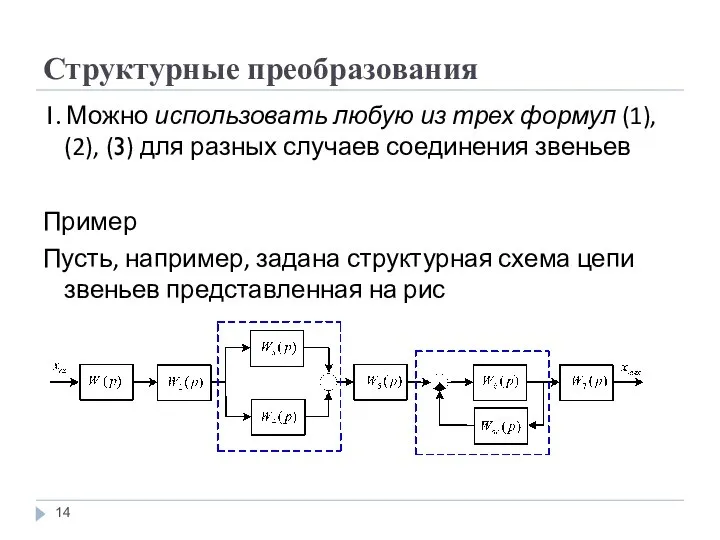
1. Можно использовать любую из трех формул (1), (2), (3) для разных случаев соединения звеньев
Пример
Пусть, например, задана структурная схема цепи звеньев представленная на рис

Структурные преобразования
Используя формулы (1), (2), (3) её можно преобразовать к цепи последовательных звеньев. Такая структурная схема представлена на рис.

Структурные преобразования
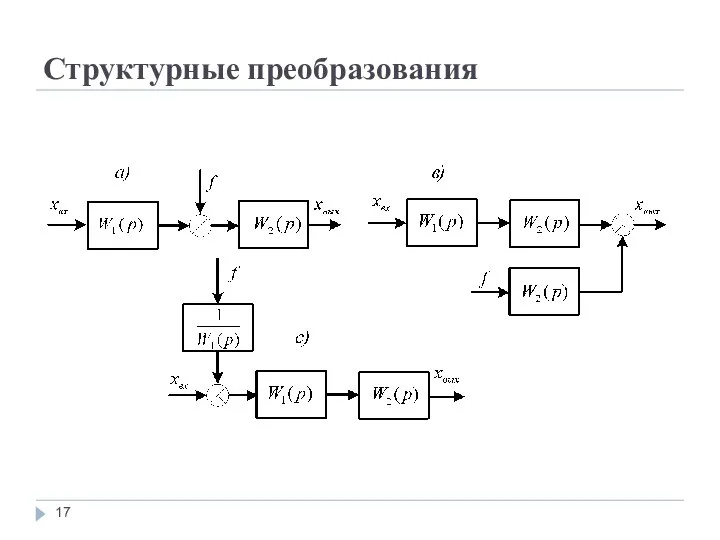
2. Можно переносить внешнее воздействие вперед или назад по цепи таким образом, чтобы не менялась передача сигнала на выход этой цепи.
Например, если внешнее воздействие приложено, как показано на рис. а), то его можно перенести по цепи вперед, добавив передаточную функцию тех звеньев, через которые сделан перенос , рис. в).
При переносе внешнего воздействия f по цепи назад следует добавлять передаточную функцию, обратную передаточной функции звеньев, через которые сделан перенос

Структурные преобразования

Структурные преобразования
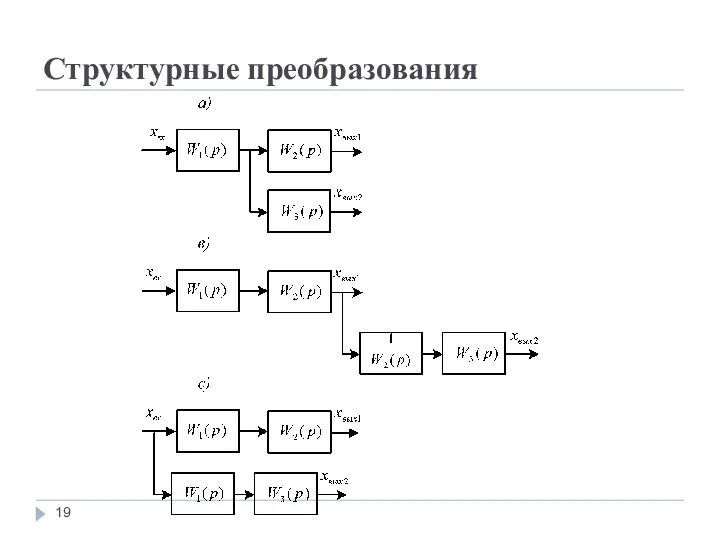
3. Последовательно соединенные звенья можно, согласно с формулой (1), менять местами без изменения общей передаточной функции цепи.
4. Можно производить перенос звена параллельно контура вперед или назад по цепи с соответствующими добавлениями.
На рис.,a) приведен пример переноса звена параллельно контура вперед (рис.в)) и назад (рис.с)) по цепи.

Структурные преобразования

Структурные преобразования
Причем при параллельном переносе звена вперед по цепи, необходимо добавить передаточную функцию, обратную передаточной функции звеньев, через которые был сделан перенос
А при параллельном переносе звена назад по цепи, необходимо добавить передаточную функцию тех звеньев, через которые был сделан перенос

Структурные преобразования
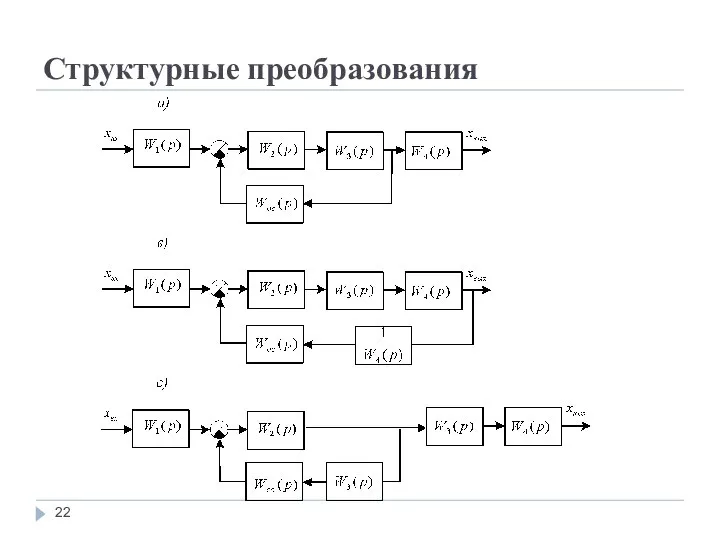
Руководствуясь правилами п.4. можно переносить место включения цепи обратной связи вперед или назад параллельно контура.
Пример приведен на рис.а), рис.,в) – перенос вперед, рис.,с) – перенос назад).

Структурные преобразования

Структурные преобразования
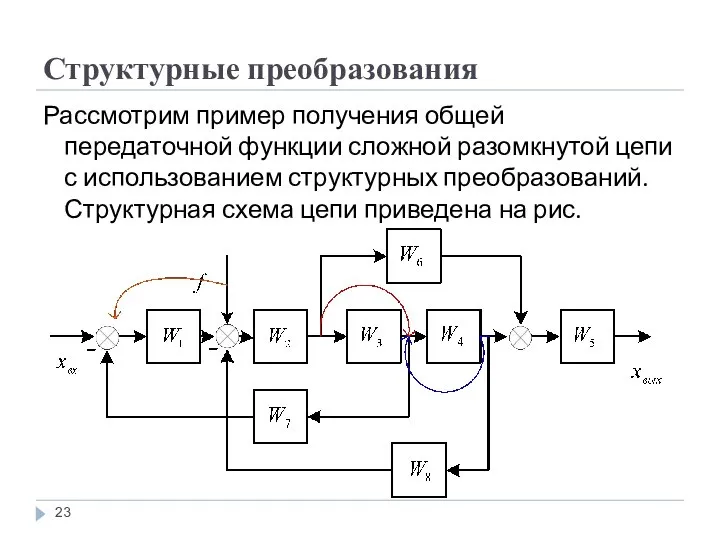
Рассмотрим пример получения общей передаточной функции сложной разомкнутой цепи с использованием структурных преобразований. Структурная схема цепи приведена на рис.

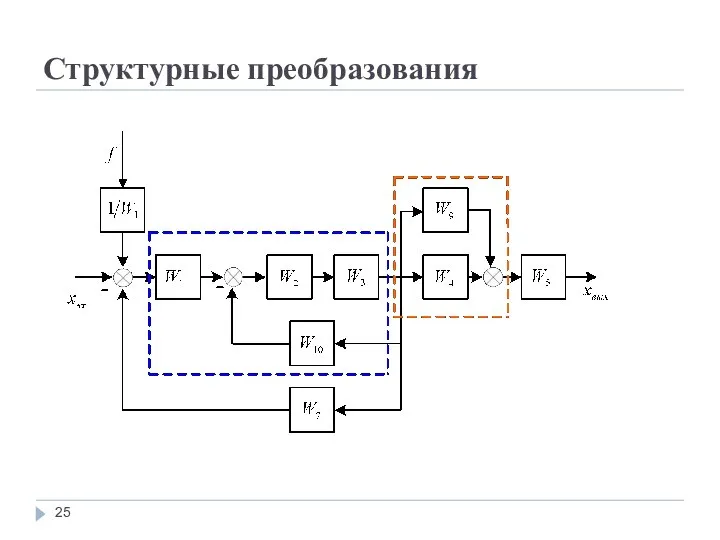
Структурные преобразования
Первый шаг преобразования показан на рис., где согласно правилам п.4. и п.5., имеем
и, кроме того, по правилу п.2. сделан перенос назад внешнего воздействия f.

Структурные преобразования

Структурные преобразования
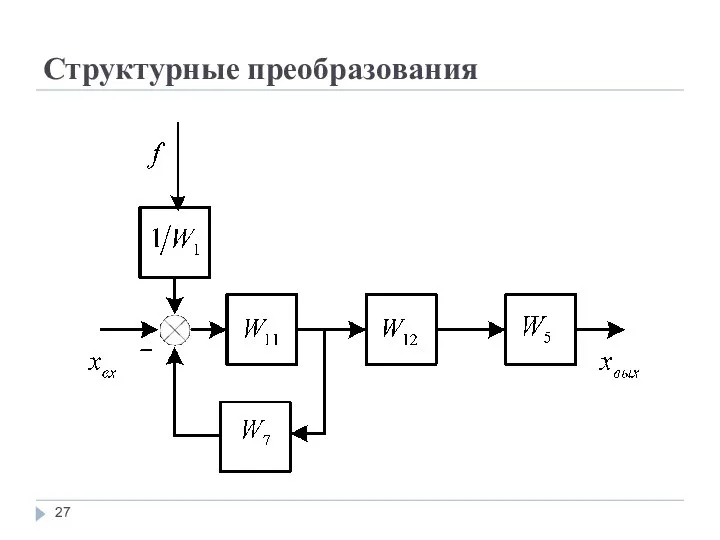
Второй шаг преобразования изображен на рис., где согласно правилу п.1. получим

Структурные преобразования

Структурные преобразования
Наконец, на основании схемы рис. находим окончательно общее выражение передаточной функции всей разомкнутой цепи по каждому из двух входных воздействий отдельно