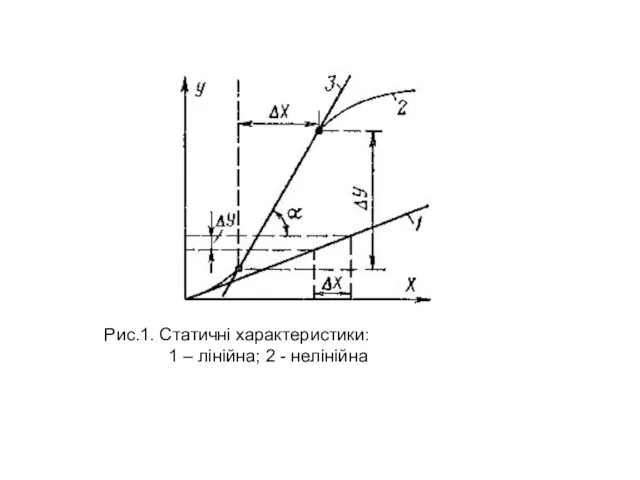
Слайд 2Рис.1. Статичні характеристики:
1 – лінійна; 2 - нелінійна
Слайд 3Передаточний коефіцієнт k є основним параметром, який характеризує роботу системи або ланки

в сталому режимі, і визначається із статичної характеритики .
При послідовному з’єднанні ланок
При паралельному з’єднанні ланок
Для ланок, охоплених зворотнім зв’язком
Слайд 4х х
х(t) t
1(t)
t
Типові зовнішні дії:
а – одинична; б
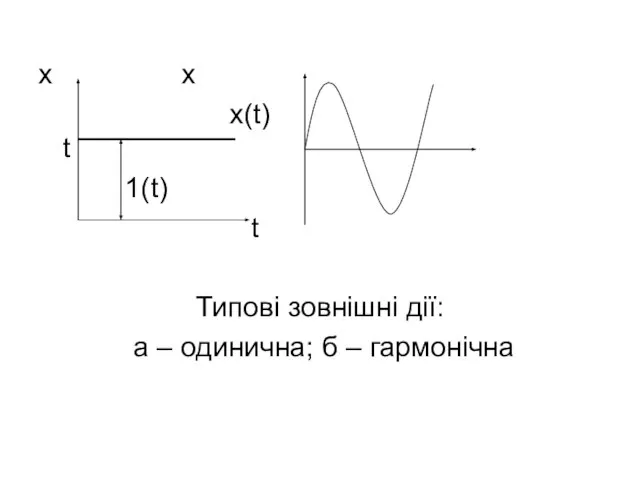
– гармонічна
Слайд 5 Перетворення Лапласа
Приклад

Слайд 6Передаточна функція W(р) – відношення зображення вихідної величини ланки до зображення вхідної
.
Якщо

замінити р на jω, то отримаємо частотну передаточну функцію
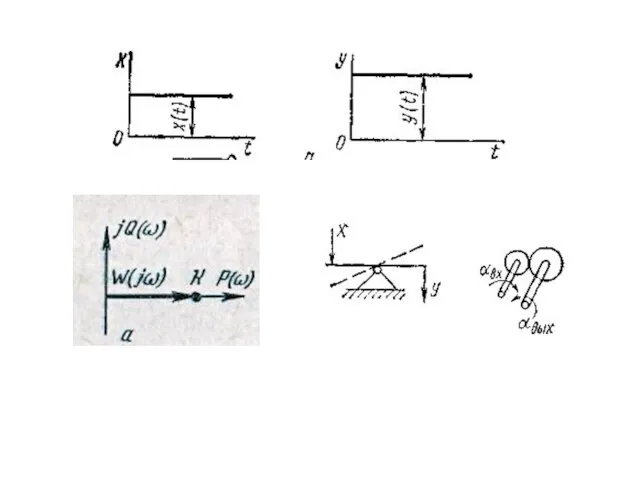
Слайд 7 Амплітудо-частотна характеристика – залежність відношення амплітуди Авих(ωі) коливань гармонічної дії на

виході до амплітуди Авх(ωі) коливань на вході від частоти коливань ωі
Фазо-частотна характеристика – залежність кута зсуву фаз від частоти
Амплітудо-фазо-частотна характеристика – залежність передаточної функції від частоти
Слайд 8Безінерційна (підсилювальна)
(к – передаточний коефіцієнт)

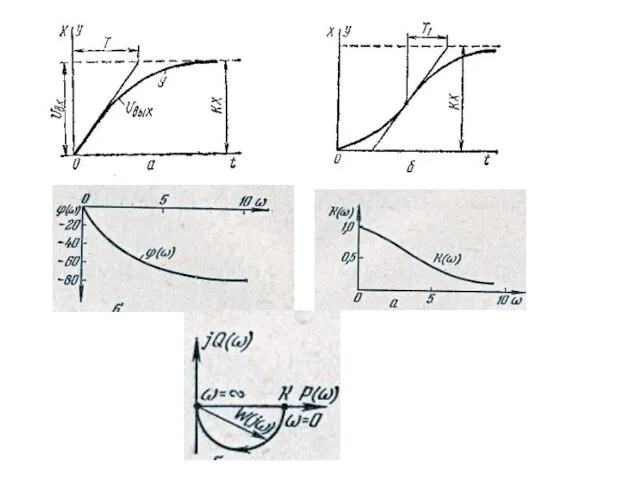
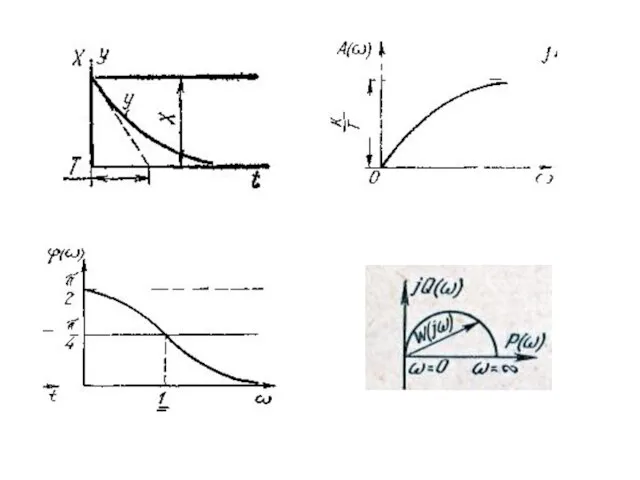
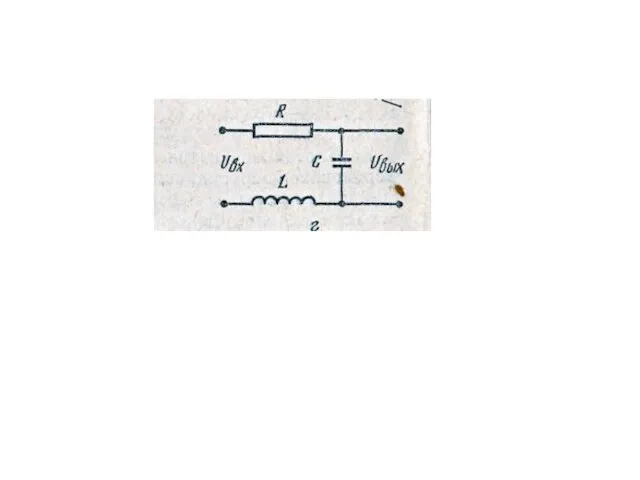
Слайд 10Аперіодична ланка І порядку
W(p)=

Слайд 11Аперіодична ланка ІІ порядку (послідовне з’єднання двох аперіодичних ланок першого порядку за

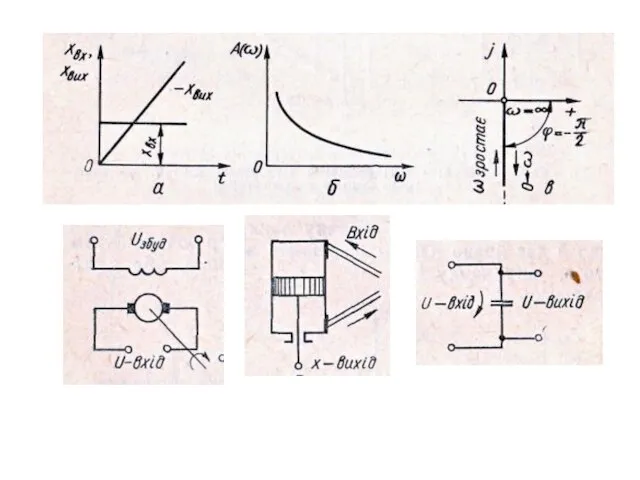
Слайд 13Диференціююча
Ідеальна
W(p)=
Реальна
W(p)=

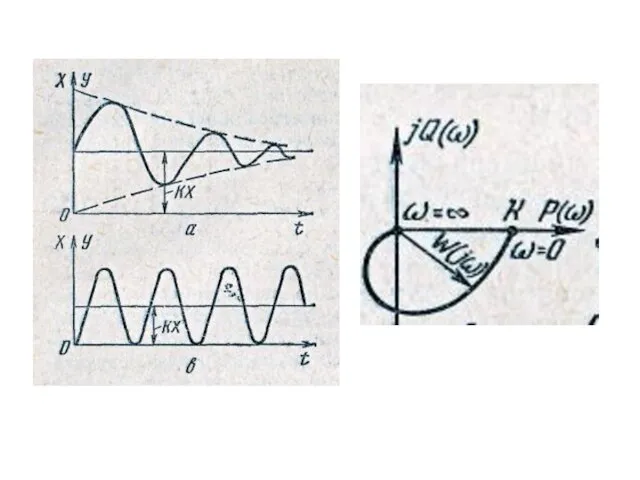
Слайд 17Коливальна
Стійка
W(p)=
Нестійка
W(p)=















 Тема урока:Прикладная среда графического редактора Paint.
Тема урока:Прикладная среда графического редактора Paint. Презентация на тему Система национальных счетов
Презентация на тему Система национальных счетов Двадцатилетний брак великого князя Московского Василия III с Соломонией Сабуровой был бесплоден. Отправив законную жену в монастыр
Двадцатилетний брак великого князя Московского Василия III с Соломонией Сабуровой был бесплоден. Отправив законную жену в монастыр Cn(H2O)m
Cn(H2O)m 20140111_prezentatsiya_k_igre
20140111_prezentatsiya_k_igre Умей предупреждать болезни
Умей предупреждать болезни Еженедельное совещание. Статус работ блока Геология и разработка
Еженедельное совещание. Статус работ блока Геология и разработка Изделие Святой Николаус-Чудотворец
Изделие Святой Николаус-Чудотворец Среднее арифметическое, мода и размах ряда.
Среднее арифметическое, мода и размах ряда. Амплуа игроков в волейболе и их функции
Амплуа игроков в волейболе и их функции Страховые представители АО Страховая компания СОГАЗ-Мед
Страховые представители АО Страховая компания СОГАЗ-Мед «EVA 2011 Москва» 28 – 30 ноября 2011 Сбор и долговременное сохранение электронной информации в сфере культуры. Л.А. Куйбышев, Н.В. Браккер,
«EVA 2011 Москва» 28 – 30 ноября 2011 Сбор и долговременное сохранение электронной информации в сфере культуры. Л.А. Куйбышев, Н.В. Браккер,  Диего Веласкес. Сдача Бреды 1634–1635
Диего Веласкес. Сдача Бреды 1634–1635 К НЕМУ НЕ ЗАРАСТЕТНАРОДНАЯ ТРОПА А. С. Пушкину посвящается…
К НЕМУ НЕ ЗАРАСТЕТНАРОДНАЯ ТРОПА А. С. Пушкину посвящается… тема: «Воображение как общая способность»
тема: «Воображение как общая способность»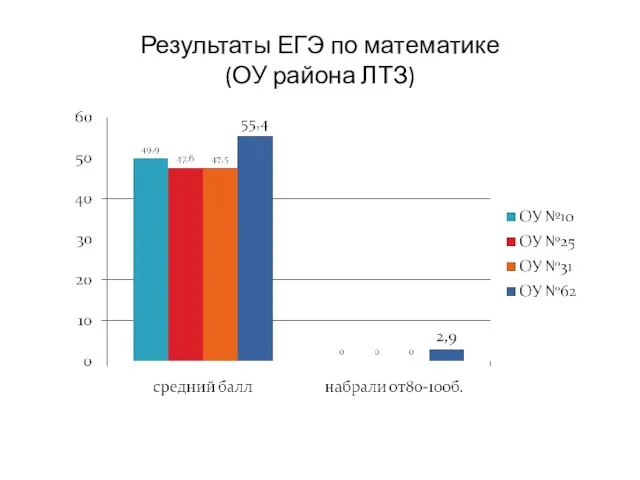 Результаты ЕГЭ по математике (ОУ района ЛТЗ)
Результаты ЕГЭ по математике (ОУ района ЛТЗ) Качество влияния личности на ход истории (на примере А. Гитлера и И. Сталина)
Качество влияния личности на ход истории (на примере А. Гитлера и И. Сталина) Организация обучения учителей по курсу «Основы религиозных культур и светской этики» в Калининградской области
Организация обучения учителей по курсу «Основы религиозных культур и светской этики» в Калининградской области ООО Глобал Контейнер Лоджистикс
ООО Глобал Контейнер Лоджистикс Жак Рене Ширак
Жак Рене Ширак Игра в слова
Игра в слова Бизнес-план Пончиковой
Бизнес-план Пончиковой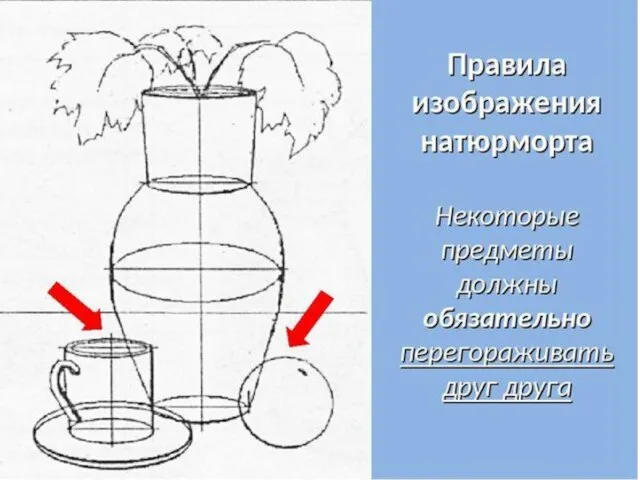 Занятие 3 года обучения на каникулах. Декоративный натюрморт
Занятие 3 года обучения на каникулах. Декоративный натюрморт Лабораторная группаРезультаты серологического этапа ДЭН выводы, задачи2008 год
Лабораторная группаРезультаты серологического этапа ДЭН выводы, задачи2008 год Виды наказаний
Виды наказаний Ультразвуковой датчик
Ультразвуковой датчик Легенды театральной сцены
Легенды театральной сцены ПОДПИСКА
ПОДПИСКА