Парадоксы бесконечности

Ахиллес и черепаха
Расстояние между Ахиллесом и черепахой 1 км. Скорость Ахиллеса в 10 раз больше скорости черепахи. Догонит ли Ахиллес черепаху?

Сколько ангелов помещается на конце иглы?

Каких натуральных чисел больше: четных или нечетных?
Каких чисел больше: четных натуральных или всех натуральных чисел?
Каких чисел больше: натуральных или целых?
Где точек больше: на отрезке в 1 см или 1 м?
Где точек больше: на отрезке в 1 см или на прямой?

Занумеруем множество четных чисел
2, 4, 6, 8, 10, 12, …
1 2 3 4 5 6 …
Взаимно однозначное соответствие
Номер:
Говорят, что между множествами установили взаимно однозначное соответствие

Примеры взаимно однозначных соответствий
множество государств Европы – множество столиц европейских государств;
множество автомобилей – множество их номеров;
множество страниц в книге – множество их номеров;
множество предметов в витрине – множество их цен.

Множество простых чисел
2, 3, 5, 7, 11, 13, 17, 19, …
1 2 3 4 5 6 7 8 …
Счетные множества
Номер:
Бесконечное множество А называется счетным, если его элементы можно перенумеровать (или поставить во взаимно однозначное соответствие со множеством натуральных чисел).

Счетно ли множество
целых чисел?
…, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …
… 9 7 5 3 1 2 4 6 8 10 …
Вывод: целых чисел столько же, сколько
и натуральных, и целых, и простых.
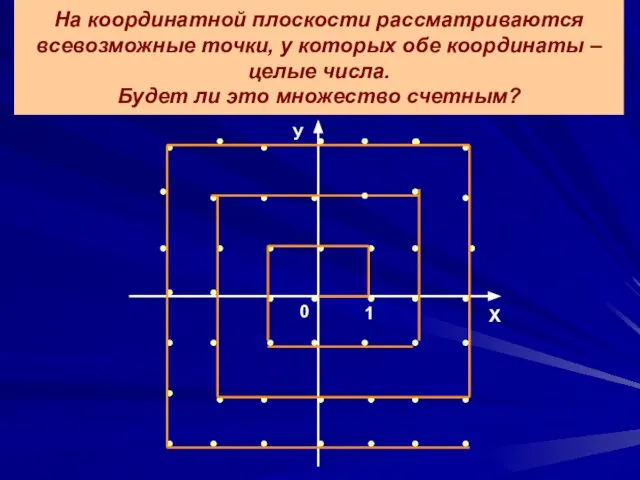
Говорят: такие множества имеют одинаковую мощность

На координатной плоскости рассматриваются всевозможные точки, у которых обе координаты – целые числа.
Будет ли это множество счетным?
Х
У
0
1

Не все бесконечные множества можно перенумеровать. Например:
множество действительных чисел;
множество точек отрезка;
множество точек прямой и т.п.
Такие множества называются несчетными
Несчетные множества

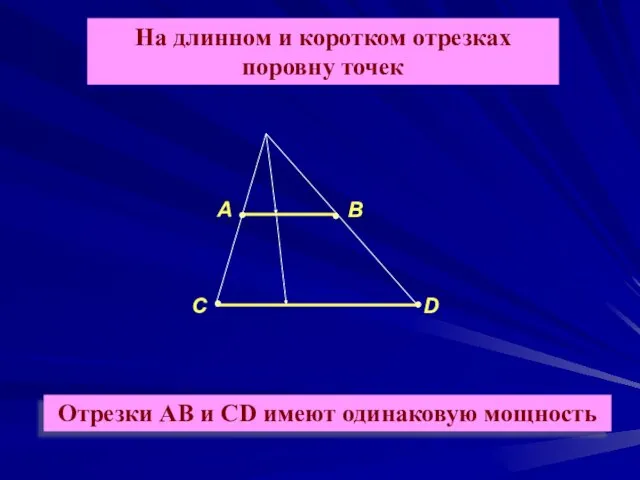
Отрезки АВ и СD имеют одинаковую мощность
На длинном и коротком отрезках поровну точек

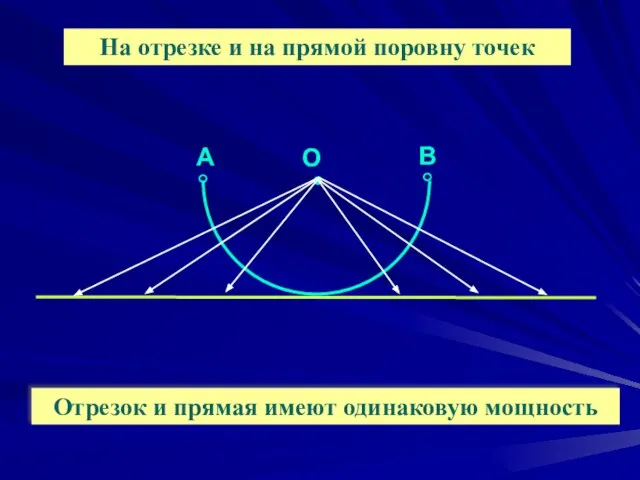
Отрезок и прямая имеют одинаковую мощность
На отрезке и на прямой поровну точек
А
В
О

Необыкновенная гостиница

Задача №1
1, 2, 3, 4, 5, 6, 7, …
1, 2, 3, 4, 5, 6, 7, 8, …
Задача №2
1, 2, 3, 4, 5, 6, 7, …, n, …
2, 4, 6, 8,10,12,14,…, 2n,…