Содержание
- 2. Аннотация 1. Линейная обратная задача гравиметрии о нахождении плотности в слое. Для решения линейной обратной задачи
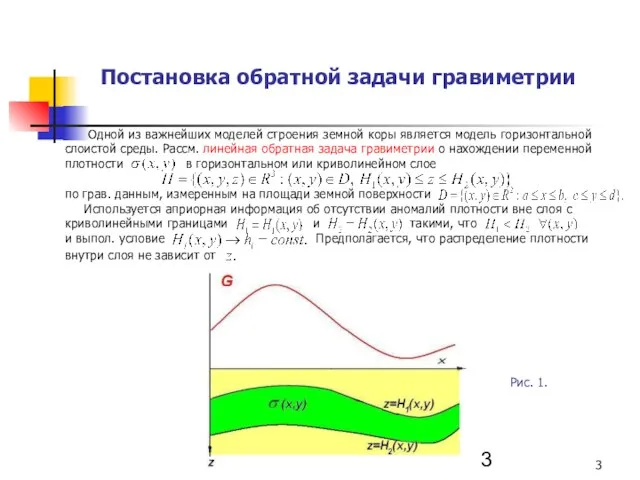
- 3. Постановка обратной задачи гравиметрии Одной из важнейших моделей строения земной коры является модель горизонтальной слоистой среды.
- 4. Нахождение плотности в слое Задача сводится к решению линейного двумерного интегрального уравнения Фредгольма первого рода для
- 5. Методы решения После дискретизации уравнения (1) на сетке где задана правая часть и аппроксимации интегрального оператора
- 6. Методы решения СЛАУ 1. Итеративно регуляризованный метод простой итерации (МПИ) где макс. собств. значение 2. Метод
- 7. Параллельная реализация на МВС-1000 Ранее для решения линейной обратной задачи гравиметрии о восстановлении переменной плотности в
- 8. Рис. 2. Схема распределения данных по процессорам Комплекс параллельных численных алгоритмов реализован с помощью библиотеки MPI
- 9. На МВС-1000/64 решена задача с реальными данными о восстановлении плотности в горизонтальном слое между глубинами для
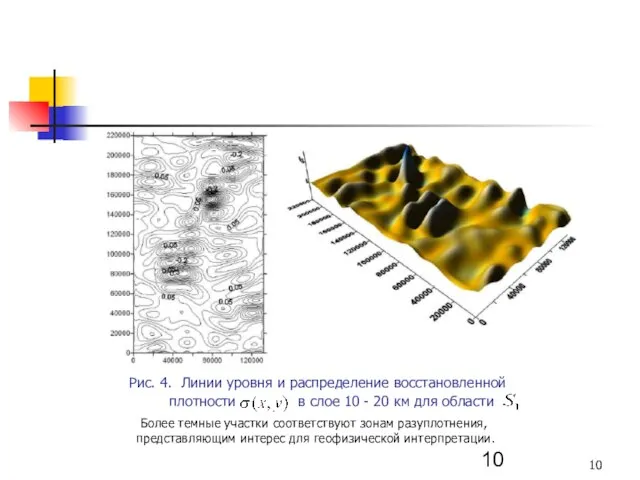
- 10. Рис. 4. Линии уровня и распределение восстановленной плотности в слое 10 - 20 км для области
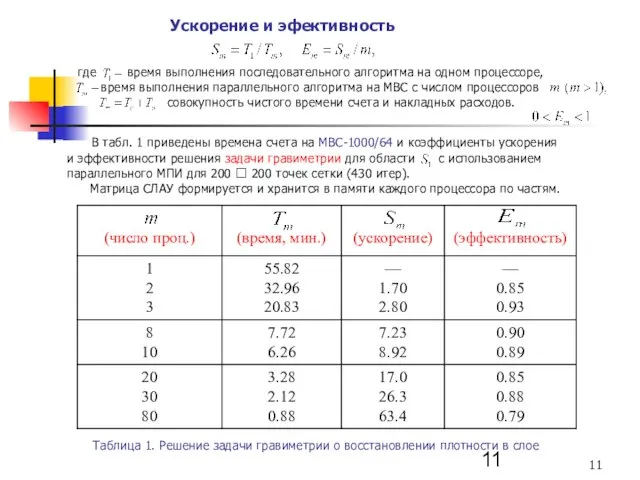
- 11. В табл. 1 приведены времена счета на МВС-1000/64 и коэффициенты ускорения и эффективности решения задачи гравиметрии
- 12. Распараллеливание на видеоускорителях с помощью технологии CUDA http://www.nvidia.ru Для организации параллельных вычислений актуальным в настоящее время
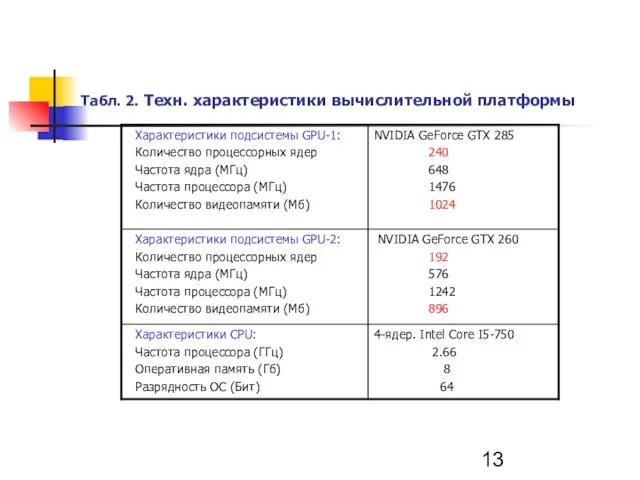
- 13. Табл. 2. Техн. характеристики вычислительной платформы
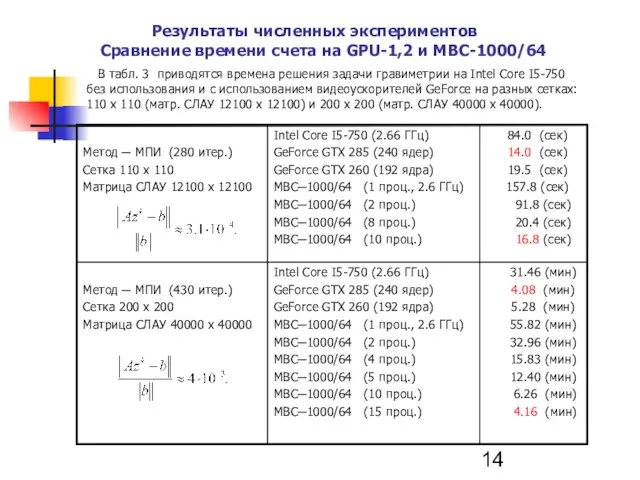
- 14. В табл. 3 приводятся времена решения задачи гравиметрии на Intel Core I5-750 без использования и с
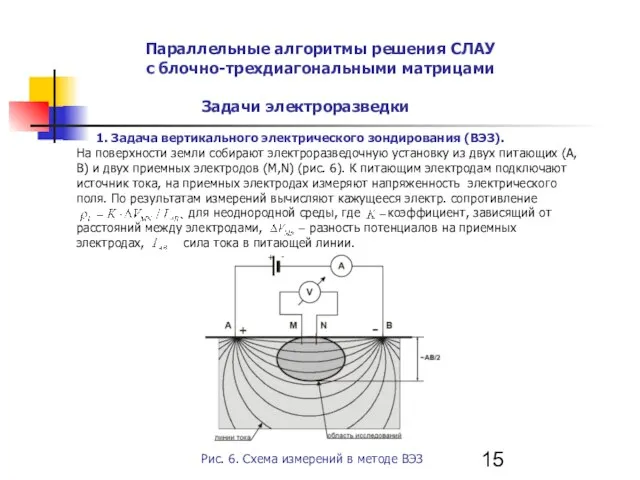
- 15. Параллельные алгоритмы решения СЛАУ с блочно-трехдиагональными матрицами Задачи электроразведки 1. Задача вертикального электрического зондирования (ВЭЗ). На
- 16. 1. Задача ВЭЗ о нахождении потенциала на поверхности земли сводится к решению двумерного уравнения Лапласа в
- 17. где и искомые и заданные векторы размерности n, квадратные матрицы порядка n. Будем предполагать, что исходная
- 18. где и квадратные матрицы порядка n. Схема параллельного алгоритма матричной прогонки: (10)-(11)-(12) → (14) → (13).
- 19. Для СЛАУ (15) МСГ с предобуславливателем имеет вид [12] 2. Параллельный метод сопряженных градиентов с предобуславливателем
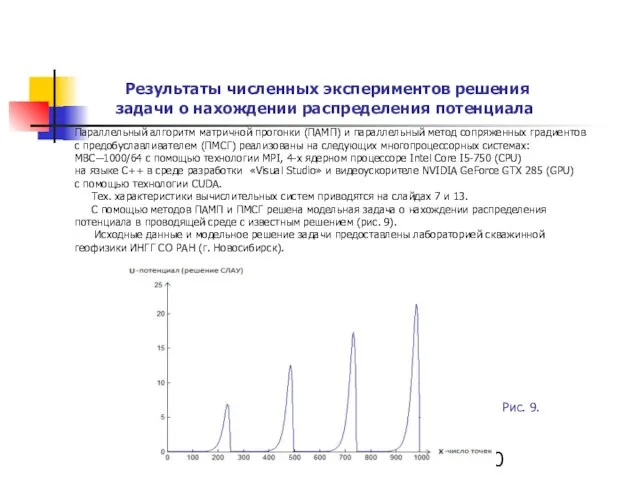
- 20. Параллельный алгоритм матричной прогонки (ПАМП) и параллельный метод сопряженных градиентов с предобуславливателем (ПМСГ) реализованы на следующих
- 21. После дискретизации задача сводится к СЛАУ с плохо обусловленной симметричной положительно-определенной блочно-трехдиагональной матрицей размерности c квадратными
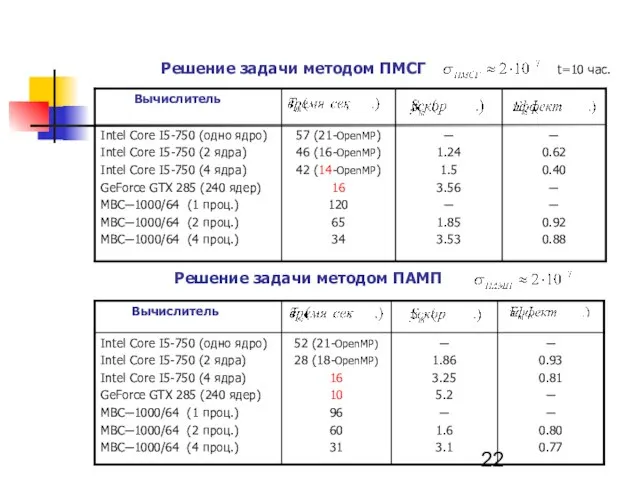
- 22. Решение задачи методом ПМСГ t=10 час. Решение задачи методом ПАМП
- 23. Основные результаты работы 1. Для решения линейной обратной задачи гравиметрии о восстановлении плотности в слое предложены
- 25. Скачать презентацию











![Для СЛАУ (15) МСГ с предобуславливателем имеет вид [12] 2. Параллельный метод](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/391065/slide-18.jpg)


 Построение плана и разреза горного отвода, расчет годовой мощности и срока службы шахты (уголь)
Построение плана и разреза горного отвода, расчет годовой мощности и срока службы шахты (уголь) Рубенс Питер Пауль (1577-1640)
Рубенс Питер Пауль (1577-1640) Основы проектной деятельности
Основы проектной деятельности Субъекты Российской Федерации
Субъекты Российской Федерации Родительское собрание
Родительское собрание Достопримечательности Московского Кремля
Достопримечательности Московского Кремля Формы организации познавательной деятельности учащихся
Формы организации познавательной деятельности учащихся Системы развития подростков: сервисы, курсы, консалтинг, сообщества
Системы развития подростков: сервисы, курсы, консалтинг, сообщества Статистический метод определения авторства художественного текста
Статистический метод определения авторства художественного текста ЦЕНТР мониторинга морских биоинвазий и балластных вод при Институте биологии моря им. А.В. Жирмунского
ЦЕНТР мониторинга морских биоинвазий и балластных вод при Институте биологии моря им. А.В. Жирмунского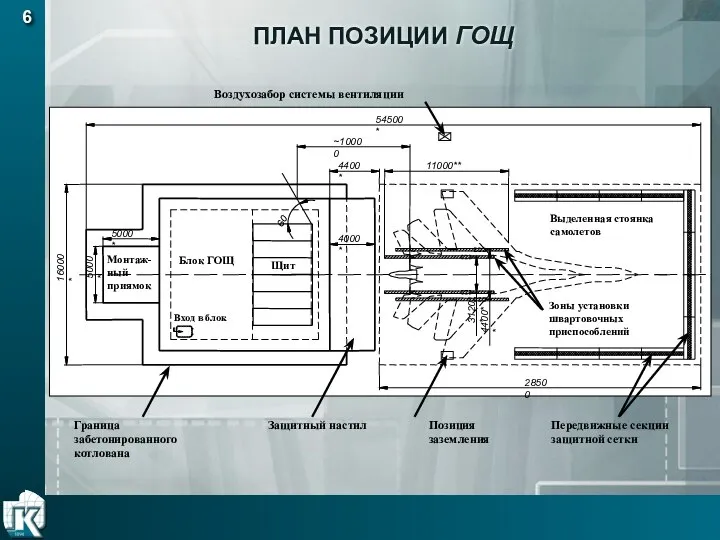 План позиции гощ
План позиции гощ Комплексный подход к автоматизации учета энергоресурсов
Комплексный подход к автоматизации учета энергоресурсов Презентация на тему Мультимедиа технологии
Презентация на тему Мультимедиа технологии  Лекція 1_2021
Лекція 1_2021 Алгебра.8класс.Квадратные уравнения.Определение квадратного уравнения.Неполные квадратные уравнения
Алгебра.8класс.Квадратные уравнения.Определение квадратного уравнения.Неполные квадратные уравнения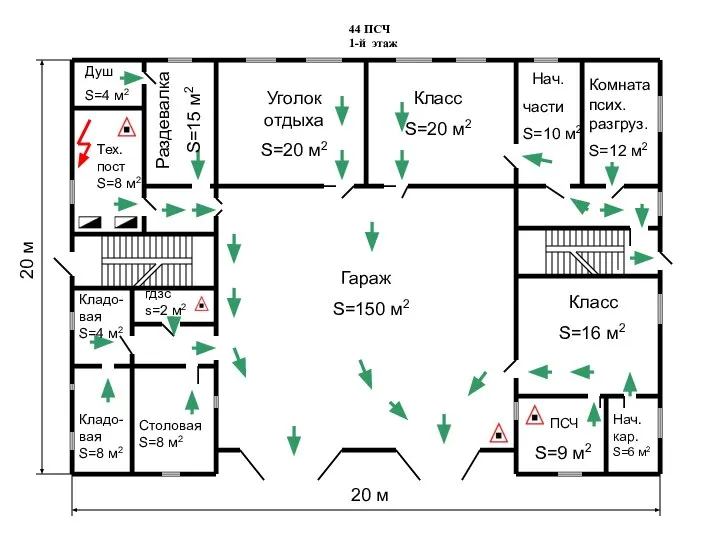 44 ППЧ
44 ППЧ Краснодарский чай
Краснодарский чай Модель фирмы на конкурентных рынках
Модель фирмы на конкурентных рынках Таможенные пошлины. Тема 1.4
Таможенные пошлины. Тема 1.4 Климат моей квартиры
Климат моей квартиры Великие географические открытия 7 класс
Великие географические открытия 7 класс мир худ.кул.просвещения (3)
мир худ.кул.просвещения (3) ПРИМЕРЫ ОРГАНИЗАЦИИ РЕАГИРОВАНИЯ ЭКСТРЕННЫХ ОПЕРАТИВНЫХ СЛУЖБ ПРИ ВЫЗОВАХ ОТ НАСЕЛЕНИЯ ПО ЕДИНОМУ НОМЕРУ «112»
ПРИМЕРЫ ОРГАНИЗАЦИИ РЕАГИРОВАНИЯ ЭКСТРЕННЫХ ОПЕРАТИВНЫХ СЛУЖБ ПРИ ВЫЗОВАХ ОТ НАСЕЛЕНИЯ ПО ЕДИНОМУ НОМЕРУ «112» Первичная и вторичная профилактика инсульта с позиций доказательной медицины
Первичная и вторичная профилактика инсульта с позиций доказательной медицины Принципы применения права Европейского Союза
Принципы применения права Европейского Союза Выполнила : Выполнила : ученица 9«б»класса МАОУ СОШ№ 15 г. Челябинска Назарова Елена . Руководитель: Левина Светлана Владимиров
Выполнила : Выполнила : ученица 9«б»класса МАОУ СОШ№ 15 г. Челябинска Назарова Елена . Руководитель: Левина Светлана Владимиров Развитие информационной среды образовательного учреждения - необходимое условие реализации ФГОС
Развитие информационной среды образовательного учреждения - необходимое условие реализации ФГОС Мой современник. АНО ДО Параллели
Мой современник. АНО ДО Параллели