Слайд 2Структурная схема
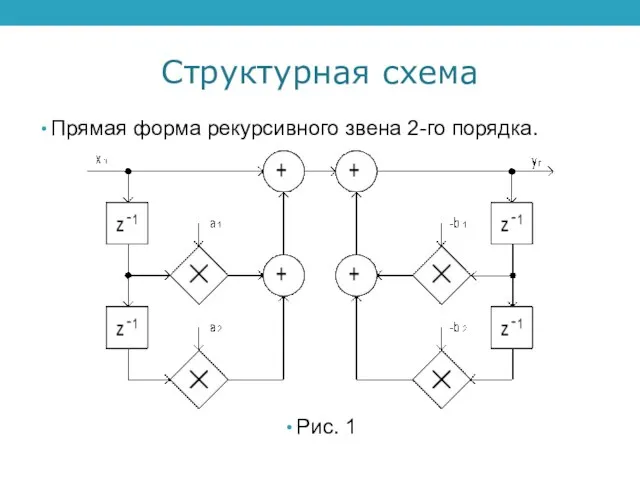
Прямая форма рекурсивного звена 2-го порядка.
Рис. 1
Слайд 3Структурная схема
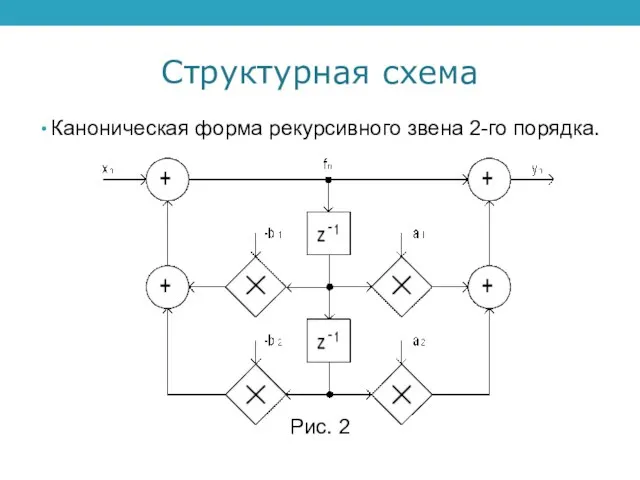
Каноническая форма рекурсивного звена 2-го порядка.
Рис. 2
Слайд 4Передаточная функция
Воспользовавшись формулой (10) для АЧХ нерекурсивного звена 2-го порядка, запишем по

аналогии выражение для АЧХ исследуемого рекурсивного звена 2-го порядка:
(4)
Слайд 5Передаточная функция
Точно так же, воспользовавшись формулой (12) для вычисления АЧХ НЦФ 2-го

порядка через расстояния от точки ejωT до нулей передаточной функции НЦФ, запишем по аналогии
(5),
где ρ0i – расстояние от точки ejωT до i-го нуля передаточной функции,
а ρpi – расстояние от точки ejωT до i-го полюса передаточной функции ЦФ.




 совместно с Театром праздника «Солнечный зайчик»
совместно с Театром праздника «Солнечный зайчик» ЧАС ЗАНИМАТЕЛЬНОЙ БИОЛОГИИ 7 класс
ЧАС ЗАНИМАТЕЛЬНОЙ БИОЛОГИИ 7 класс Презентация на тему Врожденные и приобретенные программы поведения
Презентация на тему Врожденные и приобретенные программы поведения Презентация
Презентация ПРОЕКТНАЯ РАБОТА
ПРОЕКТНАЯ РАБОТА к.э.н. директор Бизнес- инкубатора, заместитель проректора по инновационной деятельности УрФУ Пиличев Валерий Валерьевич
к.э.н. директор Бизнес- инкубатора, заместитель проректора по инновационной деятельности УрФУ Пиличев Валерий Валерьевич Культура Руси в 10 – 13 веках
Культура Руси в 10 – 13 веках Болгария в 20-30-е годы
Болгария в 20-30-е годы Доказательная медицина и доказательная педагогика. Взгляд врача и исследователя
Доказательная медицина и доказательная педагогика. Взгляд врача и исследователя Приготовление завтрака
Приготовление завтрака «Инвестиционная политика муниципального образования на современном этапе»02.02.2012
«Инвестиционная политика муниципального образования на современном этапе»02.02.2012 Работа академии по направлению научно-технического творчества молодежи
Работа академии по направлению научно-технического творчества молодежи «Трудные» дети и их проблемы.
«Трудные» дети и их проблемы. Приемы расположения к себе. Самопрезентация
Приемы расположения к себе. Самопрезентация Автохимия. Завод автохимии
Автохимия. Завод автохимии Об итогах выполнения задач в ЗПО 2017 учебного года и постановка задач на ЛПО 2017 учебного года
Об итогах выполнения задач в ЗПО 2017 учебного года и постановка задач на ЛПО 2017 учебного года Евангелие от Матфея
Евангелие от Матфея Нарушения требований Федерального закона от 20.07.2012 № 125-ФЗ О донорстве крови и ее компонентов
Нарушения требований Федерального закона от 20.07.2012 № 125-ФЗ О донорстве крови и ее компонентов Аварийная аптечка для первой медицинской помощи
Аварийная аптечка для первой медицинской помощи Власть. Сила. Лекция 2
Власть. Сила. Лекция 2 Вітражі та шпроси
Вітражі та шпроси Моя будущая профессия - бухгалтер
Моя будущая профессия - бухгалтер Олимпиада үрләренә - баскычлап
Олимпиада үрләренә - баскычлап Общероссийские антидопинговые правила
Общероссийские антидопинговые правила Проектирование транспортно-грузовых комплексов
Проектирование транспортно-грузовых комплексов Определение размеров молекул октана
Определение размеров молекул октана Такси Лось
Такси Лось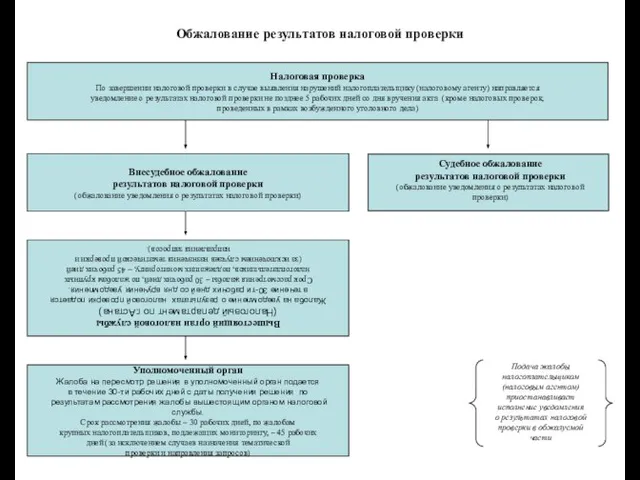 Обжалование результатов налоговой проверки
Обжалование результатов налоговой проверки