Пересечение плоскостей. Пересечение прямой и проецирующей плоскости

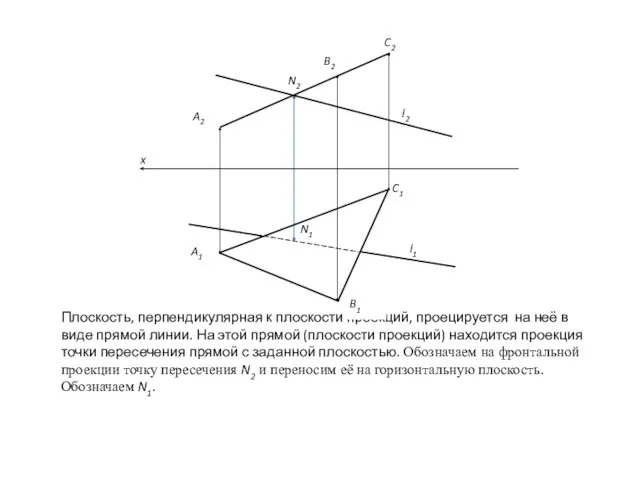
Плоскость, перпендикулярная к плоскости проекций, проецируется на неё в виде прямой линии. На этой прямой (плоскости проекций) находится проекция точки пересечения прямой с заданной плоскостью. Обозначаем на фронтальной проекции точку пересечения N2 и переносим её на горизонтальную плоскость. Обозначаем N1.
N2
N1

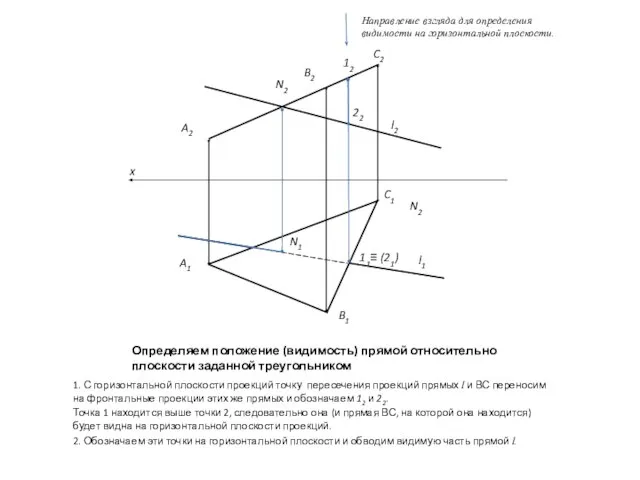
Определяем положение (видимость) прямой относительно плоскости заданной треугольником
1. С горизонтальной плоскости проекций точку пересечения проекций прямых l и ВС переносим на фронтальные проекции этих же прямых и обозначаем 12 и 22.
Точка 1 находится выше точки 2, следовательно она (и прямая ВС, на которой она находится) будет видна на горизонтальной плоскости проекций.
2. Обозначаем эти точки на горизонтальной плоскости и обводим видимую часть прямой l.
N2
N1
12
22
11≡ (21)
N2
Направление взгляда для определения видимости на горизонтальной плоскости.

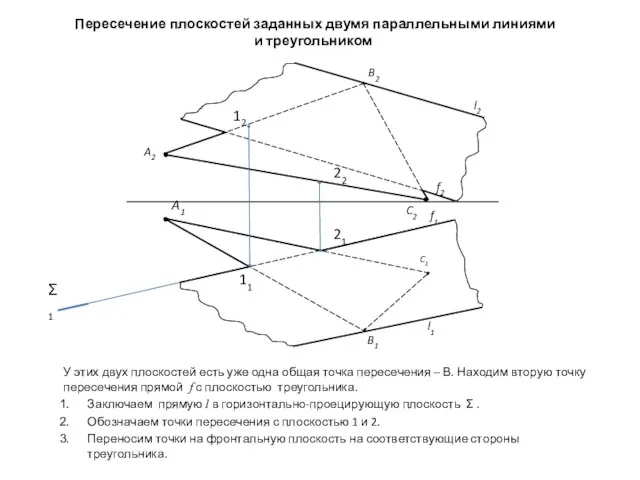
Пересечение плоскостей заданных двумя параллельными линиями и треугольником
У этих двух плоскостей есть уже одна общая точка пересечения – В. Находим вторую точку пересечения прямой f с плоскостью треугольника.
Заключаем прямую l в горизонтально-проецирующую плоскость Σ .
Обозначаем точки пересечения с плоскостью 1 и 2.
Переносим точки на фронтальную плоскость на соответствующие стороны треугольника.
Σ1
21
11
12
22

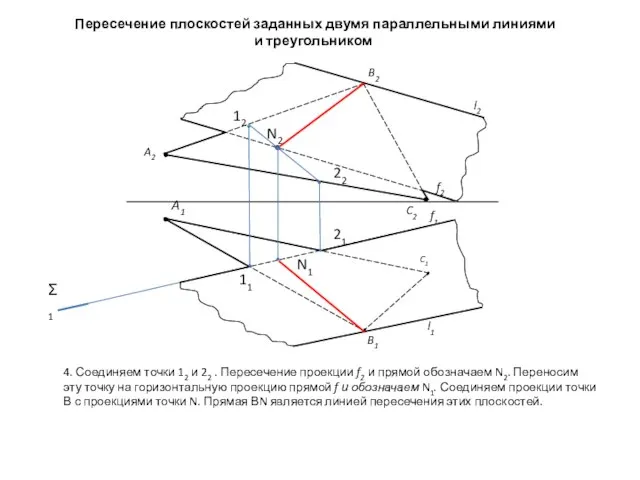
Пересечение плоскостей заданных двумя параллельными линиями и треугольником
4. Соединяем точки 12 и 22 . Пересечение проекции f2 и прямой обозначаем N2. Переносим эту точку на горизонтальную проекцию прямой f и обозначаем N1. Соединяем проекции точки В с проекциями точки N. Прямая ВN является линией пересечения этих плоскостей.
Σ1
21
11
12
22
N2
N1

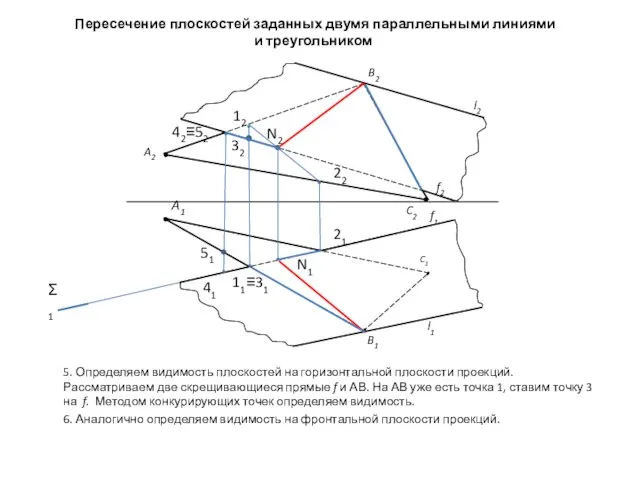
Пересечение плоскостей заданных двумя параллельными линиями и треугольником
5. Определяем видимость плоскостей на горизонтальной плоскости проекций. Рассматриваем две скрещивающиеся прямые f и АВ. На АВ уже есть точка 1, ставим точку 3 на f. Методом конкурирующих точек определяем видимость.
6. Аналогично определяем видимость на фронтальной плоскости проекций.
Σ1
21
11≡31
12
22
N2
N1
32
42≡52
51
41

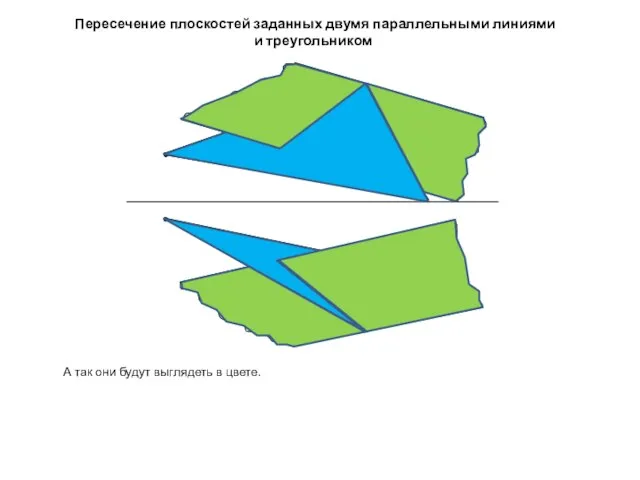
Пересечение плоскостей заданных двумя параллельными линиями и треугольником
А так они будут выглядеть в цвете.

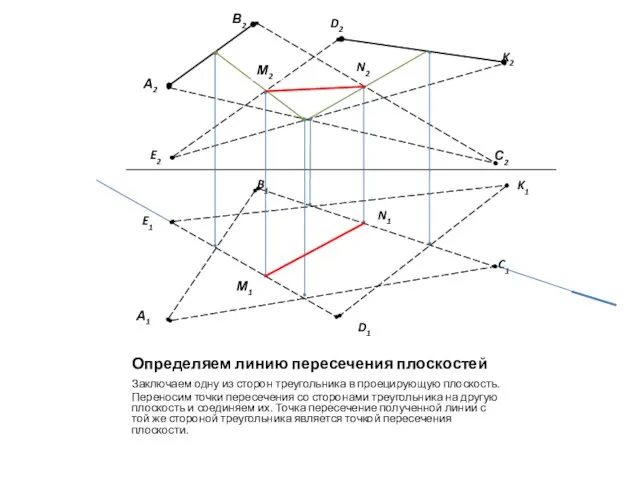
Определяем линию пересечения плоскостей
Заключаем одну из сторон треугольника в проецирующую плоскость.
Переносим точки пересечения со сторонами треугольника на другую плоскость и соединяем их. Точка пересечение полученной линии с той же стороной треугольника является точкой пересечения плоскости.
D1
N1
N2
М1
М2

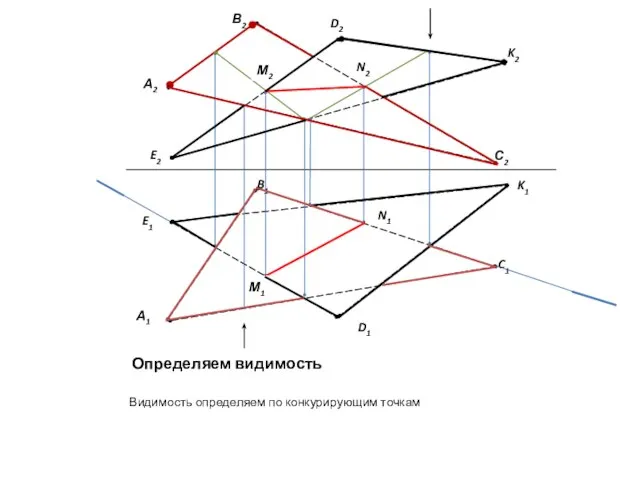
Определяем видимость
Видимость определяем по конкурирующим точкам
D1
N1
N2
М1
М2