Содержание
- 2. Пригадаємо… π 0
- 3. Подумайте Що спільного між кутами: -3300 300 3900 7500 11400 -6900 = 300-1∙3600 = 300-2∙3600 =
- 4. Періоди функцій Для будь-якого кута α: 1) sin α = sin(α+2π) 2) cos α = cos(α+2π)
- 5. Правила знаходження періодів функцій Сінус або косинус Тангенс або котангенс х =2π T Відповідь: T =
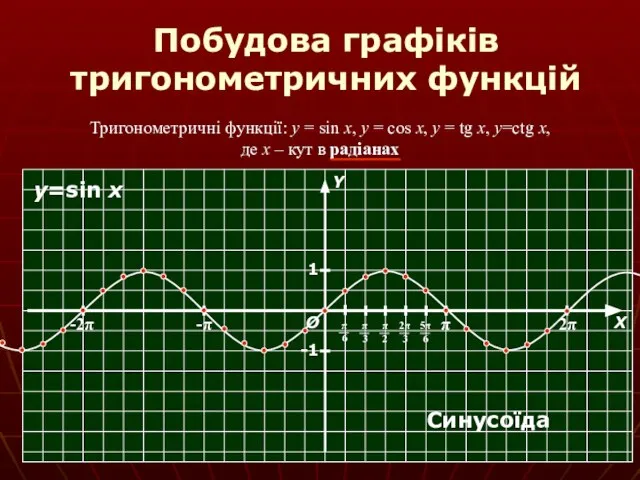
- 6. Побудова графіків тригонометричних функцій Тригонометричні функції: y = sin x, y = cos x, y =
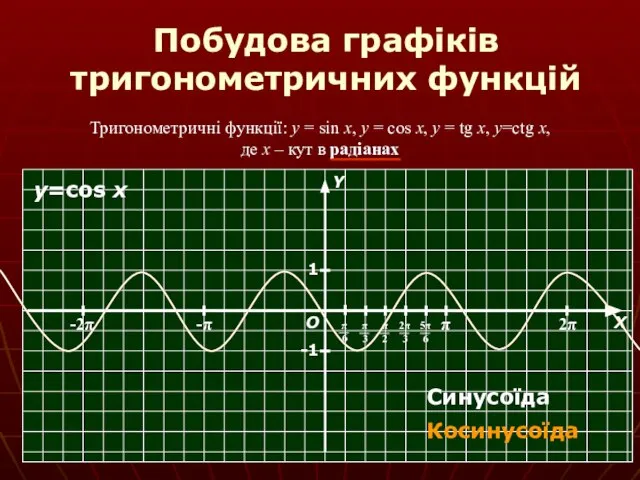
- 7. Побудова графіків тригонометричних функцій Тригонометричні функції: y = sin x, y = cos x, y =
- 9. Скачать презентацию




 Борьба с компьютерными вирусами при работе на ПК
Борьба с компьютерными вирусами при работе на ПК Кредо. Шаблон
Кредо. Шаблон КОНКРЕТНОЕ СОЦИОЛОГИЧЕСКОЕ ИССЛЕДОВАНИЕ( КСИ ).
КОНКРЕТНОЕ СОЦИОЛОГИЧЕСКОЕ ИССЛЕДОВАНИЕ( КСИ ). Пословицы и поговорки о труде
Пословицы и поговорки о труде Мы из будущего! Марафон проектов как игра
Мы из будущего! Марафон проектов как игра Чертежи. Изображения - виды
Чертежи. Изображения - виды Презентация на тему НИКОЛАЙ ВАСИЛЬЕВИЧ ГОГОЛЬ 1809-1852
Презентация на тему НИКОЛАЙ ВАСИЛЬЕВИЧ ГОГОЛЬ 1809-1852  Автор: учитель биологии Егоров Сергей Владимирович (Еласовская средняя общеобразовательная школа Горномарийского района республ
Автор: учитель биологии Егоров Сергей Владимирович (Еласовская средняя общеобразовательная школа Горномарийского района республ Радуга основных категорий планирования
Радуга основных категорий планирования Математическая статистика
Математическая статистика Электронные таблицы. Термины и понятия
Электронные таблицы. Термины и понятия Графические техники
Графические техники Божественная пропорция
Божественная пропорция Детектор. Практика невербальной семиотики, частных телодвижений и мимики. Занятие №9
Детектор. Практика невербальной семиотики, частных телодвижений и мимики. Занятие №9 Теория фирмы
Теория фирмы Спор Афины с Посейдоном
Спор Афины с Посейдоном МногомернаяСУБД UMS-FAD
МногомернаяСУБД UMS-FAD Принцип парламентаризма в Германии
Принцип парламентаризма в Германии Трудоустройство несовершеннолетних
Трудоустройство несовершеннолетних 1664472877325__ivhdl (1)
1664472877325__ivhdl (1) Хто може бути експертом?
Хто може бути експертом? Презентация на тему Проводники и изоляторы
Презентация на тему Проводники и изоляторы Анализ учебно-воспитательной работы за 2011-2012 учебный год ГБОУ СОШ «Школа здоровья» №198
Анализ учебно-воспитательной работы за 2011-2012 учебный год ГБОУ СОШ «Школа здоровья» №198 О знаках препинания
О знаках препинания Аптека на грядке: бабушкина капуста
Аптека на грядке: бабушкина капуста творцы фезической науки
творцы фезической науки Путешествие по сказкам Г.Х.Андерсена
Путешествие по сказкам Г.Х.Андерсена Устройство и техническое обслуживание автомобилей классификация грузовых автомобилей
Устройство и техническое обслуживание автомобилей классификация грузовых автомобилей