Перпендикулярность

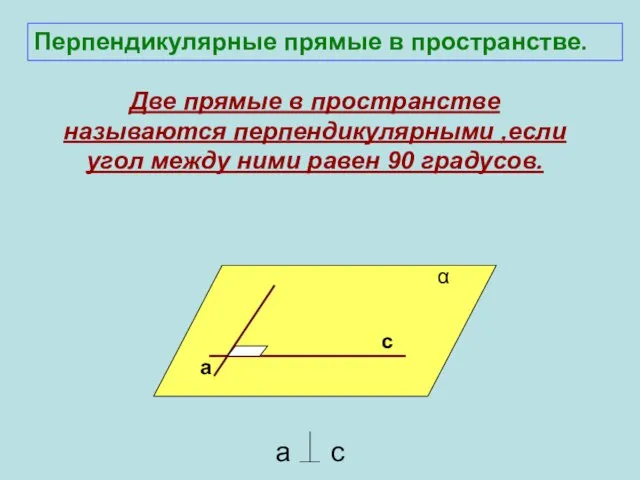
Две прямые в пространстве называются перпендикулярными ,если угол между ними равен 90 градусов.
а с
c
a
α
Перпендикулярные прямые в пространстве.

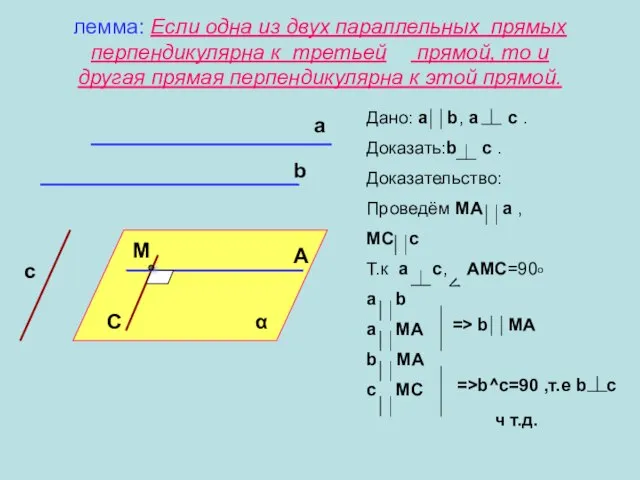
лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
.
М
α
А
С
с
b
a
Дано: а b, a c .
Доказать:b c .
Доказательство:
Проведём МА а ,
МС с
Т.к а с, AMC=90
a b
a MA
b MA
c MC
ч т.д.
о
<
=> b MA
=>b^c=90 ,т.е b c

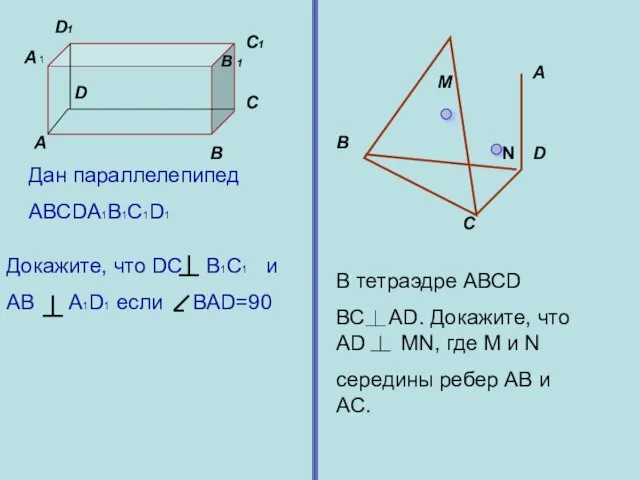
А
В
С
D
А 1
В 1
С1
D1
Докажите, что DC B1C1 и
AB A1D1 если ВАD=90
А
D
В
С
В тетраэдре АВСD
ВС АD. Докажите, что АD MN, где М и N
середины ребер АВ и АС.
М
.
.
N
Дан параллелепипед
АВСDA1B1C1D1

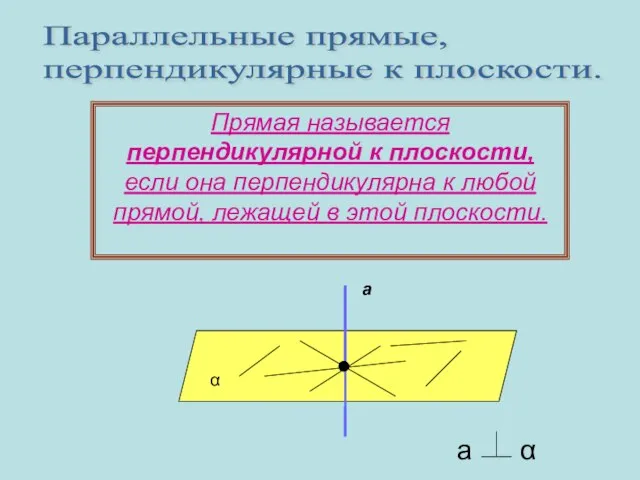
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
а α
Параллельные прямые,
перпендикулярные к плоскости.
а
α

Национальный
Парк Чехии.

Эрмитаж

Парламент
на
Дунае
в Венгрии

Танцующий дом
Падающая башня

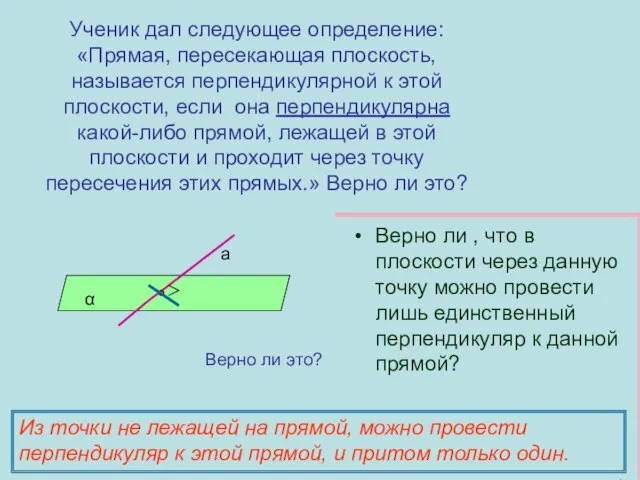
Ученик дал следующее определение:
«Прямая, пересекающая плоскость,
называется перпендикулярной к этой
плоскости, если она перпендикулярна
какой-либо прямой, лежащей в этой
плоскости и проходит через точку пересечения этих прямых.» Верно ли это?
Верно ли , что в плоскости через данную точку можно провести лишь единственный перпендикуляр к данной прямой?
α
а
Из точки не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Верно ли это?

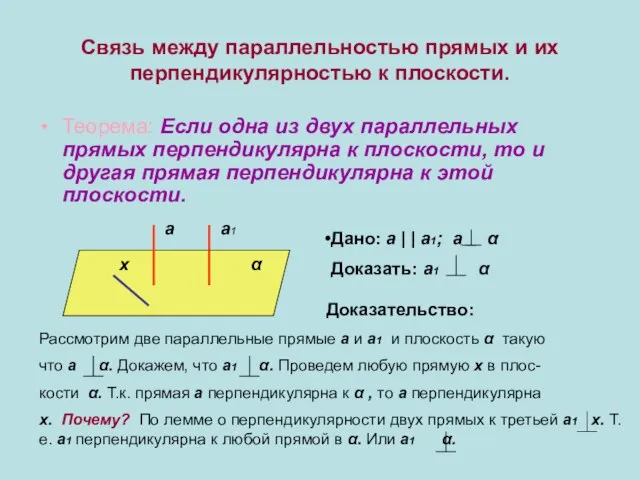
Связь между параллельностью прямых и их перпендикулярностью к плоскости.
Теорема: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
а1
а
α
х
Дано: а | | а1; а α
Доказать: а1 α
Доказательство:
Рассмотрим две параллельные прямые а и а1 и плоскость α такую
что а α. Докажем, что а1 α. Проведем любую прямую х в плос-
кости α. Т.к. прямая а перпендикулярна к α , то а перпендикулярна
х. Почему? По лемме о перпендикулярности двух прямых к третьей а1 х. Т.е. а1 перпендикулярна к любой прямой в α. Или а1 α.