Содержание
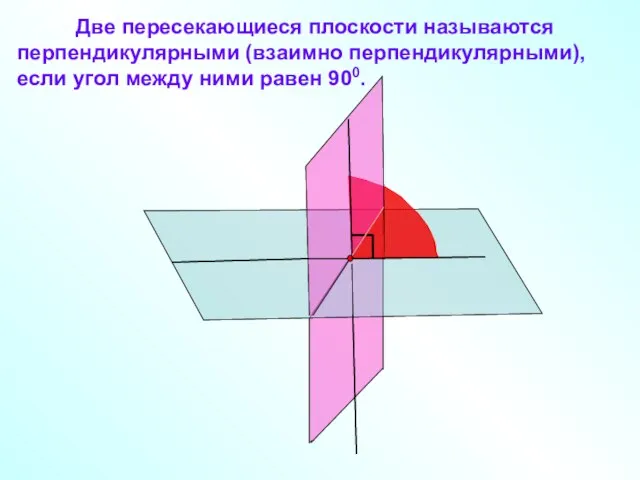
- 2. Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 900.
- 3. Примером взаимно перпендикулярных плоскостей служат плоскости стены и пола комнаты, плоскости стены и потолка.
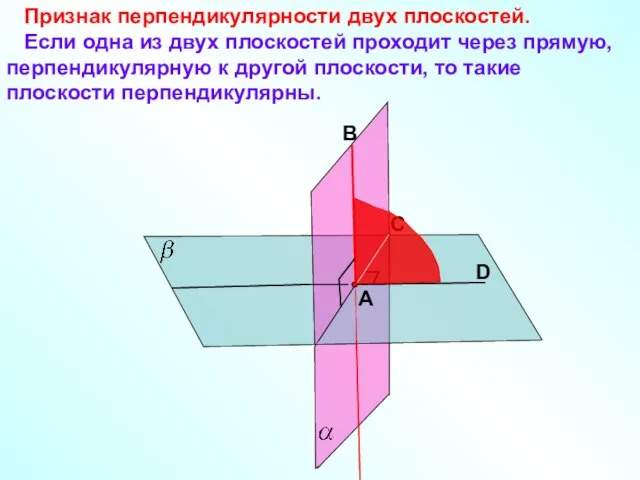
- 4. Признак перпендикулярности двух плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости,
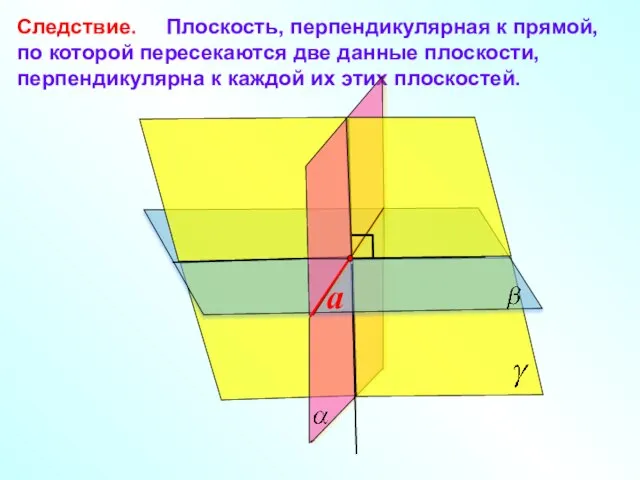
- 5. Следствие. Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой их этих
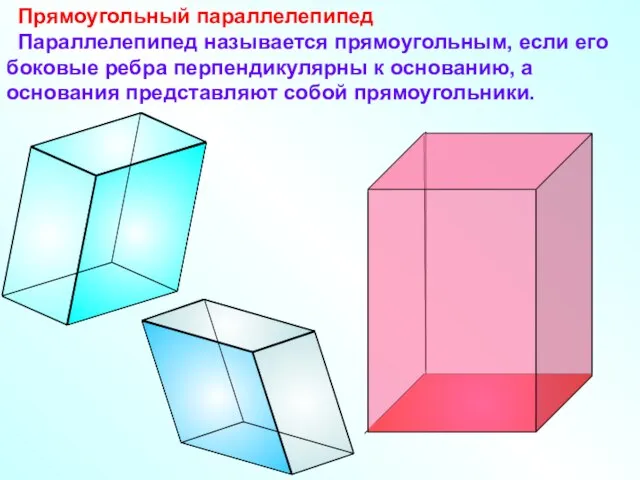
- 6. Прямоугольный параллелепипед Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой
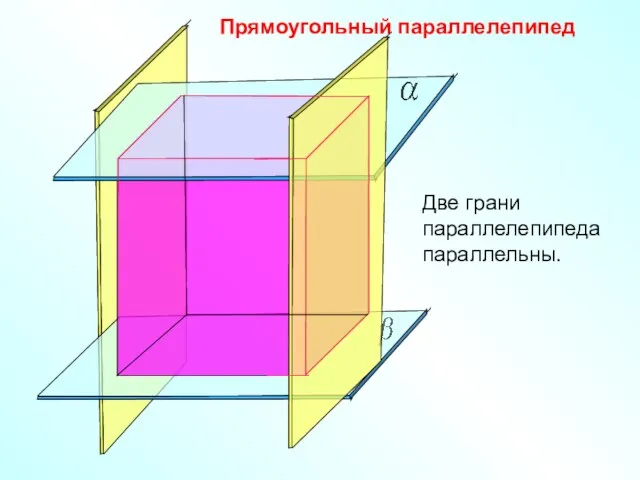
- 7. Прямоугольный параллелепипед Две грани параллелепипеда параллельны.
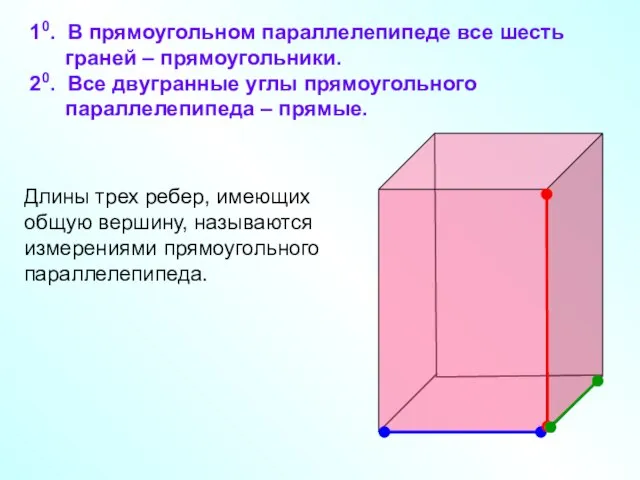
- 8. 10. В прямоугольном параллелепипеде все шесть граней – прямоугольники. 20. Все двугранные углы прямоугольного параллелепипеда –
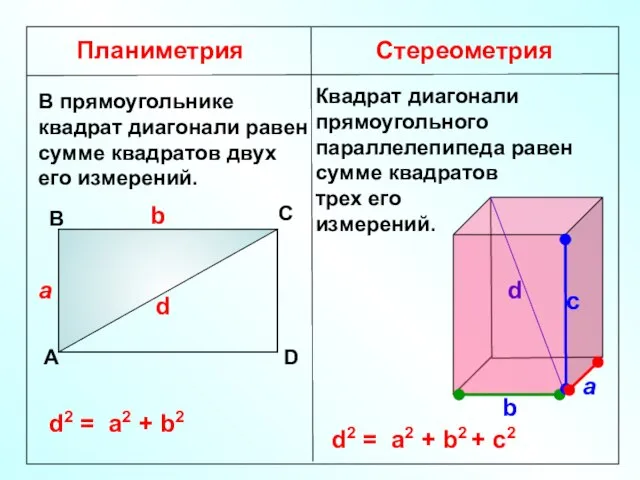
- 9. Планиметрия Стереометрия В прямоугольнике квадрат диагонали равен сумме квадратов двух его измерений. А В С D
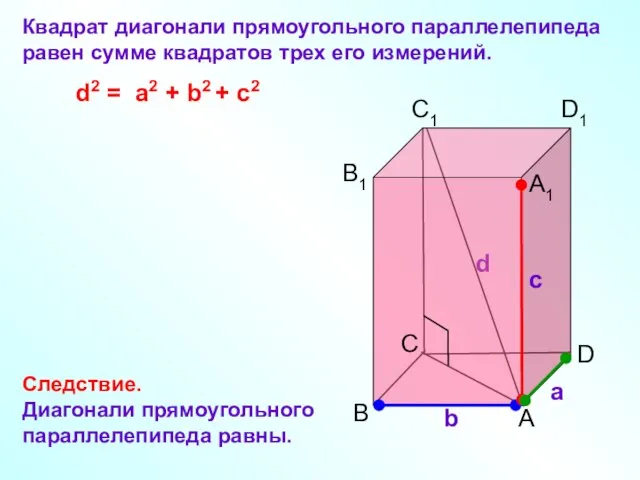
- 10. C а b с B A D B1 C1 D1 A1 Квадрат диагонали прямоугольного параллелепипеда равен
- 12. Скачать презентацию

 Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году
Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году Тунгусский метеорит
Тунгусский метеорит Отечественная война 1812 года.
Отечественная война 1812 года. Общие положения о праве. Тема 2
Общие положения о праве. Тема 2 ПОРЯДОК ПРОВЕДЕНИЯ ЕГЭ В 2010 ГОДУ
ПОРЯДОК ПРОВЕДЕНИЯ ЕГЭ В 2010 ГОДУ Физика твердого тела
Физика твердого тела Влияние физкультуры и спорта на формирование личности и характера
Влияние физкультуры и спорта на формирование личности и характера Детские писатели
Детские писатели ДОРОЖНЫЕ ЗНАКИ
ДОРОЖНЫЕ ЗНАКИ Тема: «Тайны древних пирамид» Маркова Марина Валерьевна 2009 – 2010 учебный год
Тема: «Тайны древних пирамид» Маркова Марина Валерьевна 2009 – 2010 учебный год Ветер перемен, или современный урок в зеркале стандартов нового поколения.
Ветер перемен, или современный урок в зеркале стандартов нового поколения. Сходство и различие фразеологизмов и пословиц
Сходство и различие фразеологизмов и пословиц Виктор Драгунский«Друг детства»
Виктор Драгунский«Друг детства» Здоровый рост и развитие с Royal Canin
Здоровый рост и развитие с Royal Canin Басқа елдердең сүт тағамдары дайындала ма
Басқа елдердең сүт тағамдары дайындала ма Конкурс знатоков
Конкурс знатоков Понятие о маркетинговой среде
Понятие о маркетинговой среде Искусство на улицах моего города
Искусство на улицах моего города Что не так?
Что не так? Техника мраморирования в современном дизайне
Техника мраморирования в современном дизайне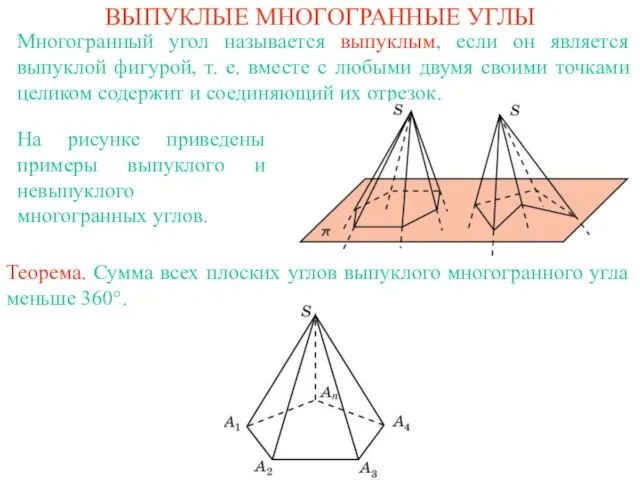 Выпуклые многогранные углы
Выпуклые многогранные углы Кулинарная азбука
Кулинарная азбука Причастие и его особенности
Причастие и его особенности Презентация на тему Дискретные и непрерывные сигналы. Носители информации
Презентация на тему Дискретные и непрерывные сигналы. Носители информации Убойный арсенал настоящей леди. Косметичка из масс-маркета
Убойный арсенал настоящей леди. Косметичка из масс-маркета Evolyutsia_upravlencheskoy_mysli
Evolyutsia_upravlencheskoy_mysli Бетон и железобетон
Бетон и железобетон Простейший ремонт сантехнического оборудования
Простейший ремонт сантехнического оборудования