Перпендикулярность прямых и плоскостей (10 класс)

Определение. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Теорема 3.1 Если две пересекающие
прямые параллельны соответственно
двум перпендикулярным прямым,
то они тоже перпендикулярны.
a
b
a1
b1
C
C1
A
A1
B
B1

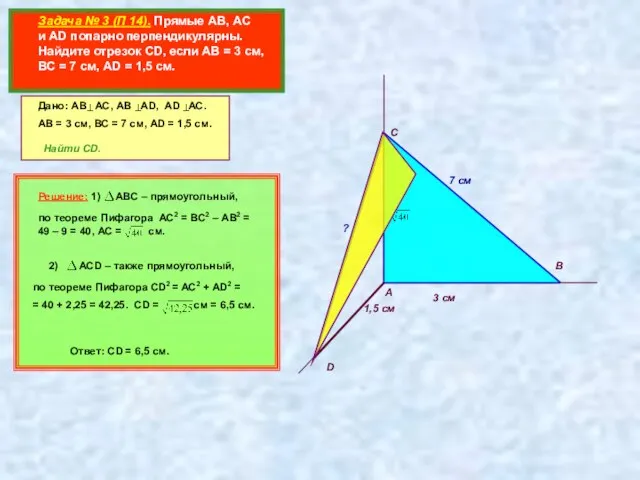
Задача № 3 (П 14). Прямые АВ, АС и AD попарно перпендикулярны. Найдите отрезок CD, если АВ = 3 см, ВС = 7 см, АD = 1,5 см.
А
В
С
D
Дано: АВ АС, АВ АD, AD AC.
АВ = 3 см, ВС = 7 см, АD = 1,5 см.
3 см
7 см
1,5 см
Найти CD.
?
Решение: 1) АВС – прямоугольный,
по теореме Пифагора АС2 = ВС2 – АВ2 = 49 – 9 = 40, АС = см.
2) АСD – также прямоугольный,
по теореме Пифагора СD2 = AC2 + AD2 =
= 40 + 2,25 = 42,25. CD = cм = 6,5 см.
Ответ: CD = 6,5 см.

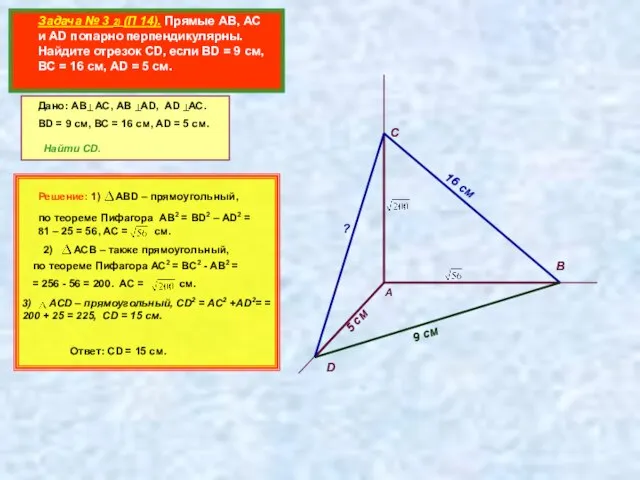
Задача № 3 2) (П 14). Прямые АВ, АС и AD попарно перпендикулярны. Найдите отрезок CD, если ВD = 9 см, ВС = 16 см, АD = 5 см.
А
В
С
D
Дано: АВ АС, АВ АD, AD AC.
BD = 9 см, ВС = 16 см, АD = 5 см.
16 см
5 см
Найти CD.
?
Решение: 1) АВD – прямоугольный,
по теореме Пифагора АB2 = ВD2 – АD2 = 81 – 25 = 56, АС = см.
2) АСB – также прямоугольный,
по теореме Пифагора AC2 = BC2 - AB2 =
= 256 - 56 = 200. AC = cм.
Ответ: CD = 15 см.
9 см
3) ACD – прямоугольный, CD2 = AC2 +AD2= = 200 + 25 = 225, CD = 15 см.

Перпендикулярность прямой и плоскости.
Определение. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения данной прямой и плоскости

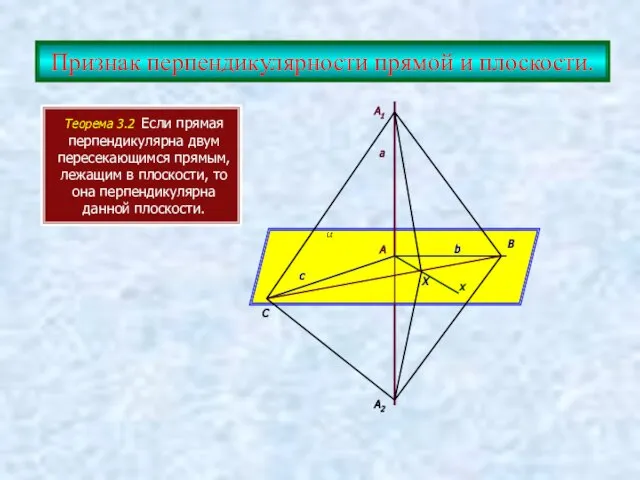
Признак перпендикулярности прямой и плоскости.
Теорема 3.2 Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.
a
b
c
x
C
X
B
A
A1
A2

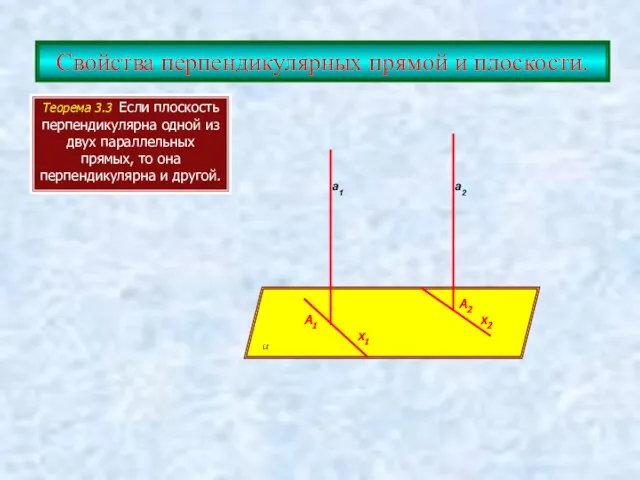
Свойства перпендикулярных прямой и плоскости.
Теорема 3.3 Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
a1
a2
A1
A2
x2
x1

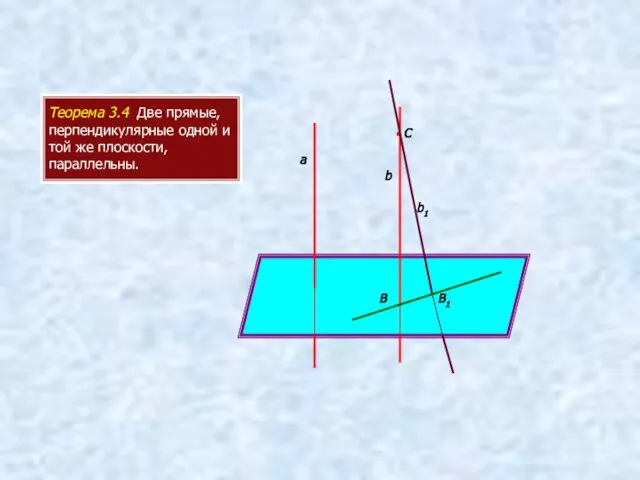
Теорема 3.4 Две прямые, перпендикулярные одной и той же плоскости, параллельны.
а
b
• С
b1
В
В1

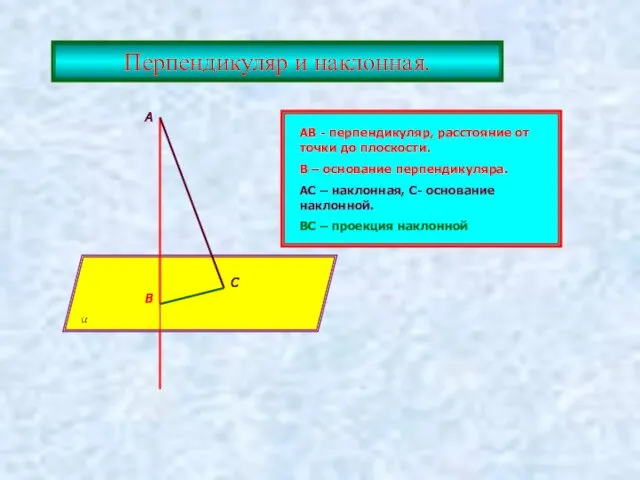
Перпендикуляр и наклонная.
А
В
С
АВ - перпендикуляр, расстояние от точки до плоскости.
В – основание перпендикуляра.
АС – наклонная, С- основание наклонной.
ВС – проекция наклонной

Задача Из точки к плоскости проведены две наклонные, равные 15 см и 20 см. Разность проекций этих наклонных равна 7 см. Найдите проекции наклонных.
А
В
20 см
С
15 см
7 см
О
Дано: АВ и АС – наклонные к плоскости
АО , АВ = 20 см, АС = 15 см, ВС = 7 см.
Найти: ВО и СО.
Решение:
1) Найдём площадь АВС по формуле Герона: .
p = (a+b+c)/2 = (20+15+7)/2 = 21 см.
= 7·6 = 42 см2.
2)
, АО = 2·42/7 = 84/7 = 12 см.
12 см
АOС – прямоугольный, по теореме Пифагора ОС2 = АС2 – АО2 = 225 – 144 = 81,
ОС = 9 см.
4) ОВ = ВС + ОС = 7 + 9 = 16 см.
Ответ: 9 см и 16 см.
9 см

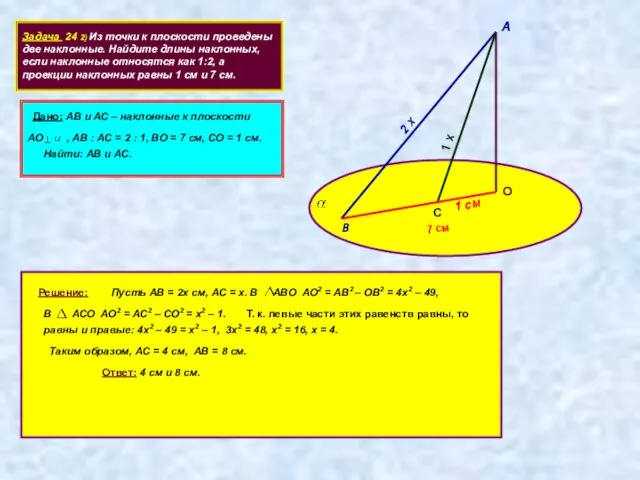
Задача 24 2) Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если наклонные относятся как 1:2, а проекции наклонных равны 1 см и 7 см.
А
В
2 х
С
1 х
7 см
О
Дано: АВ и АС – наклонные к плоскости
АО , АВ : АС = 2 : 1, ВО = 7 см, СО = 1 см.
Найти: АВ и АС.
Решение:
Ответ: 4 см и 8 см.
1 см
Пусть АВ = 2х см, АС = х. В АВО АО2 = АВ2 – ОВ2 = 4х2 – 49,
В АСО АО2 = АС2 – СО2 = х2 – 1.
Т. к. левые части этих равенств равны, то
равны и правые: 4х2 – 49 = х2 – 1, 3х2 = 48, х2 = 16, х = 4.
Таким образом, АС = 4 см, АВ = 8 см.

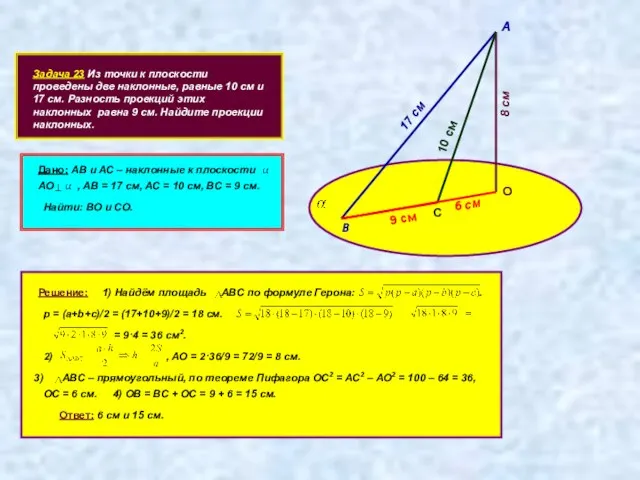
Задача 23 Из точки к плоскости проведены две наклонные, равные 10 см и 17 см. Разность проекций этих наклонных равна 9 см. Найдите проекции наклонных.
А
В
17 см
С
10 см
9 см
О
Дано: АВ и АС – наклонные к плоскости
АО , АВ = 17 см, АС = 10 см, ВС = 9 см.
Найти: ВО и СО.
Решение:
1) Найдём площадь АВС по формуле Герона: .
p = (a+b+c)/2 = (17+10+9)/2 = 18 см.
= 9·4 = 36 см2.
2)
, АО = 2·36/9 = 72/9 = 8 см.
8 см
АВС – прямоугольный, по теореме Пифагора ОС2 = АС2 – АО2 = 100 – 64 = 36,
ОС = 6 см.
4) ОВ = ВС + ОС = 9 + 6 = 15 см.
Ответ: 6 см и 15 см.
6 см

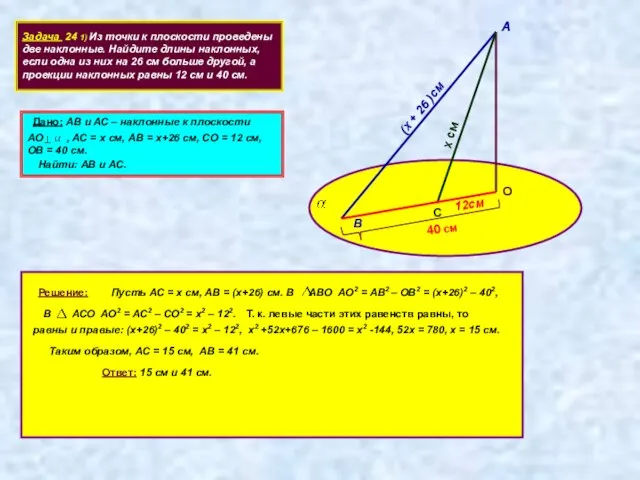
Задача 24 1) Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если одна из них на 26 см больше другой, а проекции наклонных равны 12 см и 40 см.
А
В
(х + 26 )см
С
х см
40 см
О
Дано: АВ и АС – наклонные к плоскости
АО , АС = х см, АВ = х+26 см, СО = 12 см, ОВ = 40 см.
Найти: АВ и АС.
Решение:
Ответ: 15 см и 41 см.
12см
Пусть АС = х см, АВ = (х+26) см. В АВО АО2 = АВ2 – ОВ2 = (х+26)2 – 402,
В АСО АО2 = АС2 – СО2 = х2 – 122.
Т. к. левые части этих равенств равны, то
равны и правые: (х+26)2 – 402 = х2 – 122, х2 +52х+676 – 1600 = х2 -144, 52х = 780, х = 15 см.
Таким образом, АС = 15 см, АВ = 41 см.

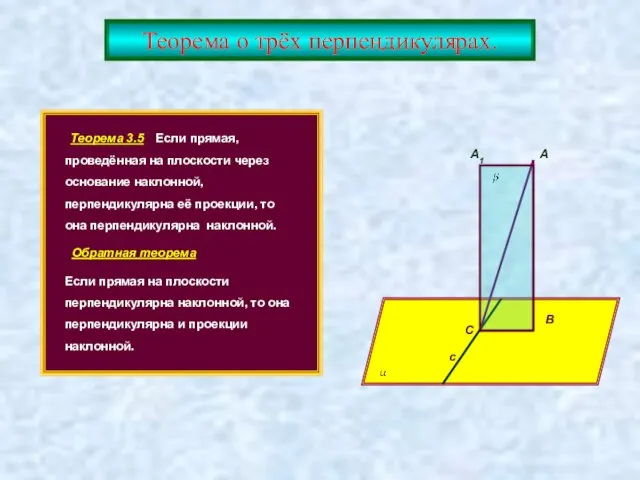
Теорема о трёх перпендикулярах.
Теорема 3.5 Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна наклонной.
Обратная теорема
Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
А
В
С
А1
с

Задача № 48. Из вершины равностороннего треугольника АВС восставлен перпендикуляр AD к плоскости треугольника. Найдите расстояние от точки D до стороны ВС, если AD = 13 см, ВС = 6 см.
А
В
С
D
F
6 см
6 см
6 см
13 см
Дано: АВС – равносторонний, АВ=ВС=АС= 6 см, АD (АВС), АD=13 см.
Найдите: (D; BC).
Решение: Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из данной точки до прямой. Поэтому, из точки D опустим перпендикуляр DF на прямую ВС.
По теореме о трёх перпендикулярах AF BC,
т.к. треугольник АВС- равносторонний, то АF –медиана, т.е. BF=FC= 3 см.
АFC – прямоугольный. По теореме Пифагора AF2 = AC2 – CF2 = 36 – 9 = 27, AF = см.
ADF – прямоугольный, DF2 = AD2 + AF2 = 169 + 27 = 196, следовательно DF = 14 см.
Ответ: 14 см.

Задача . Стороны треугольника 15 см, 26 см и 37 см. Через вершину среднего по величине угла проведён перпендикуляр в его плоскости, равный 9 см. Найдите расстояние от концов этого перпендикуляра до противоположной стороны.
А
В
С
D
15 см
37 см
26 см
9 см
Решение: Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из данной точки до прямой. Поэтому, из точки В опустим перпендикуляр ВF на прямую ВС.
F
По теореме о трёх перпендикулярах DF AC.
BF найдём из треугольника АВС.
Найдём площадь треугольника АВС по формуле Герона.
p = (a+b+c)/2 = (15+26+37)/2 = 39,
S =
= 13·3·4 = 156 (см2).
S= AC·BF,
BF = 2·S/AC= 2·156 / 26 = 12 см.
12 см
Треугольник DFB – прямоугольный.
По теореме Пифагора DF2 = DB2 + BF2 ,
DF2 = 81 + 144 = 225, DF = 15 см.
Ответ: 12 см и 15 см.

Задание на дом: П. 19,
Задача . Из вершины треугольника АВС восставлен перпендикуляр ВD к
плоскости треугольника. Найдите
расстояние от точки D до стороны АС,
если ВD = 9 см, АВ = 15 см, ВС = 20 см, АС = 7 см.

Задача . Из вершины треугольника АВС восставлен перпендикуляр ВD к плоскости треугольника. Найдите расстояние от точки D до стороны АС, если ВD = 9 см, АВ = 15 см, ВС = 20 см, АС = 7 см.
А
В
С
D
15 см
20 см
7 см
9 см
Решение: Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из данной точки до прямой. Поэтому, из точки D опустим перпендикуляр DF на прямую АС.
F
По теореме о трёх перпендикулярах BF AC.
BF найдём из треугольника АВС.
Вычислим площадь треугольника АВС по формуле Герона.
p = (a+b+c)/2 = (15+20+7)/2 = 21,
S =
=
=
=
7·6 = 42 (см2).
S= AC·BF,
BF = 2·S/AC= 2·42 / 7 = 12 см.
12 см
Треугольник DFB – прямоугольный.
По теореме Пифагора DF2 = DB2 + BF2 ,
DF 2 = 81 + 144 = 225, DF = 15 см.
Ответ: 15 см.
15 см

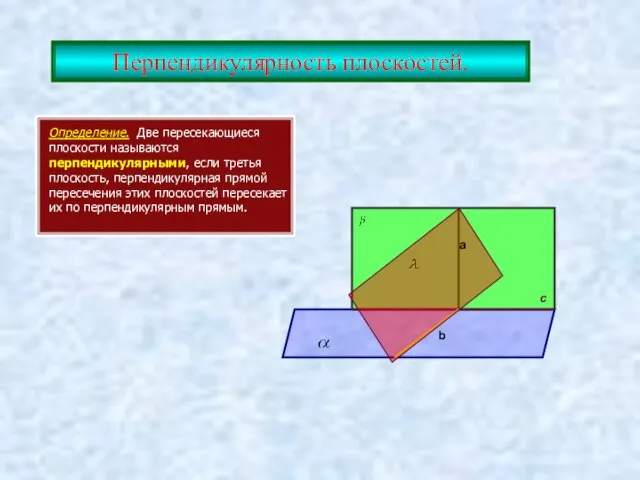
Перпендикулярность плоскостей.
Определение. Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей пересекает их по перпендикулярным прямым.
с
a
b

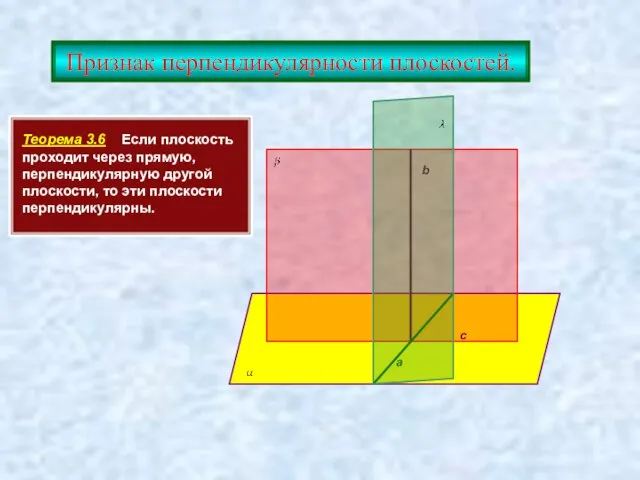
Признак перпендикулярности плоскостей.
Теорема 3.6 Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
b
c
a

Задача № 59 1) Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ, если: АС = 6 м, ВD = 7 м, СD = 6 м.
•
А
•
В
С
D
Дано: , А∈ , В∈ , АС CD, BD CD
АС = 6 м, ВD = 7 м, СD = 6 м.
Найти: АВ.
6 м
7 м
6 м
?
Решение: BCD – прямоугольный,
900
по теореме Пифагора ВС2 = СD2 + BD2,
ВС2 = 36 +49 = 85, ВС = м.
АВС – прямоугольный,
900
по теореме Пифагора АВ2 = АС2 + ВС2,
АВ2 = 36 + 85 = 121, АВ = 11 м.
Ответ : 11 м.

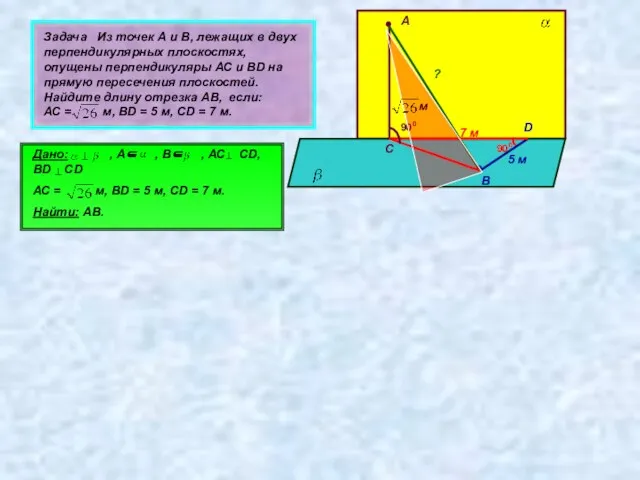
Задача Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ, если: АС = м, ВD = 5 м, СD = 7 м.
•
А
•
В
С
D
Дано: , А∈ , В∈ , АС CD, BD CD
АС = м, ВD = 5 м, СD = 7 м.
Найти: АВ.
м
5 м
7 м
?
900
900

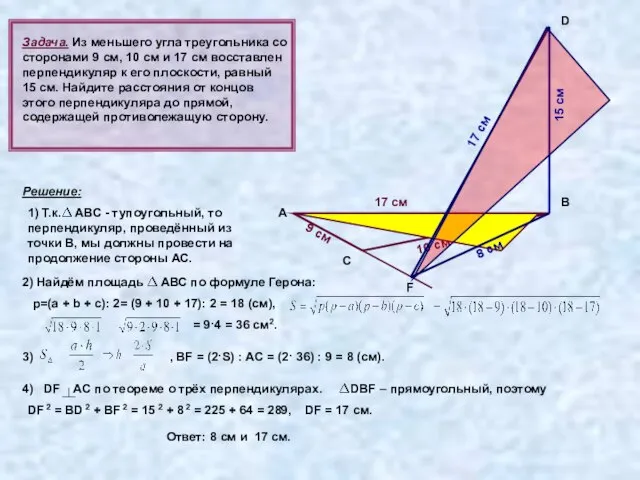
Задача. Из меньшего угла треугольника со сторонами 9 см, 10 см и 17 см восставлен перпендикуляр к его плоскости, равный 15 см. Найдите расстояния от концов этого перпендикуляра до прямой, содержащей противолежащую сторону.
А
В
С
D
9 см
10 см
17 см
Решение:
1) Т.к. АВС - тупоугольный, то перпендикуляр, проведённый из точки В, мы должны провести на продолжение стороны АС.
F
2) Найдём площадь АВС по формуле Герона:
p=(a + b + c): 2= (9 + 10 + 17): 2 = 18 (см),
= 9·4 = 36 см2.
3)
, ВF = (2·S) : АС = (2· 36) : 9 = 8 (см).
4)
DF AC по теореме о трёх перпендикулярах.
DBF – прямоугольный, поэтому
DF 2 = BD 2 + BF 2 = 15 2 + 8 2 = 225 + 64 = 289,
DF = 17 см.
Ответ: 8 см и 17 см.
8 см
15 см
17 см

Задание на дом: П 20,
задачи № № 25, 59 3),

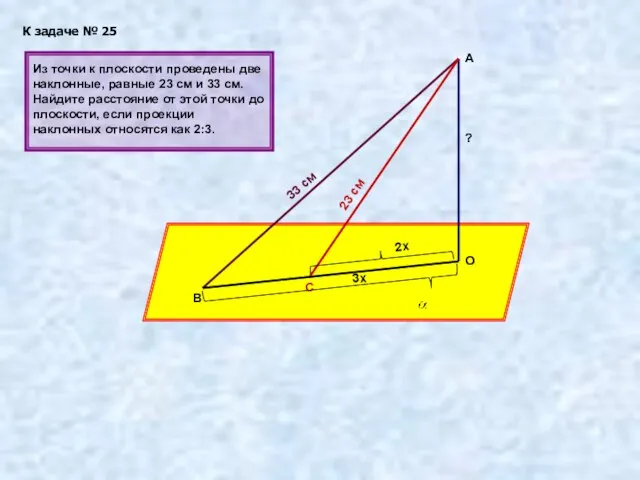
К задаче № 25
А
В
О
С
33 см
23 см
3х
2х
Из точки к плоскости проведены две наклонные, равные 23 см и 33 см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3.
?