Векторы в пространстве и не только

Цели урока
Знать: определение вектора в пространстве и связанные с ним понятия; равенство векторов.
Уметь: решать задачи по данной теме.

Физические величины
Скорость
Ускорение а
Перемещение s
Сила F
v

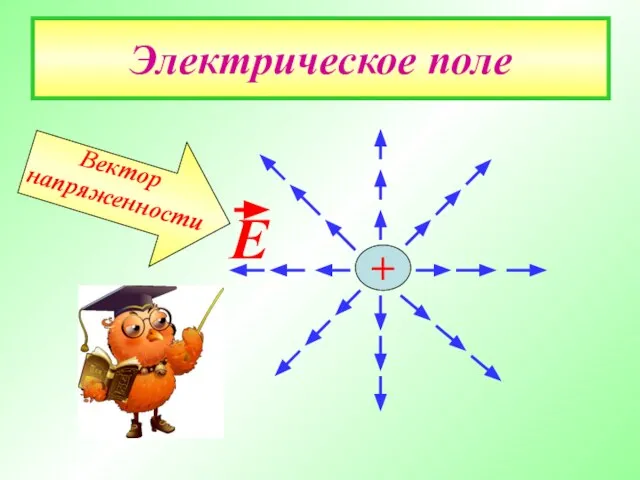
Электрическое поле
Е

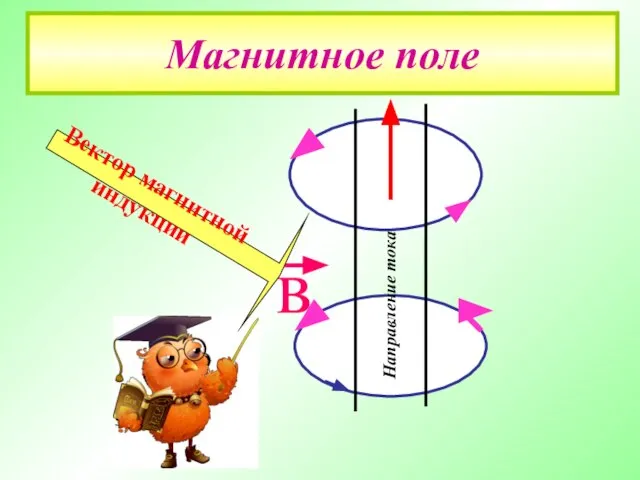
Магнитное поле
Направление тока
в

Понятие вектора появилось в 19 веке в работах математиков
Г. Грассмана У. Гамильтона

Современная символика для обозначения вектора r была введена в 1853 году французским математиком О. Коши.

Задание
Записать все термины по теме «Векторы на плоскости».
Вектор
Нулевой вектор
Длина вектора
Коллинеарные векторы
Сонаправленные векторы
Противоположно направленные векторы
Равенство векторов

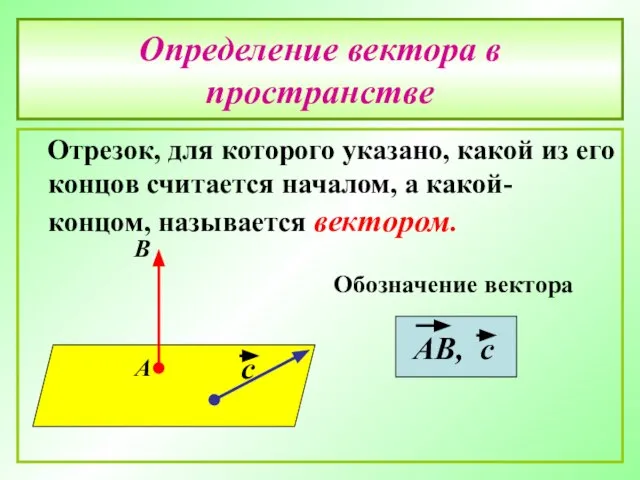
Определение вектора в пространстве
Отрезок, для которого указано, какой из его концов считается началом, а какой- концом, называется вектором.

Т
Любая точка пространства также
может рассматриваться как вектор. Такой вектор называется
нулевым.

Длина ненулевого вектора
Длиной вектора АВ называется длина отрезка АВ.
Длина вектора АВ (вектора а) обозначается так:
АВ , а
Длина нулевого вектора считается равной нулю:
0
= 0

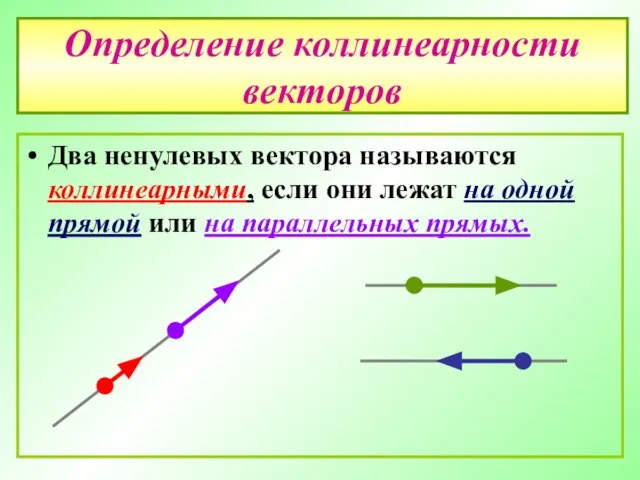
Определение коллинеарности векторов
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

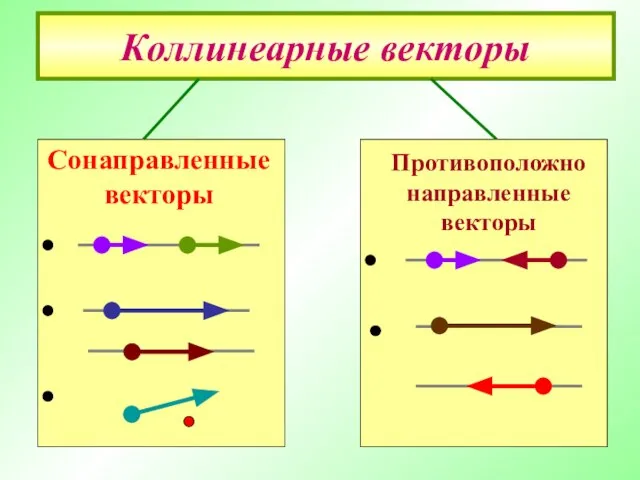
Коллинеарные векторы
Противоположно направленные векторы
Сонаправленные векторы

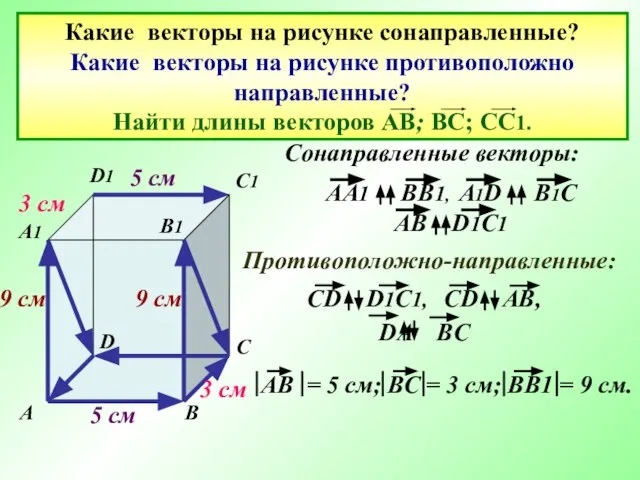
Какие векторы на рисунке сонаправленные?
Какие векторы на рисунке противоположно направленные?
Найти длины векторов АВ; ВС; СС1.
A
B
C
D
В1
D1
A1
C1
Сонаправленные векторы:
Противоположно-направленные:
5 см
3 см
9 см
5 см
3 см
9 см

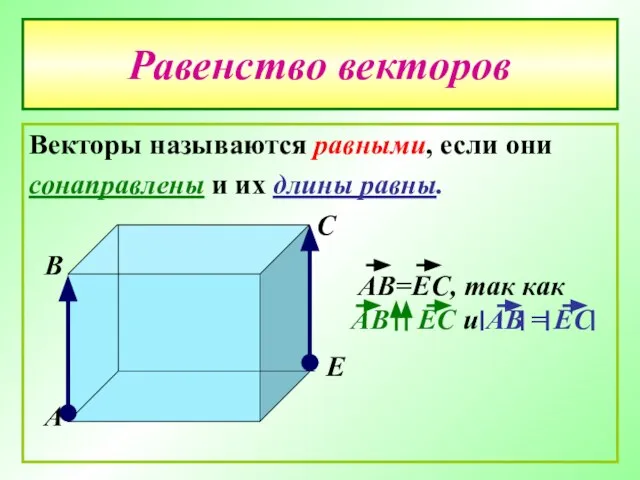
Равенство векторов
Векторы называются равными, если они
сонаправлены и их длины равны.
А
В
С
Е

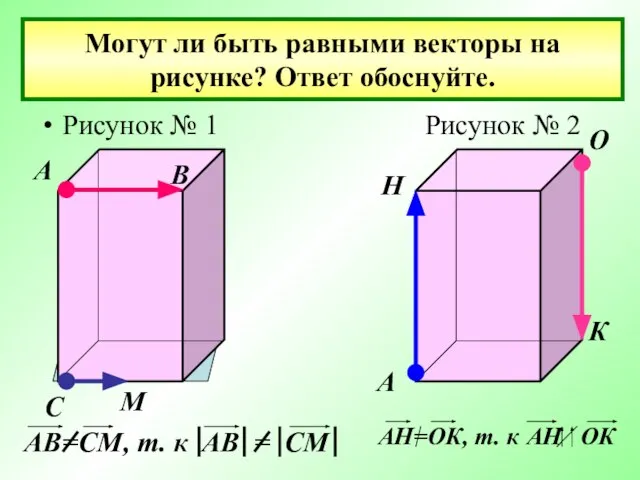
Могут ли быть равными векторы на рисунке? Ответ обоснуйте.
Рисунок № 1 Рисунок № 2
А
В
С
М
А
Н
О

Доказать, что от любой точки пространства можно отложить вектор, равный данному, и притом только один
Дано: а, М.
Доказать: в = а, М в, единственный.
Доказательство:
Проведем через вектор а и точку
М плоскость.
М
К

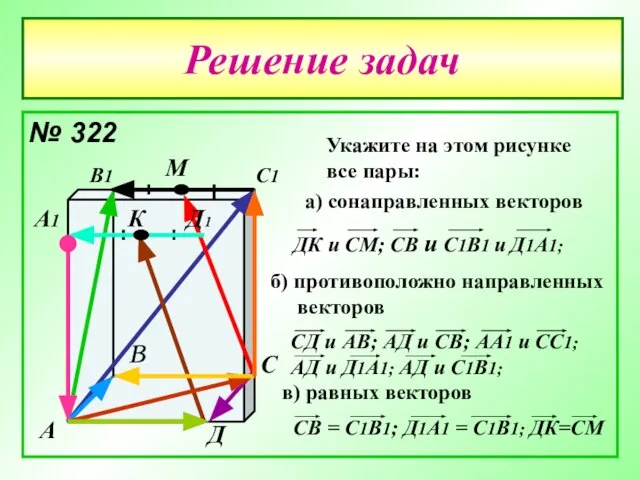
Решение задач
№ 322
А
В
С
Д
А1
В1
С1
Д1
М
К
Укажите на этом рисунке
все пары:
а) сонаправленных векторов
б) противоположно направленных векторов
в) равных векторов

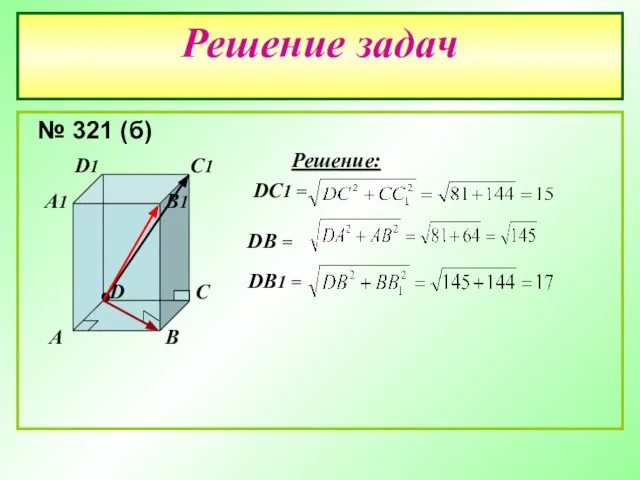
Решение задач
№ 321 (б)
A
B
C
D
A1
B1
C1
D1
Решение:
DC1 =
DB =
DB1 =

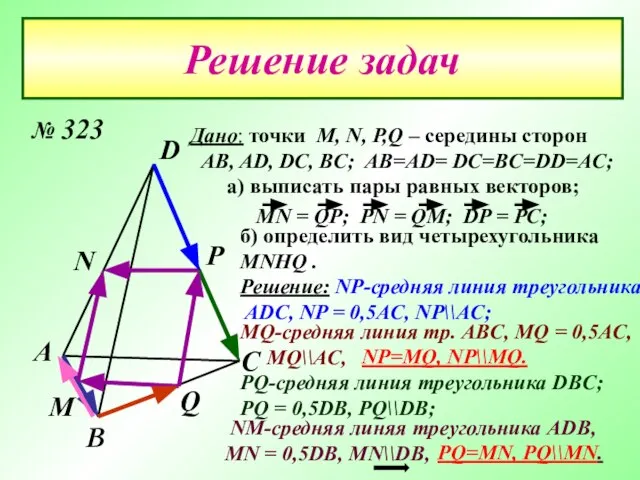
Решение задач
А
D
С
В
М
Р
N
Q
Дано: точки М, N, P,Q – середины сторон
AB, AD, DC, BC; AB=AD= DC=BC=DD=AC;
а) выписать пары равных векторов;
б) определить вид четырехугольника
MNHQ .
NM-средняя линяя треугольника ADB,
MN = 0,5DB, MN\\DB,
MQ-средняя линия тр. ABC, MQ = 0,5AC,
MQ\\AC,
Решение: NP-средняя линия треугольника
ADC, NP = 0,5AC, NP\\AC;
NP=MQ, NP\\MQ.
PQ-средняя линия треугольника DВC;
PQ = 0,5DB, PQ\\DB;
PQ=MN, PQ\\MN.
№ 323

По условию все ребра тетраэдра равны, то он правильный и скрещивающиеся ребра в нем перпендикулярны.
DB перпендикулярно АС .
NP=MQ=PQ=MN
NP\\MQ
MN\\PQ
MNPQ-
квадрат

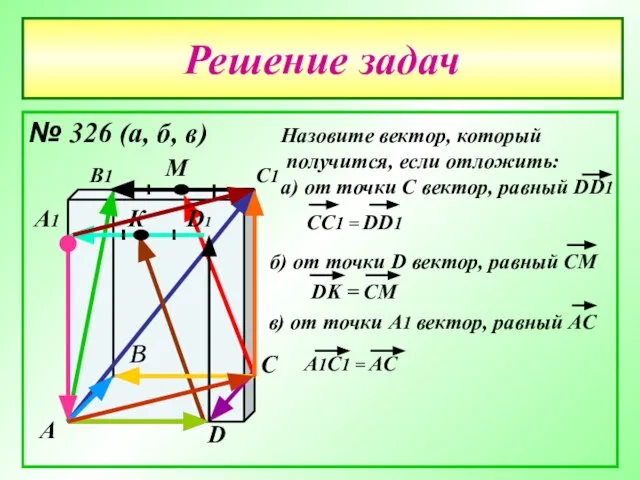
Решение задач
№ 326 (а, б, в)
А
В
С
D
А1
В1
С1
D1
М
К

Самостоятельная работа
Дан тетраэдр МАВС, угол АСВ прямой. Точки К и Р середины сторон МВ и МС, АС = 9 см и ВА = 15 см. Найти КМ .
Решение:
М
А
В
С
К
М
Треугольник АВС, угол АСВ- прямой.
9
15
По теореме Пифагора

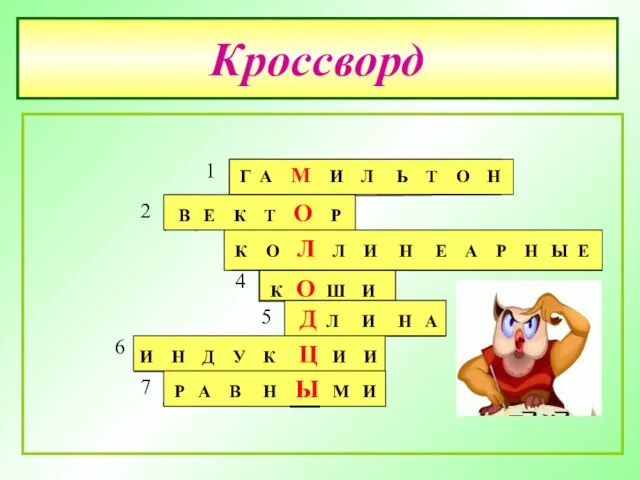
Кроссворд
Г А М И Л Ь Т О Н
В Е К Т О Р
К О Л Л И Н Е А Р Н Ы Е
К О Ш И
Д Л И Н А
И Н Д У К Ц И И
Р А В Н Ы М И
1
2
4
5
6
7

Домашнее задание
Стр. 84 – 85
№ 320, 321(а), 325.

Перемена