Презентация на тему Перпендикулярные прямые в пространстве

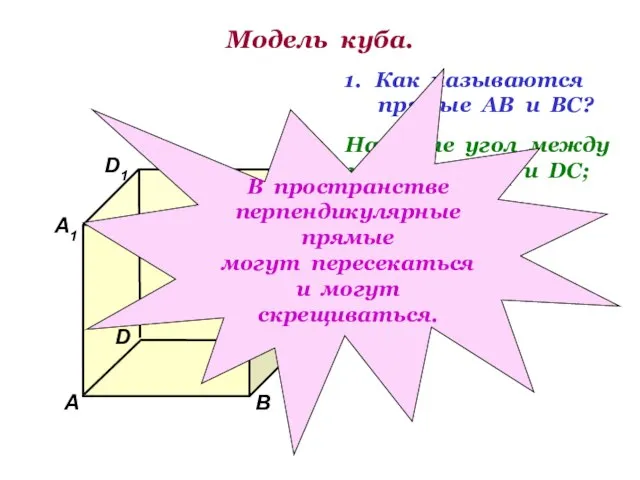
Модель куба.
D1
В
А1
А
D
С1
С
В1
Как называются
прямые АВ и ВС?
Найдите угол между
прямыми АА1 и DC;
ВВ1 и АD.
В пространстве
перпендикулярные прямые
могут пересекаться
и могут скрещиваться.

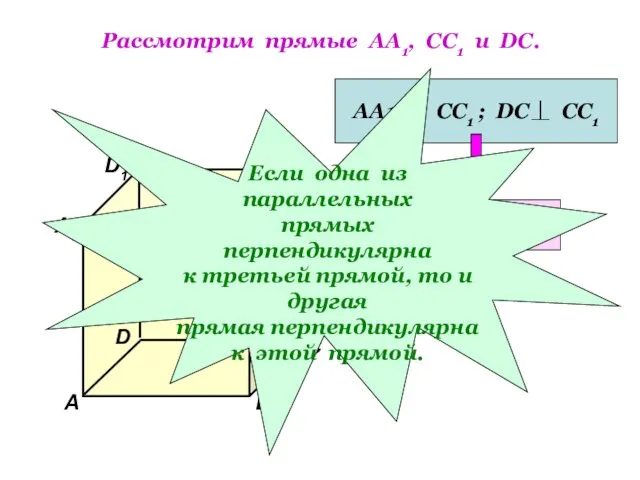
Рассмотрим прямые АА1, СС1 и DC.
D1
В
А1
А
D
С1
С
В1
АА1 ‌|| ‌ СС1 ; DC СС1
АА1 DC
Если одна из параллельных
прямых перпендикулярна
к третьей прямой, то и другая
прямая перпендикулярна
к этой прямой.

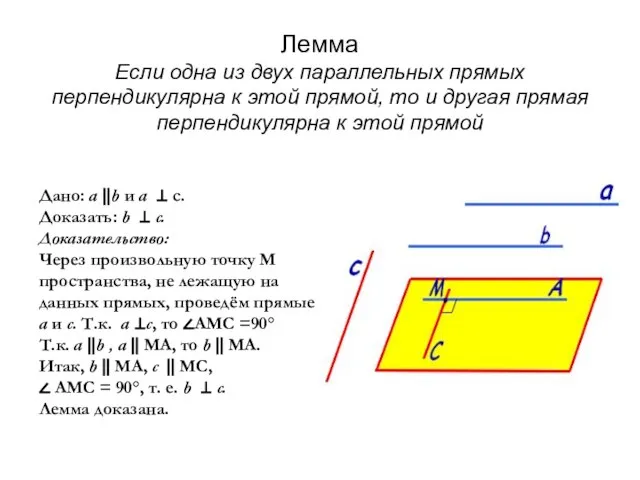
Лемма
Если одна из двух параллельных прямых перпендикулярна к этой прямой, то и другая прямая перпендикулярна к этой прямой
Дано: а ⃦b и а ⊥ с.
Доказать: b ⊥ c.
Доказательство:
Через произвольную точку М пространства, не лежащую на данных прямых, проведём прямые а и с. Т.к. а ⊥с, то ∠АМС =90°
Т.к. а ⃦b , а ⃦ МА, то b ⃦ МА.
Итак, b ⃦ МА, с ⃦ МС,
∠ АМС = 90°, т. е. b ⊥ c.
Лемма доказана.

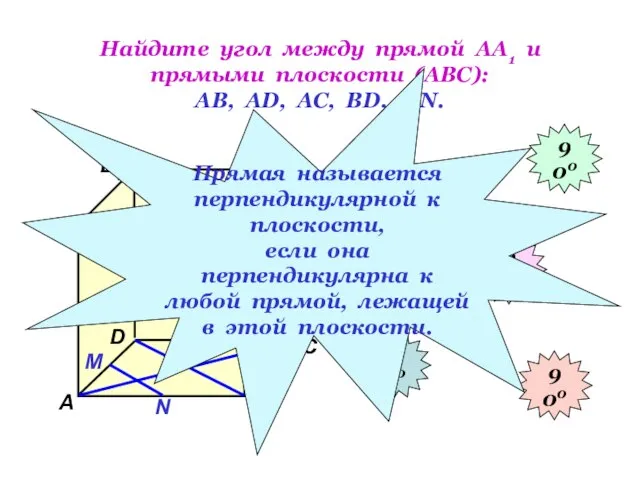
Найдите угол между прямой АА1 и прямыми плоскости (АВС):
АВ, АD, АС, ВD, МN.
D1
В
А1
А
D
С1
С
В1
N
М
900
900
900
900
900
Прямая называется
перпендикулярной к плоскости,
если она перпендикулярна к
любой прямой, лежащей
в этой плоскости.

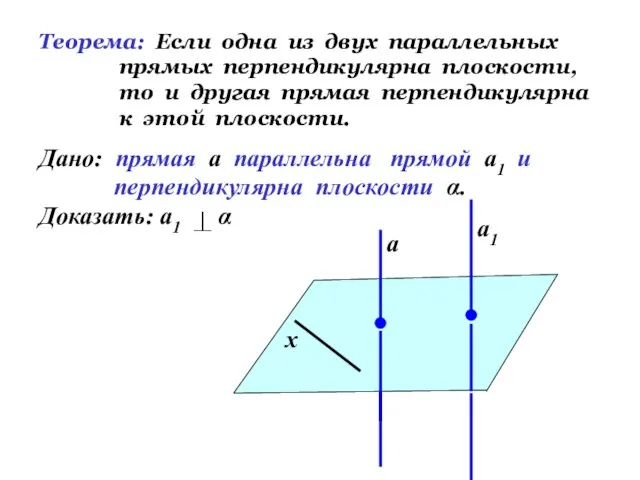
Теорема: Если одна из двух параллельных прямых перпендикулярна плоскости,
то и другая прямая перпендикулярна к этой плоскости.
Дано: прямая а параллельна прямой а1 и
перпендикулярна плоскости α.
Доказать: а1 α
а
а1
х

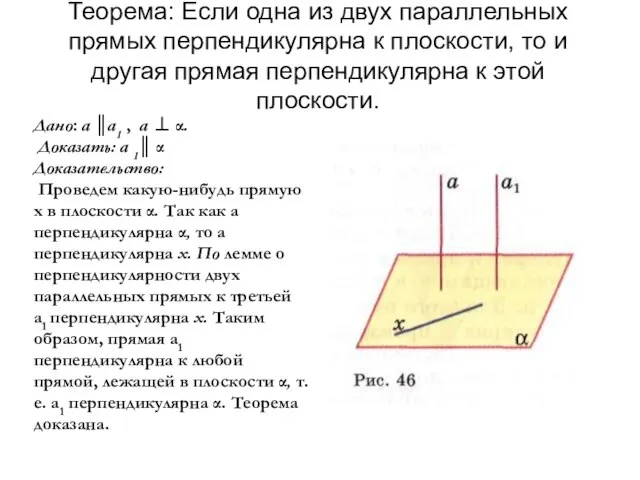
Теорема: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Дано: а ║а1 , а ⊥ α.
Доказать: а 1║ α
Доказательство:
Проведем какую-нибудь прямую х в плоскости α. Так как а перпендикулярна α, то а перпендикулярна х. По лемме о перпендикулярности двух параллельных прямых к третьей а1 перпендикулярна х. Таким образом, прямая а1 перпендикулярна к любой прямой, лежащей в плоскости α, т.е. а1 перпендикулярна α. Теорема доказана.

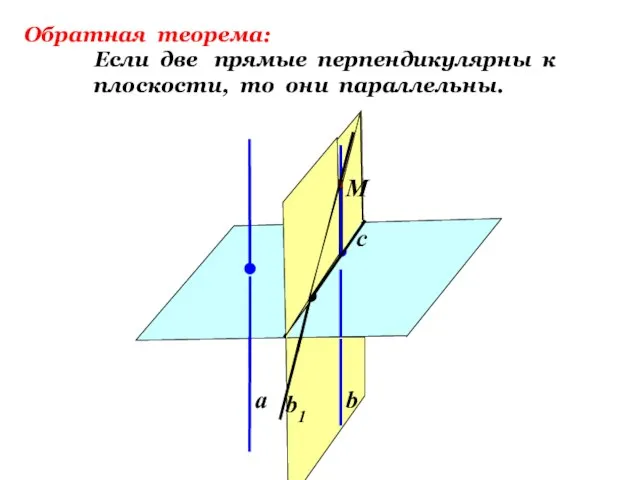
а
b
b1
Обратная теорема:
Если две прямые перпендикулярны к
плоскости, то они параллельны.
M
c

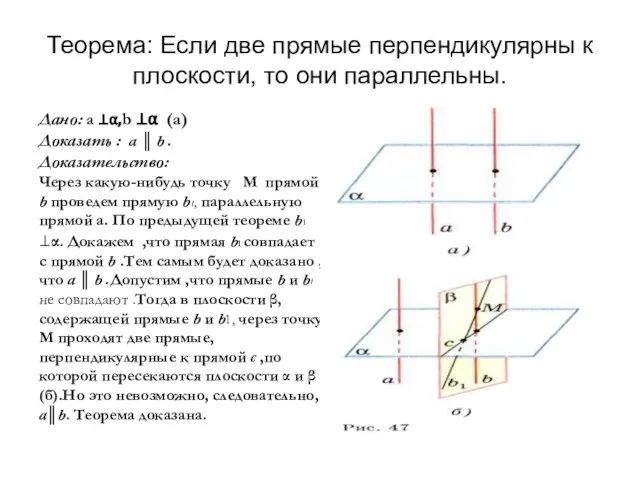
Теорема: Если две прямые перпендикулярны к плоскости, то они параллельны.
Дано: a ⊥α,b ⊥α (а)
Доказать : a ║ b .
Доказательство:
Через какую-нибудь точку M прямой b проведем прямую b1, параллельную прямой a. По предыдущей теореме b1 ⊥α. Докажем ,что прямая b1 совпадает с прямой b .Тем самым будет доказано ,что a ║ b .Допустим ,что прямые b и b1 не совпадают .Тогда в плоскости β,содержащей прямые b и b1, через точку М проходят две прямые, перпендикулярные к прямой c ,по которой пересекаются плоскости α и β (б).Но это невозможно, следовательно, a║b. Теорема доказана.