Первомайский район Володарская средняя общеобразовательная школа полного дня.

Совершенствование навыков самостоятельной деятельности учащихся при решении задач на оптимизацию в средней школе.
Актуальность данной проблемы, потребности практики и недостаточная освещенность в методической литературе побудили обратиться к более тщательному её рассмотрению.
Объектом исследования является организационно-педагогическая и учебная деятельности общеобразовательной школы, направленные на осуществление профильной дифференциации обучения в процессе преподавания математики.

Предмет исследования - совершенствование видов самостоятельной деятельности в свете реализации требований современной концепции образования
Цели:
На основе выявления организационно – педагогических закономерностей и определения оптимальных путей решения поставленных задач сформулировать рекомендации по организации видов самостоятельной деятельности при изучении данной темы.
Задачи:
Раскрыть психолого – педагогические основы осуществления дифференциации.
Определить оптимальные пути взаимодействия участников педагогического процесса.
Постараться обосновать возможность совершенствования учебно – воспитательного процесса применительно к процессу преподавания математики.

Задачи на оптимизацию в значительной степени способствуют развитию самостоятельности учащихся, они относятся к числу как наиболее трудных, так и наиболее интересных задач.
Самостоятельная деятельность учащихся повышает эффективность обучения лишь в том случае, когда учителем проведена рациональная её организация.
С целью создания проблемной ситуации перед учащимися обращается внимание на важность усвоения алгоритма решения задач на оптимизацию и дальнейшее его воспроизведение:
1 этап – составление математической модели,
2 этап – работа с составленной моделью,
3 этап – ответ на вопрос задачи.

Особое внимание уделяется самостоятельному осмыслению учащимися действий внутри этапов решения задачи:
Методика работы с задачей (мотивационный этап)
Анализ условия
Мысленная модель задачи
Математическое моделирование
Решение задачи внутри модели
Критическое осмысление полученного результата.

Три этапа в решении задачи можно считать полностью завершёнными, если учащиеся хорошо будут представлять:
структуру математической задачи,
процесс решения задачи,
ведущую математическую идею процесса решения задачи

Применение мультимедийной установки дает возможность оживить действия и получить не только теоретические знания, но и проверить результаты, независимо от оценки учителя.
Внедрение в учебный процесс компьютера позволяет оптимизировать труд учителя и повысить эффективность обучения;

Тренажер.
Задача: найдите размеры участка прямоугольной формы, имеющего наибольшую площадь, если его периметр равен 400м.
Пусть ширина прямоугольника х м., а длина у м.
Р=2(х+у), 2(х+у)=400, х+у=200, у=200-х, 0<х<200.
Составьте формулу исследуемой функции:
S(x)=xy=x(200-x)=200x-x² и найдите наибольшее значение этой функции на отрезке [0;200].
Найдите критические точки функции:
S(x)=200x-x², S‘(x)=200-2х, S‘(x)=0, т.е 200-2х=0 и х=100.
Найдите значение функции на концах отрезка и в критических точках S(0)=0, S(100)=10000,S(200)=0.
Значит, наибольшей будет площадь участка 10000 м².

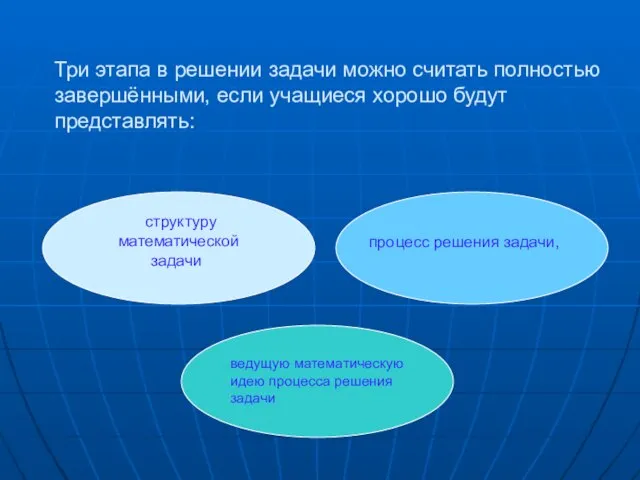
Формирование навыков самостоятельной деятельности учащихся помогает обеспечивать успешность учебной деятельности, выявлять зависимость между формированием опорных знаний и активностью учебной деятельности школьников в дифференцированном обучении, что ведет к развитию способов учебно – познавательной деятельности, обеспечивающих успешность их выполнения.
С целью совершенствования навыков самостоятельной деятельности учащихся при изучении данной темы следует продумать и определить:
1 цель, время и характер самостоятельной работы, а также те формируемые навыки самостоятельного изучения математики, на которые можно обратить внимание учащихся при выполнении работы,
2 способ повторения того минимума фактических знаний и умений, без которых невозможно успешное выполнение данной самостоятельной работы.
3 выполнение заданий репродуктивного или продуктивного характера, или заданий на повторение, а также сопутствующие им умения,
4 методику устранения возможных затруднений в ходе выполнения заданий, способ быстрой проверки полученных результатов и методику разбора допущенных ошибок.