Площадь криволинейной трапеции и интеграл

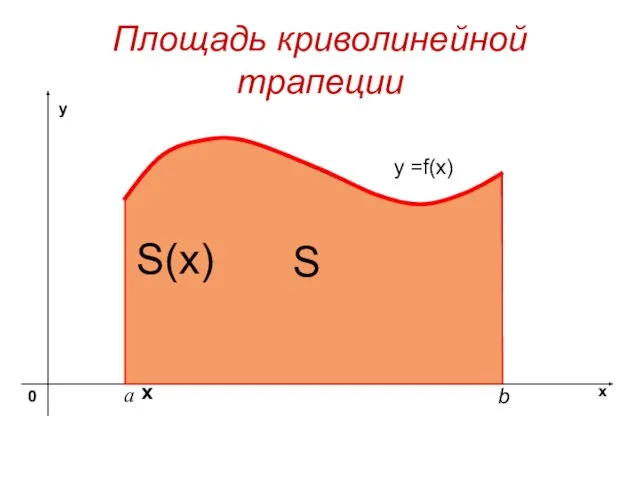
Площадь криволинейной трапеции
y =f(x)
S
х
S(x)

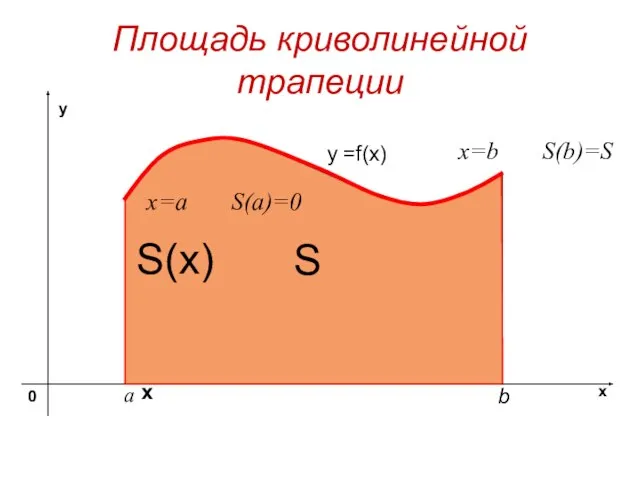
Площадь криволинейной трапеции
y =f(x)
S
х
S(x)
x=a S(a)=0
x=b S(b)=S

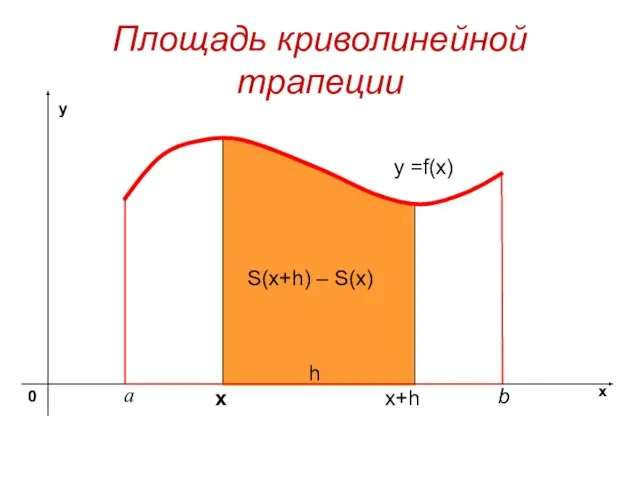
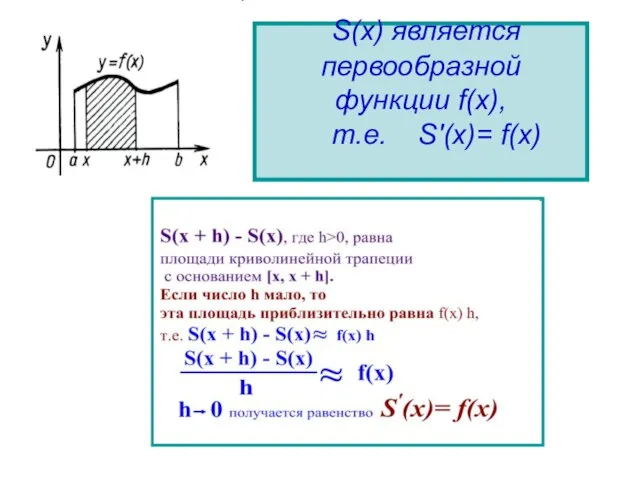
Площадь криволинейной трапеции
y =f(x)
х
S(x+h) – S(x)
x+h
h

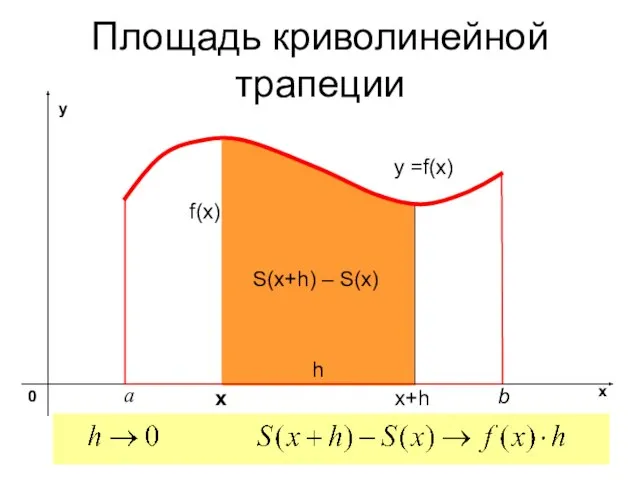
Площадь криволинейной трапеции
y =f(x)
х
S(x+h) – S(x)
x+h
h
f(x)

Площадь криволинейной трапеции

Фигура, ограниченная снизу отрезком [a, b] оси Ох ,сверху графиком непрерывной функции у= f(x), принимающей положительные значения , а с боков отрезками прямых х = а, х =b называется криволинейной трапецией.

Обозначим S(х) - площадь криволинейной трапеции с основанием [a, х] , х - любая точка отрезка [a, b]
При х = а отрезок [a, х] вырождается в
точку, поэтому S(а) = 0; при х = b,
S(b) = S

S(х) является
первообразной функции f(x), т.е. S'(х)= f(x)

Площадь криволинейной трапеции
вычисляется по формуле
S = F(b) - F(a)
Разность F(b) - F(a) называют
интегралом от функции f(x)
на отрезке [a, b] и обозначают так :

Любая другая первообразная F(x)
отличается от S(x) на постоянную,
т.е. F(x) = S(x) + С
При х = а получаем F(a) = S(a) + C
Так как S(a) = 0 , то С = F(a) и равенство
F(x) = S(x) + С можно записать так
S(x) = F(x) - F(a), отсюда при х =b получим
S(b) = F(b) - F(a)

Немного истории
-1675 г, опубликовано в 1686 г
ввел Г.Лейбниц
- 1675 г, Ж Лагранж
5 век до н.э. др.гр. ученый Демокрит
3-4 век до н.э. Архимед ввел метод исчерпывания

Лейбниц Готфрид Вильгельм
(1646-1716)
« Общее искусство знаков представляет чудесное пособие, так как оно разгружает воображение… Следует заботиться о том, чтобы обозначения были удобны для открытий. Обозначения коротко выражают и отображают сущность вещей. Тогда поразительным образом сокращается работа мысли.»
Лейбниц

Исаак Ньютон
(1643-1727)
Разумом он превосходил род человеческий. Лукреций

Немного истории
«Интеграл» придумал Я.Бернулли (1690)
«восстанавливать» от латинского integro
«целый» от латинского integer

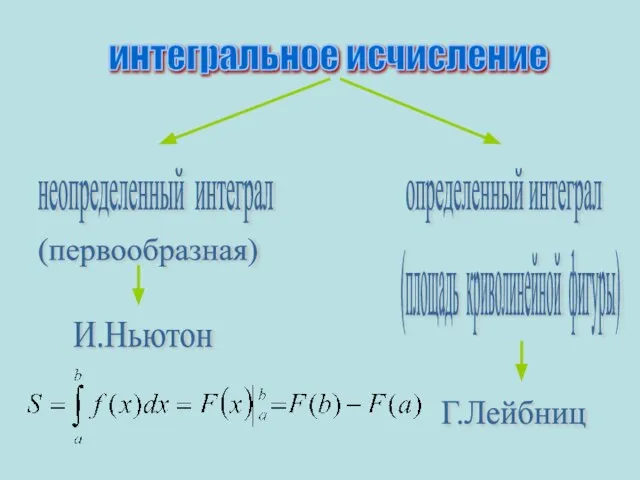
интегральное исчисление
неопределенный интеграл
определенный интеграл
(первообразная)
(площадь криволинейной фигуры)
И.Ньютон
Г.Лейбниц

Применение интеграла
Площадь фигуры
Объем тела вращения
Работа электрического заряда
Работа переменной силы
Центр масс

В классе:
№ 999(1,3)
№ 1000(1,2)