Построение сечений пирамиды (тетраэдра)

«Воображение важнее знания. Знание ограничено, воображением можно охватить всё» А. Эйнштейн

Виды деятельности
1. Целеполагание
2. Теоретическая основа
3. Устная работа
4. Тест. Работа в паре.
5. Практикум. Коллективная работа.
6. Самостоятельная работа с самопроверкой
7. Инструктаж домашнего задания
8. Работа в группах: «Составь задачу»
9. Рефлексия. Самооценка своей работы.

1.Цель урока
Цель- конечный желаемый результат
Напиши свою цель урока

1. Цель урока
Научиться строить сечения тетраэдра

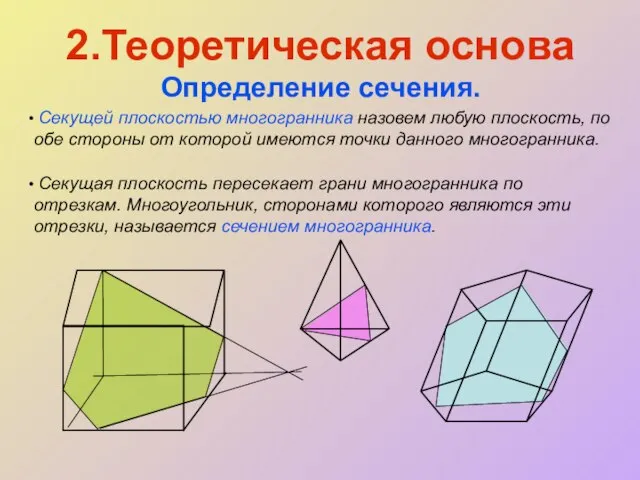
2.Теоретическая основа Определение сечения.
Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника.
Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

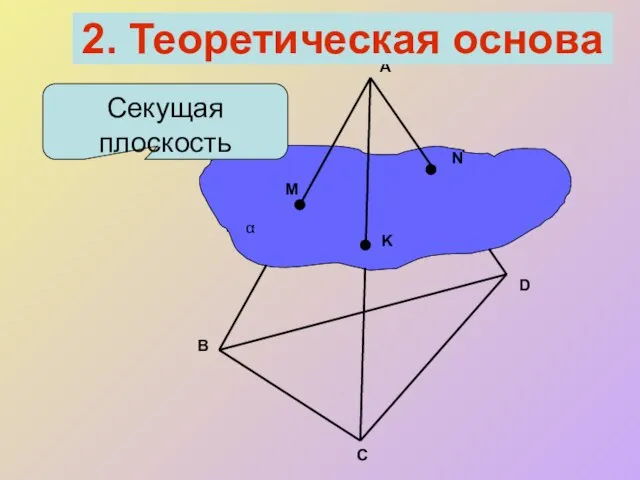
Секущая плоскость
А
В
С
D
M
N
K
α
2. Теоретическая основа

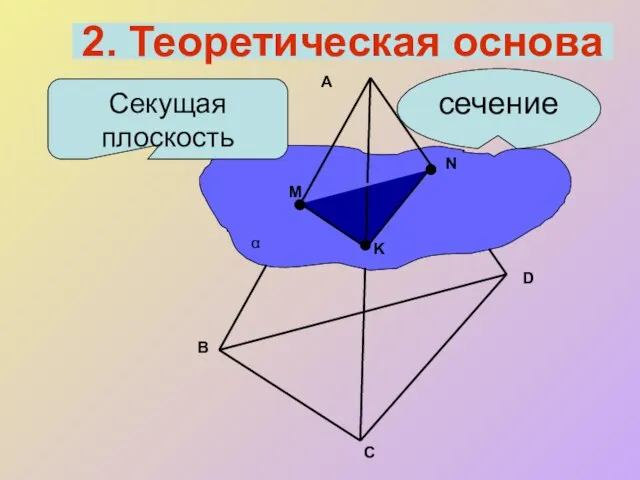
Секущая плоскость
сечение
A
B
C
D
M
N
K
α
2. Теоретическая основа

2.Теоретическая основа Геометрические утверждения
Если две точки одной прямой лежат в плоскости, то и
вся прямая лежит в этой плоскости.

2. Теоретическая основа Геометрические утверждения
Если две параллельные плоскости пересечены третьей, то
линии их пересечения параллельны.

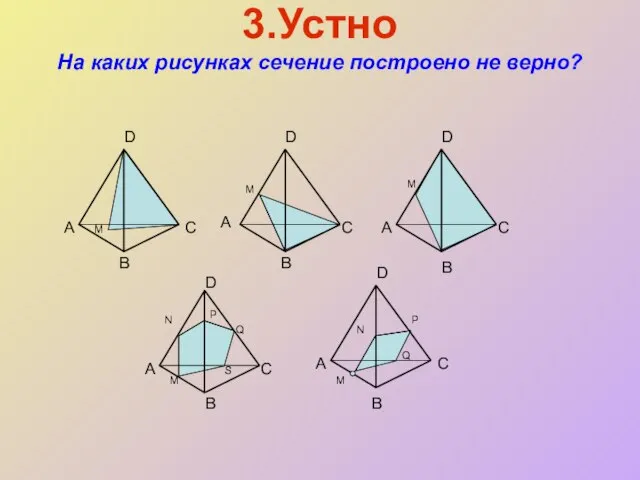
3.Устно На каких рисунках сечение построено не верно?
B
А
А
А
А
А
D
D
D
D
D
B
B
B
B
C
C
C
C
C
N
M
M
M
M
M
N
Q
P
P
Q
S

3. Устно
Объясните, какая теория использована
при построении следующих сечений

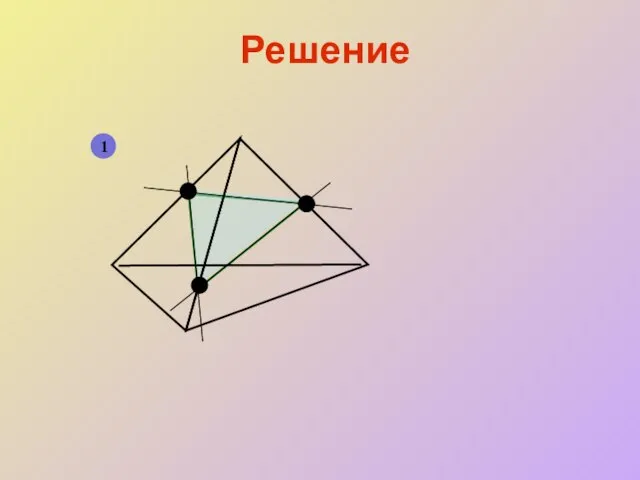
Решение
1

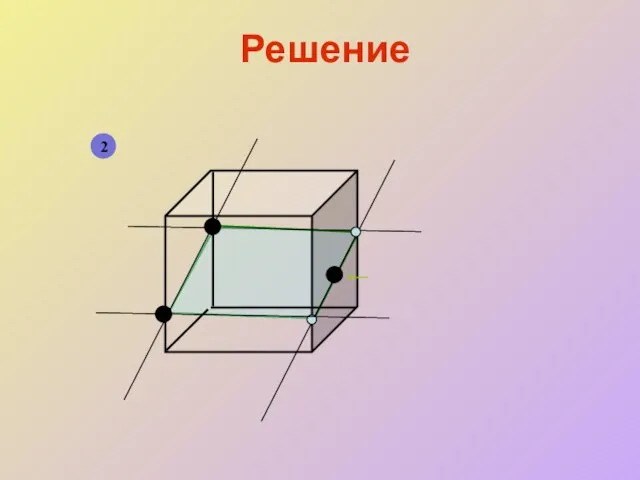
Решение
2

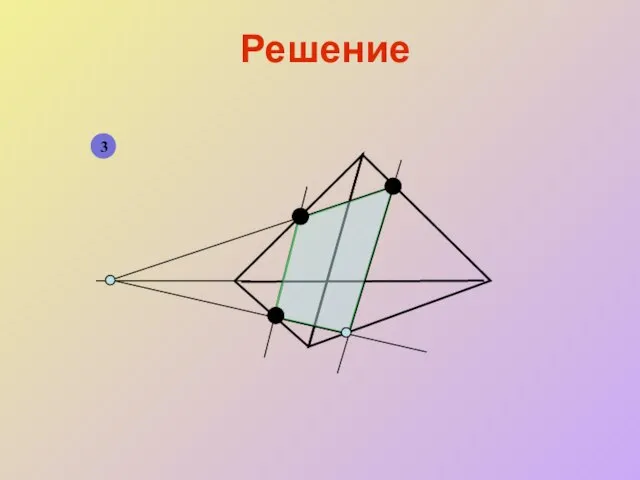
Решение
3

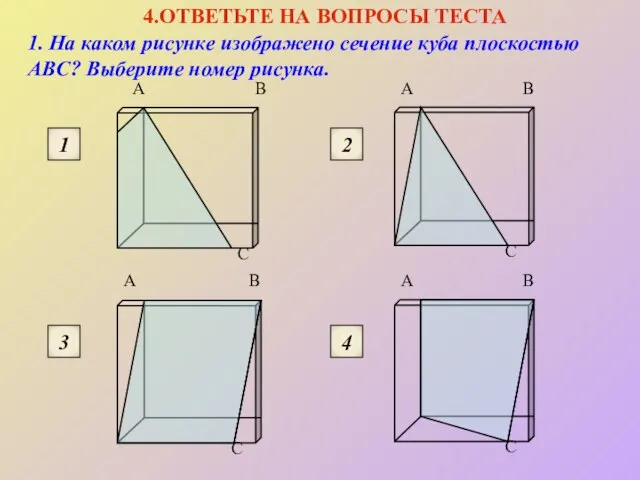
4.ОТВЕТЬТЕ НА ВОПРОСЫ ТЕСТА
1. На каком рисунке изображено сечение куба плоскостью ABC? Выберите номер рисунка.
1
3
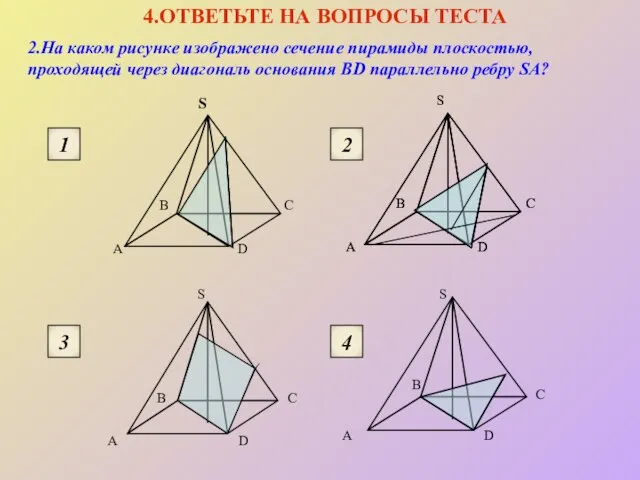
2
4

2.На каком рисунке изображено сечение пирамиды плоскостью, проходящей через диагональ основания BD параллельно ребру SA?
4.ОТВЕТЬТЕ НА ВОПРОСЫ ТЕСТА
1
3
2
4

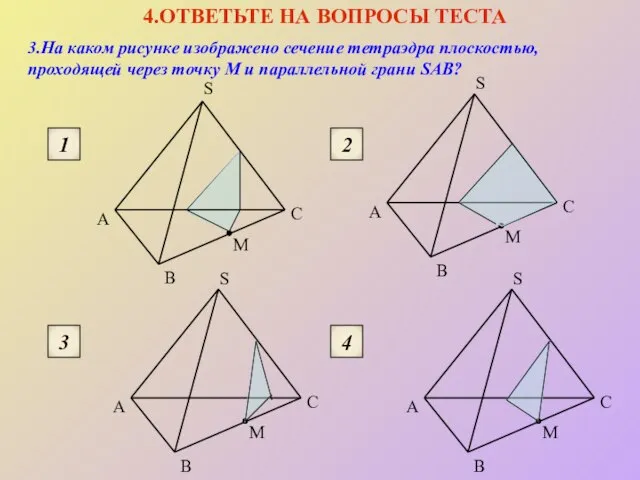
3.На каком рисунке изображено сечение тетраэдра плоскостью, проходящей через точку М и параллельной грани SAВ?
4.ОТВЕТЬТЕ НА ВОПРОСЫ ТЕСТА
1
3
2
4
S
S
B
B

Код теста
324

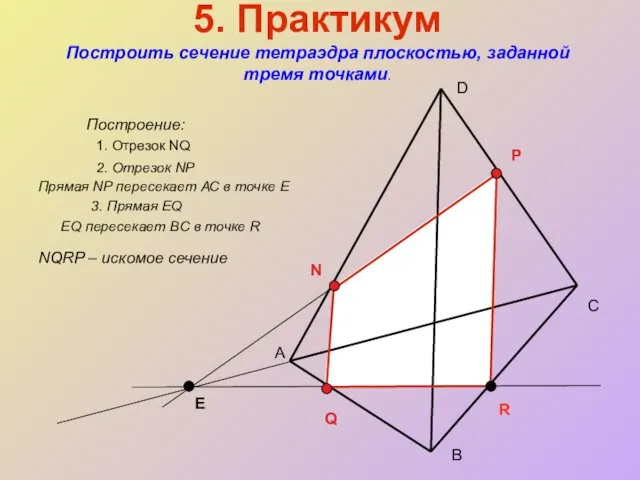
5. Практикум Построить сечение тетраэдра плоскостью, заданной тремя точками.
Построение:
А
С
В
D
N
P
Q
R
E
1. Отрезок NQ
2. Отрезок NP
Прямая NP пересекает АС в точке Е
3. Прямая EQ
EQ пересекает BC в точке R
NQRP – искомое сечение

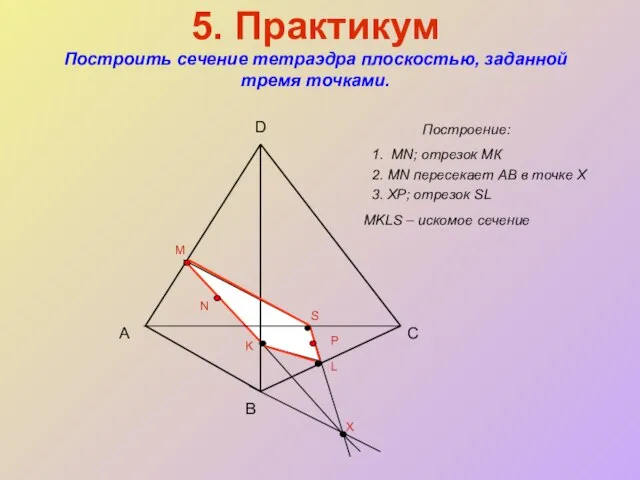
5. Практикум Построить сечение тетраэдра плоскостью, заданной тремя точками.
Построение:
А
B
C
D
M
N
P
X
K
S
L
1. MN; отрезок МК
2. MN пересекает АВ в точке Х
3. ХР; отрезок SL
MKLS – искомое сечение

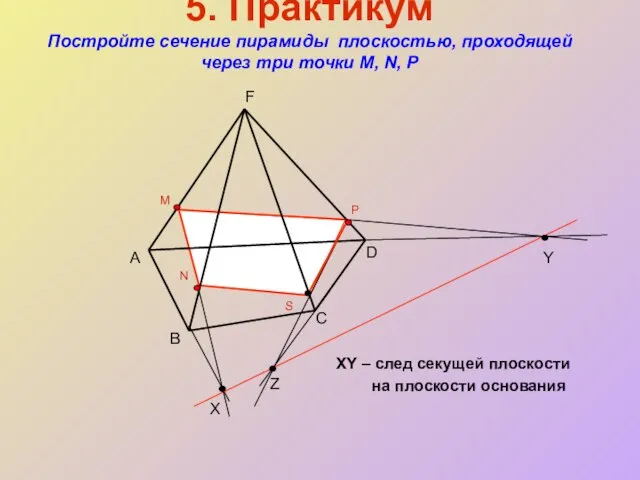
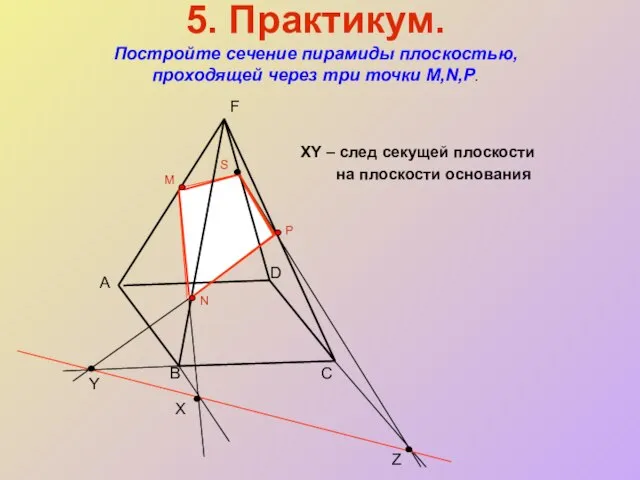
5. Практикум Постройте сечение пирамиды плоскостью, проходящей через три точки М, N, Р
XY – след секущей плоскости
на плоскости основания
D
C
B
А
Z
Y
X
M
N
P
S
F

XY – след секущей плоскости
на плоскости основания
D
C
B
Z
Y
X
M
N
P
S
5. Практикум. Постройте сечение пирамиды плоскостью,
проходящей через три точки M,N,P.
А
F

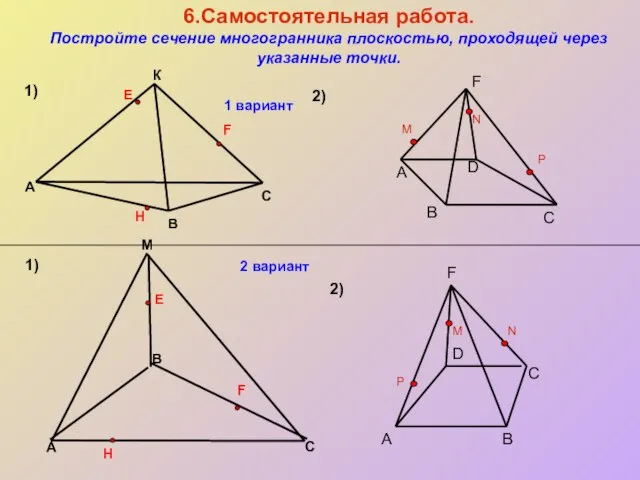
6.Самостоятельная работа. Постройте сечение многогранника плоскостью, проходящей через указанные точки.
M
A
1)
1)
2)
2)
В
С
К
В
A
С
E
F
H
E
H
F
1 вариант
2 вариант
D
C
B
M
N
P
А
F
D
C
B
M
N
P
А
F

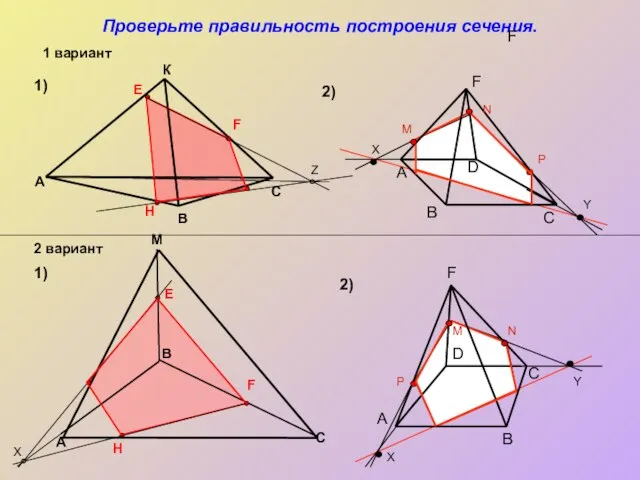
Проверьте правильность построения сечения.
M
A
1)
1)
2)
2)
В
С
К
В
A
С
E
F
H
E
H
F
1 вариант
2 вариант
D
C
B
M
N
P
А
F
F
X
Y
Z
X
D
C
B
M
N
P
А
F
X
Y

7. Творческое домашнее задание
Составить 3-4 задачи на построение сечений многогранников.
Выполнить решения в форме презентации или в WORDE. Срок до 10 дней.
Критерии оценки:
Сложность
Правильность решения
Дизайн

8. Работа в группах
Задайте плоскость сечения куба 3-мя точками так, чтобы она не пересекала только
1группа: верхнюю грань
2группа: правую грань
3 группа: левую грань
4 группа: нижнюю грань
Постройте заданное вами сечение

9. Подведение итогов работы на уроке
Критерии самооценки:
Тест 0,1,2,3 балла «5» - 15 баллов +
Устная работа 1-2 балла «4» - 10-14 баллов
Практикум 1-3балла
Сам. работа 3; 5 баллов
Сост. задачи 3-5 баллов
В чём я вижу результат своей работы?
Что мне помогло достичь результата?

Китайская пословица
Не бойся, что не знаешь - бойся, что не учишься.