Площади фигур

Содержание
Основные свойства площадей геометрических фигур.
Площадь квадрата.
Площадь прямоугольника.
Площадь параллелограмма.
Площадь треугольника.
Площадь треугольника.
Площадь трапеции.
ТЕСТ.
Список литературы.

Основные свойства площадей
геометрических фигур
Любая плоская геометрическая фигура имеет площадь. Эта площадь – единственная.
Площадь любой геометрической фигуры выражается положительным числом.
Площадь квадрата со стороной,равной единице,равна единице.
Площадь фигуры равна сумме площадей частей,на которые она разбивается.
Равные многоугольники имеют равные площади.

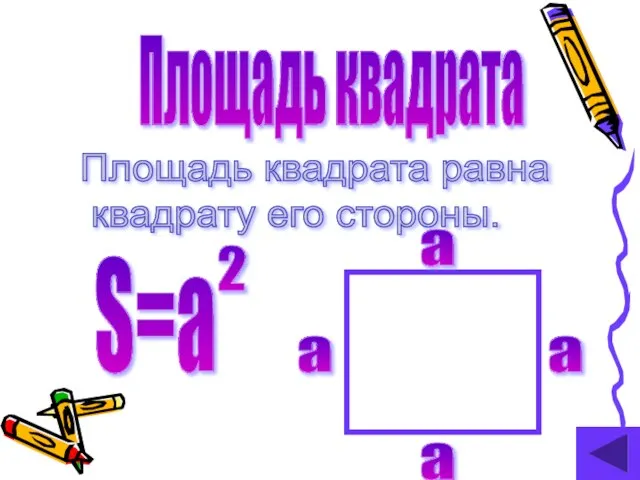
Площадь квадрата
Площадь квадрата равна квадрату его стороны.
а
а
а
а
S=a
2

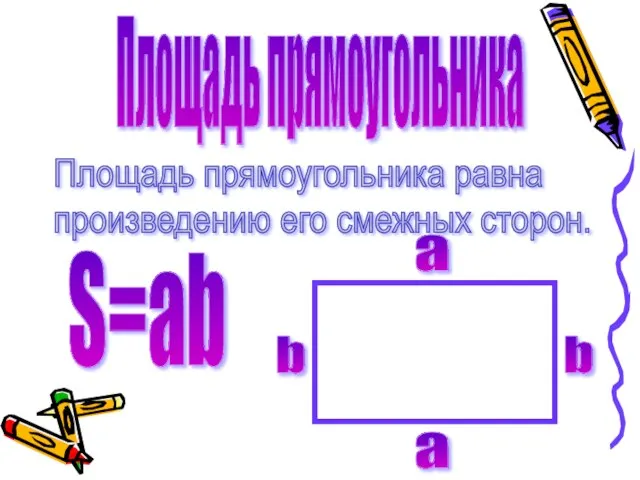
Площадь прямоугольника
Площадь прямоугольника равна
произведению его смежных сторон.
а
а
S=ab
b
b

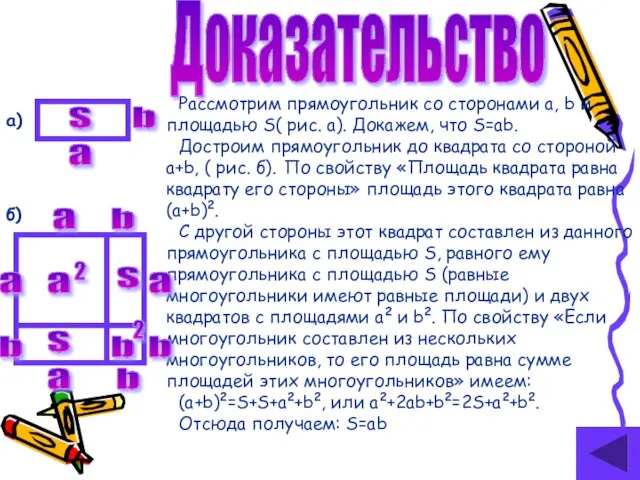
Доказательство
Рассмотрим прямоугольник со сторонами a, b и площадью S( рис. а). Докажем, что S=ab.
Достроим прямоугольник до квадрата со стороной a+b, ( рис. б). По свойству «Площадь квадрата равна квадрату его стороны» площадь этого квадрата равна (a+b)2.
С другой стороны этот квадрат составлен из данного прямоугольника с площадью S, равного ему прямоугольника с площадью S (равные многоугольники имеют равные площади) и двух квадратов с площадями a2 и b2. По свойству «Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников» имеем:
(a+b)2=S+S+a2+b2, или a2+2ab+b2=2S+a2+b2.
Отсюда получаем: S=ab
а
b
а)
b
b
b
b
а
а
а
а
а
2
b
S
S
S
б)
2

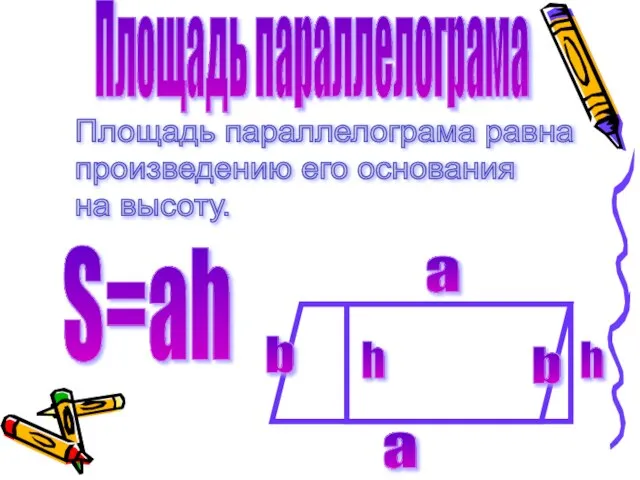
Площадь параллелограма
Площадь параллелограма равна
произведению его основания
на высоту.
а
а
h
h
S=ah
b
b

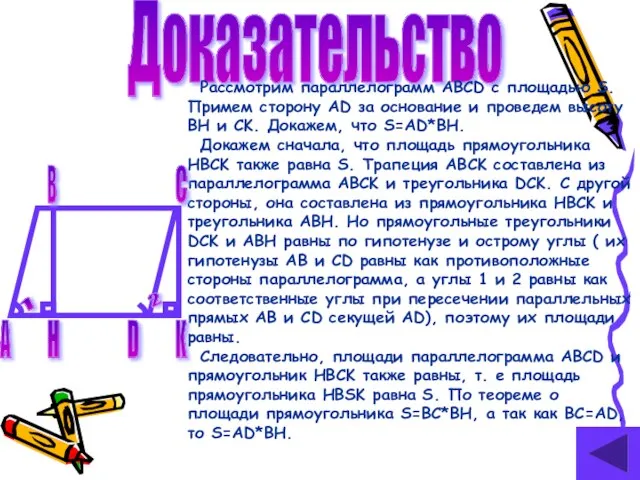
Доказательство
Рассмотрим параллелограмм ABCD с площадью S. Примем сторону AD за основание и проведем высоту BH и CK. Докажем, что S=AD*BH.
Докажем сначала, что площадь прямоугольника HBCK также равна S. Трапеция ABCK составлена из параллелограмма ABCK и треугольника DCK. С другой стороны, она составлена из прямоугольника HBCK и треугольника ABH. Но прямоугольные треугольники DCK и ABH равны по гипотенузе и острому углы ( их гипотенузы AB и CD равны как противоположные стороны параллелограмма, а углы 1 и 2 равны как соответственные углы при пересечении параллельных прямых AB и CD секущей AD), поэтому их площади равны.
Следовательно, площади параллелограмма ABCD и прямоугольник HBCK также равны, т. е площадь прямоугольника HBSK равна S. По теореме о площади прямоугольника S=BC*BH, а так как BC=AD, то S=AD*BH.
C
B
K
A
H
D
1
2

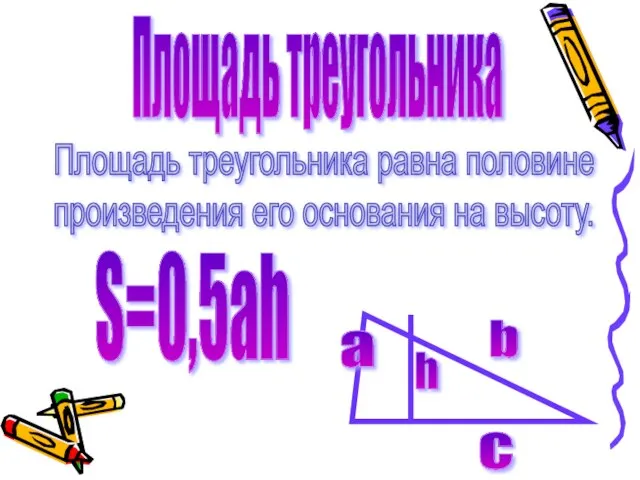
Площадь треугольника
Площадь треугольника равна половине
произведения его основания на высоту.
а
с
h
S=0,5ah
b

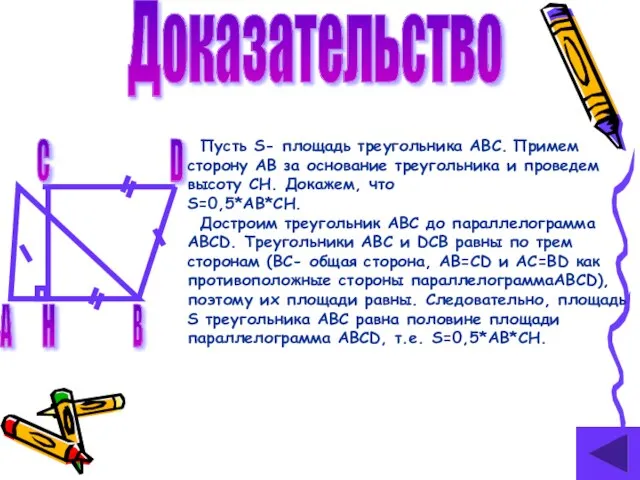
Доказательство
Пусть S- площадь треугольника ABC. Примем сторону AB за основание треугольника и проведем высоту CH. Докажем, что S=0,5*AB*CH.
Достроим треугольник ABC до параллелограмма ABCD. Треугольники ABC и DCB равны по трем сторонам (BC- общая сторона, AB=CD и AC=BD как противоположные стороны параллелограммаABCD), поэтому их площади равны. Следовательно, площадь S треугольника ABC равна половине площади параллелограмма ABCD, т.е. S=0,5*AB*CH.
C
B
A
H
D

Площадь треугольника
Площадь треугольника равна половине
произведения двух его сторон на синус
угла между ними.
C
B
A (b cos C; b sin C)
с
а
h
S=0.5a b sinC
b

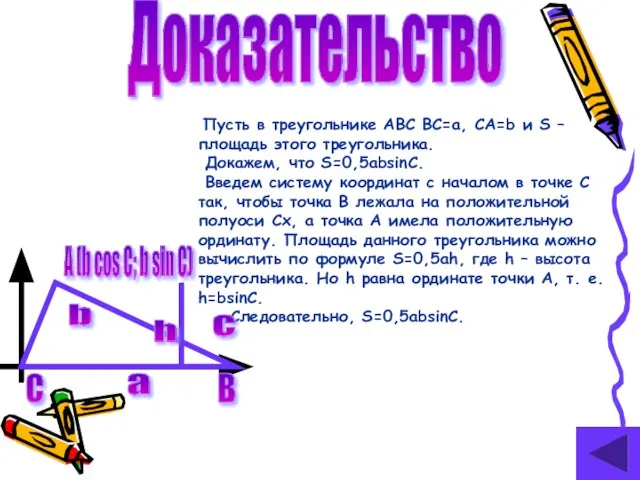
Доказательство
Пусть в треугольнике ABC BC=a, CA=b и S – площадь этого треугольника.
Докажем, что S=0,5absinC.
Введем систему координат с началом в точке С так, чтобы точка В лежала на положительной полуоси Сх, а точка А имела положительную ординату. Площадь данного треугольника можно вычислить по формуле S=0,5ah, где h – высота треугольника. Но h равна ординате точки А, т. е. h=bsinC.
Следовательно, S=0,5absinC.
C
A (b cos C; b sin C)
а
b
B
c
h

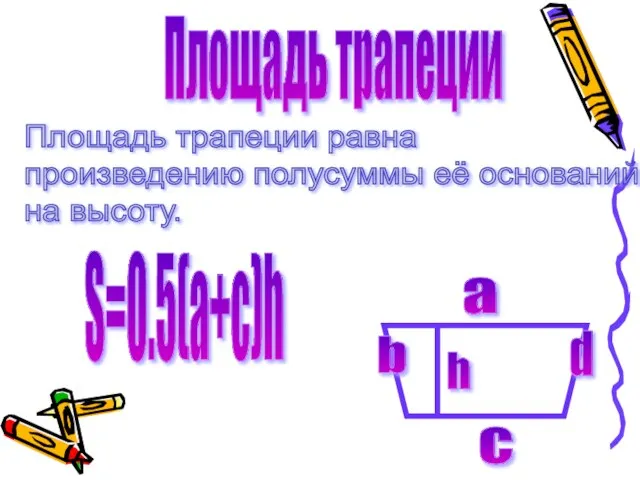
Площадь трапеции
Площадь трапеции равна
произведению полусуммы её оснований
на высоту.
h
а
с
d
S=0.5(a+c)h
b

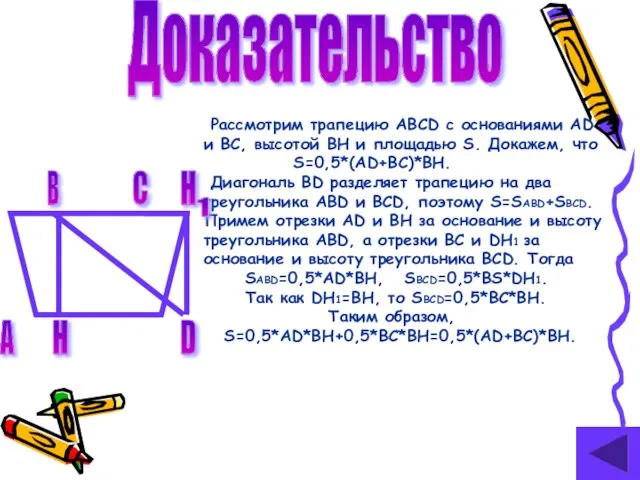
Доказательство
Рассмотрим трапецию ABCD с основаниями AD и BC, высотой BH и площадью S. Докажем, что
S=0,5*(AD+BC)*BH.
Диагональ BD разделяет трапецию на два треугольника ABD и BCD, поэтому S=SABD+SBCD. Примем отрезки AD и BH за основание и высоту треугольника ABD, а отрезки BC и DH1 за основание и высоту треугольника BCD. Тогда
SABD=0,5*AD*BH, SBCD=0,5*BS*DH1.
Так как DH1=BH, то SBCD=0,5*BC*BH.
Таким образом,
S=0,5*AD*BH+0,5*BC*BH=0,5*(AD+BC)*BH.
C
B
A
H
D
H
1

Найдите площадь геометрической фигуры
Тест
а) 560
b) 576
c) 476
d) 519
24

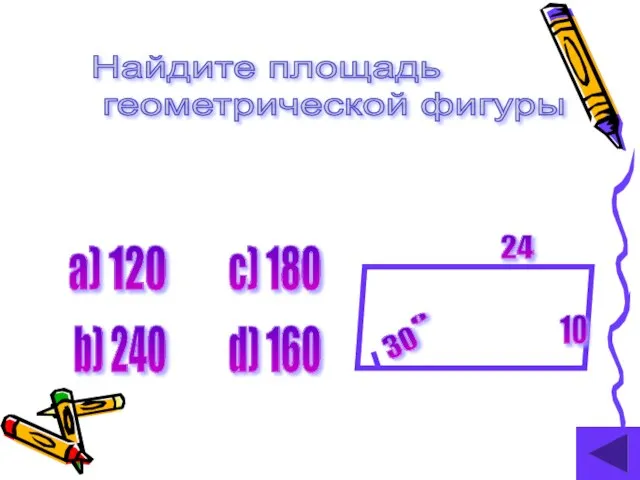
Найдите площадь геометрической фигуры
30
0
24
10
а) 120
b) 240
c) 180
d) 160

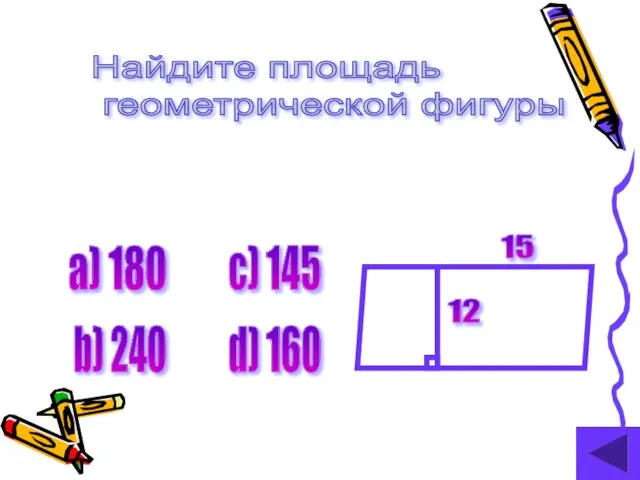
Найдите площадь геометрической фигуры
а) 180
b) 240
c) 145
d) 160
15
12

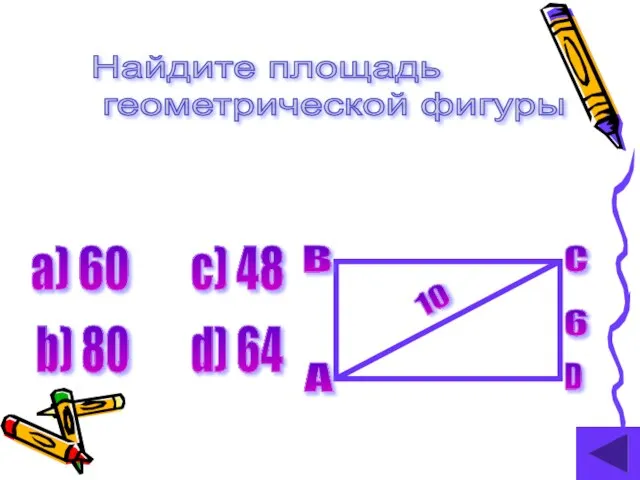
Найдите площадь геометрической фигуры
10
6
а) 60
b) 80
c) 48
d) 64
B
A
C
D

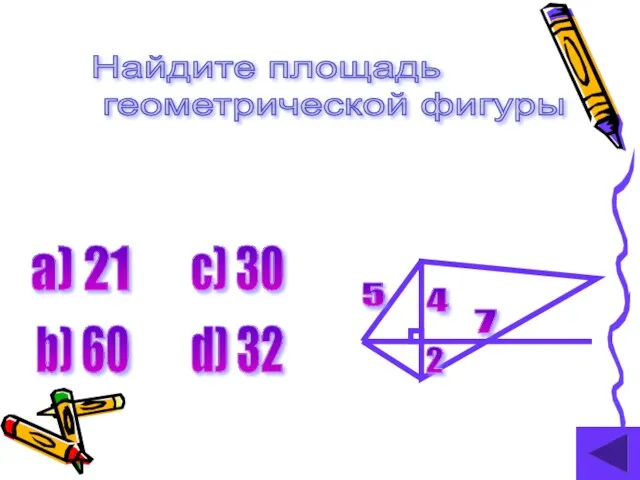
Найдите площадь геометрической фигуры
7
4
2
5
а) 21
b) 60
c) 30
d) 32

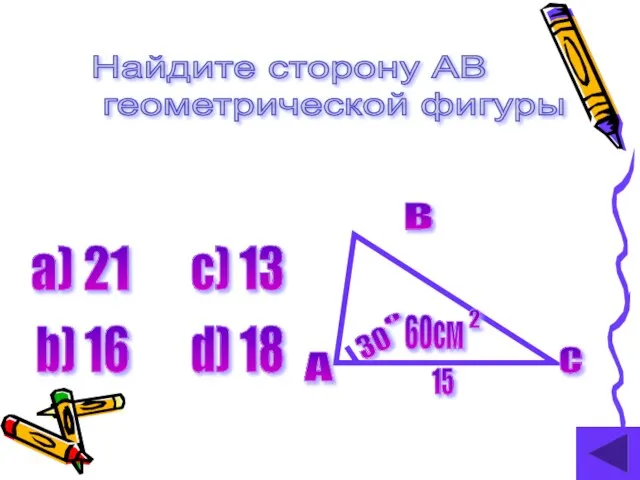
Найдите сторону AB геометрической фигуры
а) 21
b) 16
c) 13
d) 18
A
B
C
15
30
0
60см
2

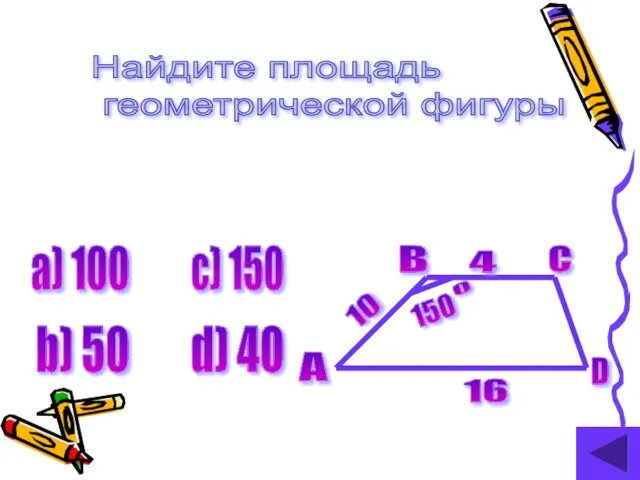
Найдите площадь геометрической фигуры
16
10
4
A
150
0
B
C
D
а) 100
b) 50
c) 150
d) 40

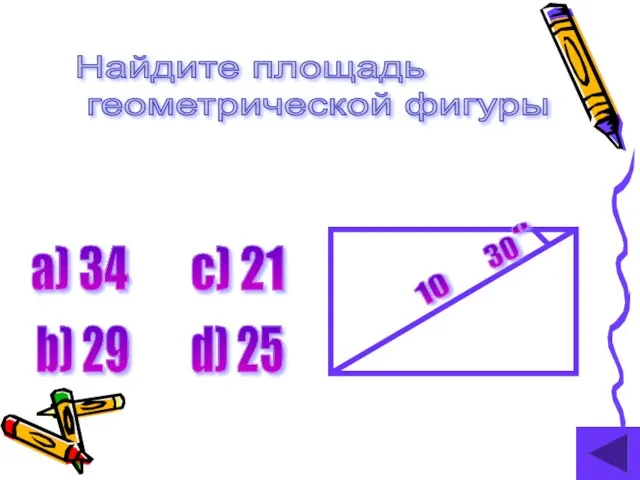
Найдите площадь геометрической фигуры
а) 34
b) 29
c) 21
d) 25
10
30
0

Список литературы
http://fio.ifmo.ru/archive/group13/c2wu5/text/test/tes9/test9.htm
Геометрия, 7-9: Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.- 14-е изд. – М.: Просвещение, 2004.- 384 с.: ил..

Правильно