Содержание
- 2. Плоская система сил Линии действия всех сил лежат в одной плоскости Пространственная система сил − если
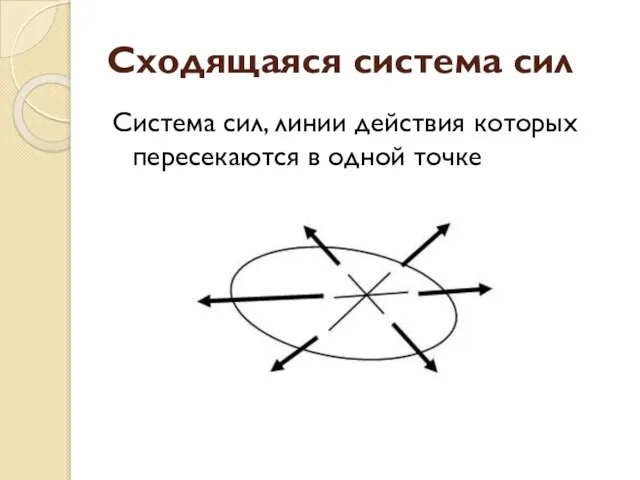
- 3. Сходящаяся система сил Система сил, линии действия которых пересекаются в одной точке
- 4. Система сходящихся сил эквивалентна одной силе – равнодействующей, которая равна векторной сумме сил приложена в точке
- 5. МЕТОДЫ ОПРЕДЕЛЕНИЯ РАВНОДЕЙСТВУЮЩЕЙ
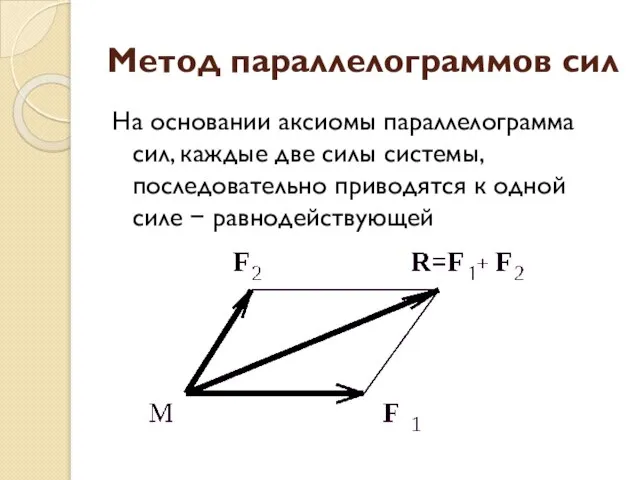
- 6. Метод параллелограммов сил На основании аксиомы параллелограмма сил, каждые две силы системы, последовательно приводятся к одной
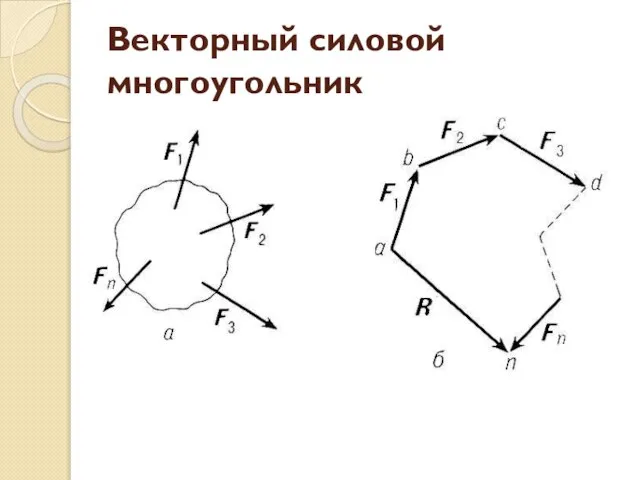
- 7. Векторный силовой многоугольник Поочерёдно откладываем каждый вектор силы от конечной точки предыдущего вектора Получаем многоугольник: стороны
- 8. Векторный силовой многоугольник
- 9. Условия равновесия системы сходящихся сил Геометрическое условие для равновесия системы сходящихся сил необходимо и достаточно, чтобы
- 10. Условия равновесия системы сходящихся сил Аналитические условия Для равновесия системы сходящихся сил необходимо и достаточно, чтобы
- 11. РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ГЕОМЕТРИЧЕСКИМ СПОСОБОМ
- 12. Геометрический способ Удобен , если в системе три силы Тела считаются абсолютно твёрдым
- 13. Алгоритм 1. Определить возможное направление реакций связей 2. Вычертить многоугольник сил системы, начиная с известных сил
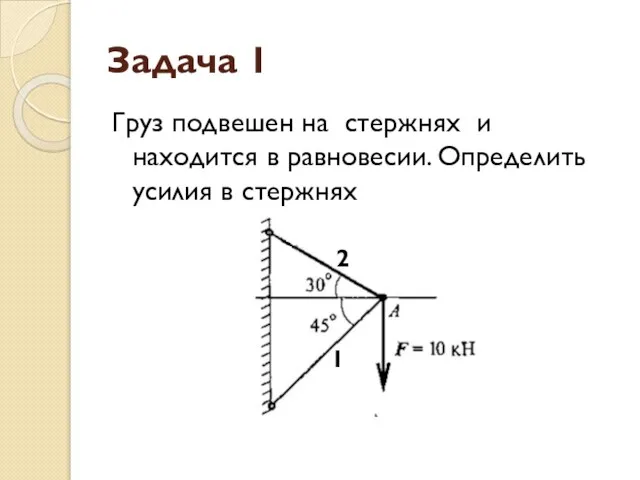
- 14. Задача 1 Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях 1 2
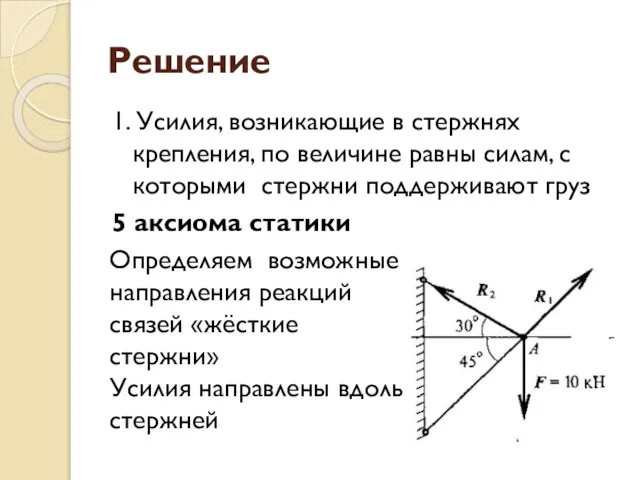
- 15. Решение 1. Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз
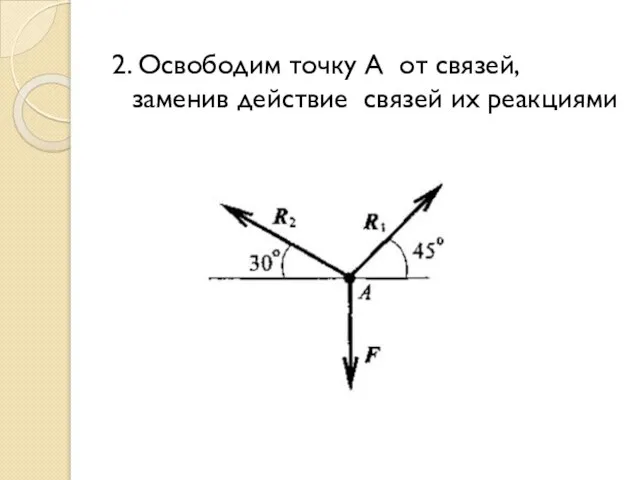
- 16. 2. Освободим точку А от связей, заменив действие связей их реакциями
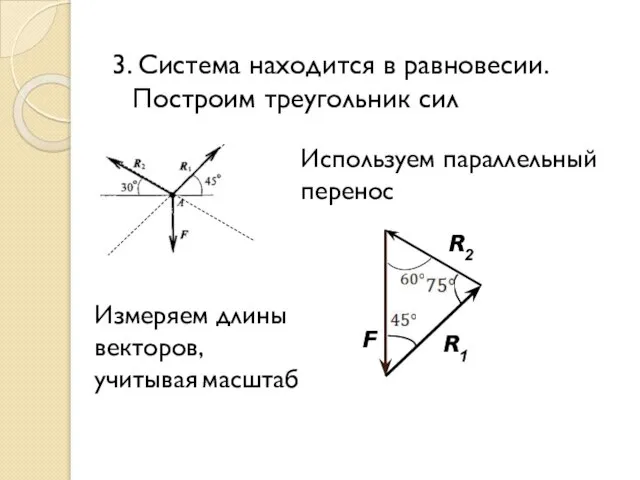
- 17. 3. Система находится в равновесии. Построим треугольник сил F R1 R2 Используем параллельный перенос Измеряем длины
- 18. 4. Для точности расчётов используем теоремой синусов Для данного случая
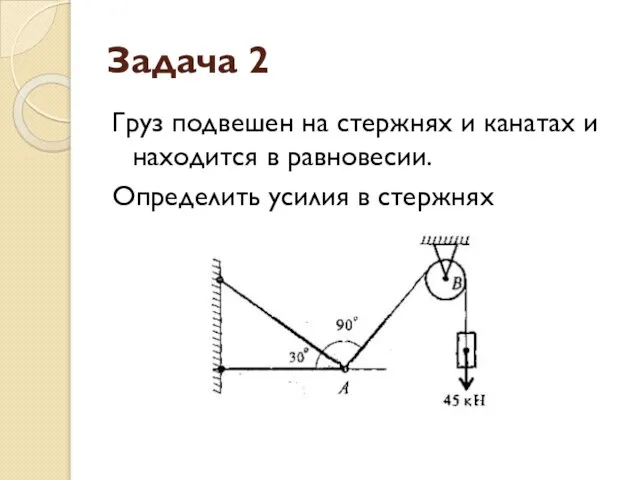
- 19. Задача 2 Груз подвешен на стержнях и канатах и находится в равновесии. Определить усилия в стержнях
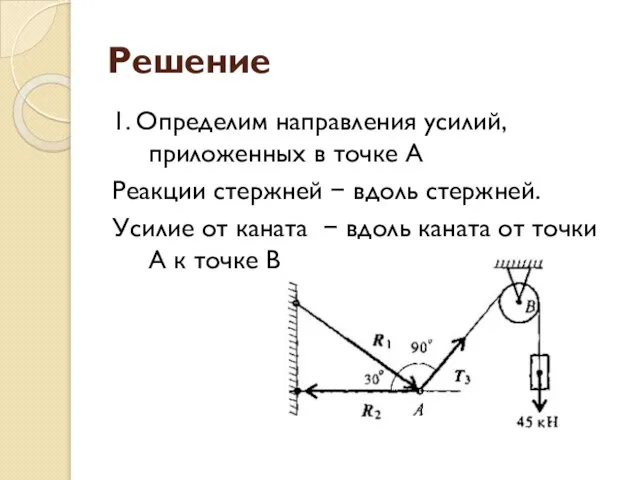
- 20. Решение 1. Определим направления усилий, приложенных в точке А Реакции стержней − вдоль стержней. Усилие от
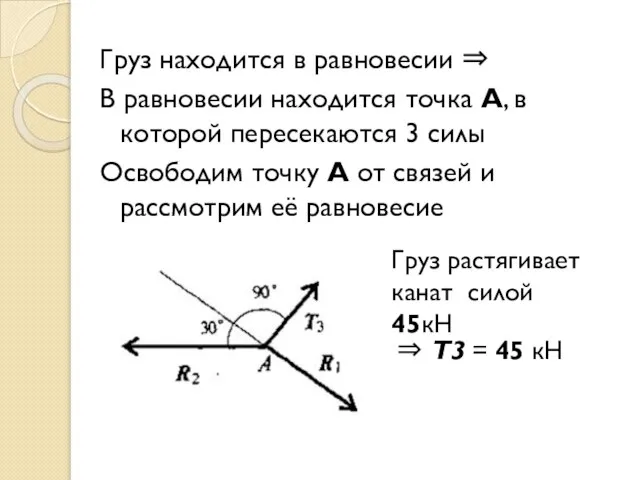
- 21. Груз находится в равновесии ⇒ В равновесии находится точка А, в которой пересекаются 3 силы Освободим
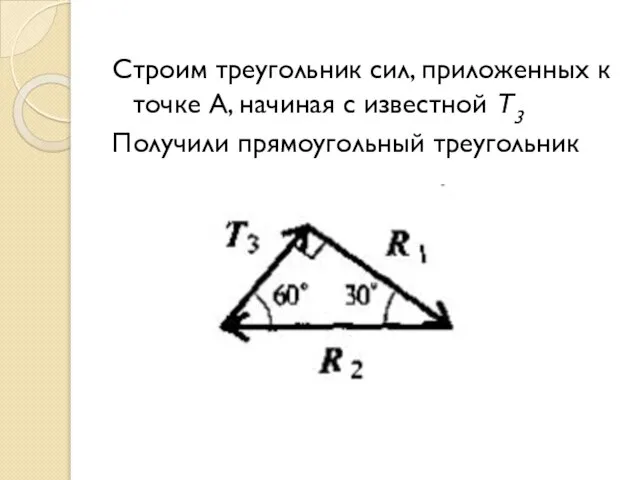
- 22. Строим треугольник сил, приложенных к точке А, начиная с известной T3 Получили прямоугольный треугольник
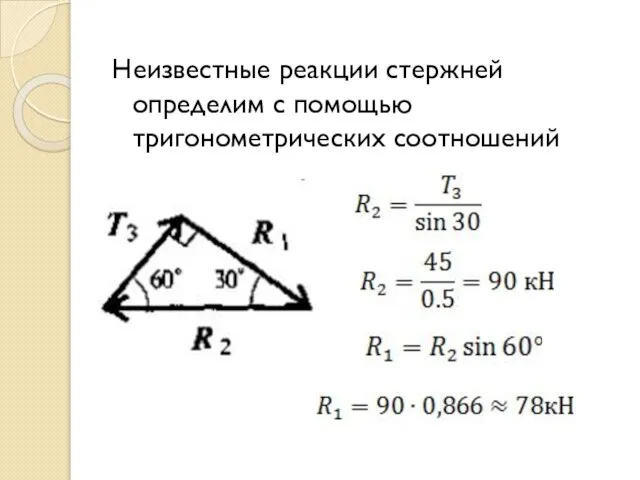
- 23. Неизвестные реакции стержней определим с помощью тригонометрических соотношений
- 24. Проекция силы на ось Определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца
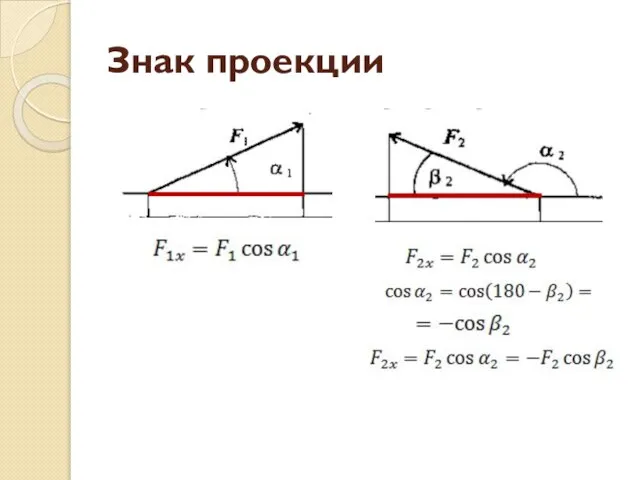
- 25. Знак проекции
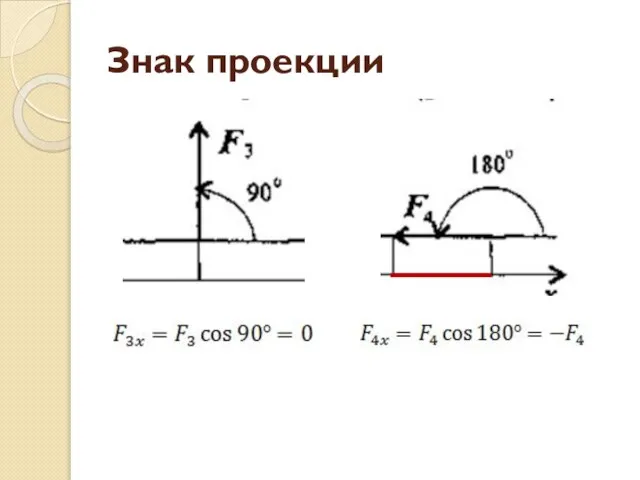
- 26. Знак проекции
- 27. Проекция силы на 2 взаимно перпендикулярные оси
- 28. ОПРЕДЕЛЕНИЕ РАВНОДЕЙСТВУЮЩЕЙ АНАЛИТИЧЕСКИМ СПОСОБОМ Статика
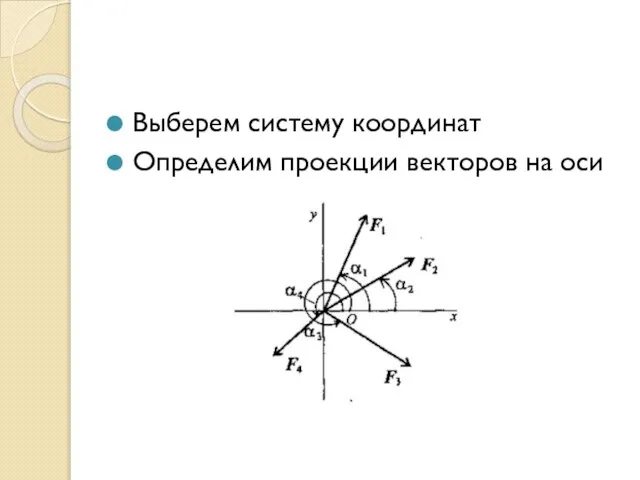
- 29. Выберем систему координат Определим проекции векторов на оси
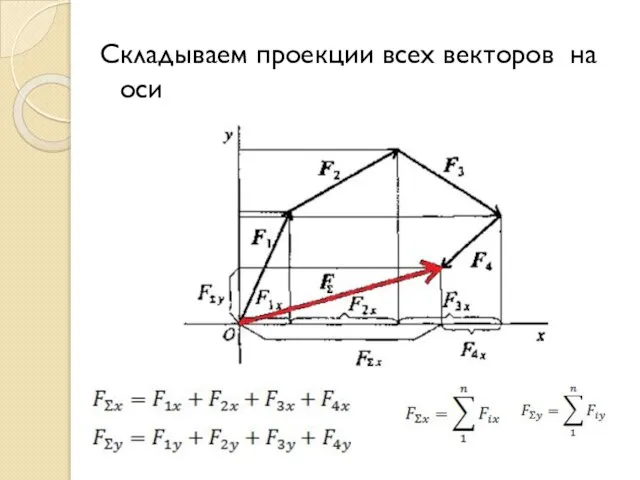
- 30. Складываем проекции всех векторов на оси
- 31. Модуль равнодействующей найдём по теореме Пифагора Направление равнодействующей − по величинам и знакам косинусов углов
- 32. Тело в равновесии ⇒ равнодействующая равна нулю
- 33. Условие равновесия в аналитической форме Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций
- 34. Задача 3 Определить величины и знаки проекций представленных сил
- 35. Задача 3 Определить величины и знаки проекций представленных сил
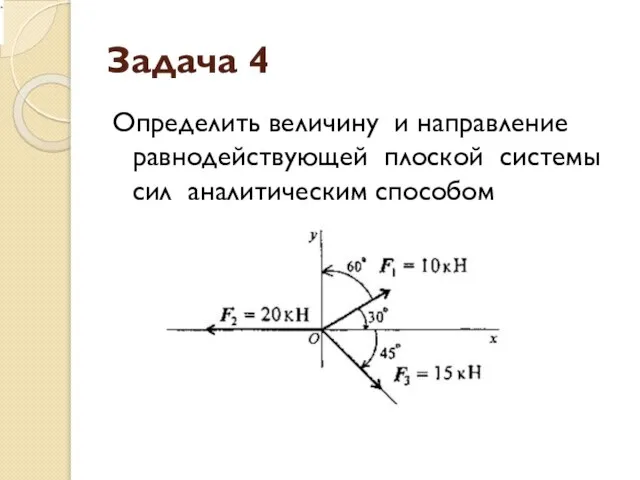
- 36. Задача 4 Определить величину и направление равнодействующей плоской системы сил аналитическим способом
- 37. Решение Проекции сил системы на ось Х Проекция равнодействующей на ось Х направлена влево
- 38. Проекции сил системы на ось Y Проекция равнодействующей на ось Y направлена вниз
- 39. Определяем модуль равнодействующей Определяем значение углов равнодействующей с осями
- 41. Скачать презентацию





















 Н. М. Карамзин и Симбирск
Н. М. Карамзин и Симбирск Федеральный государственный образовательный стандарт дошкольного образования от 17.10.2013 № 1155
Федеральный государственный образовательный стандарт дошкольного образования от 17.10.2013 № 1155 [Название]
[Название] Презентация на тему Образование в Японии
Презентация на тему Образование в Японии Междисциплинарная интеграция с использованием информационных технологий.
Междисциплинарная интеграция с использованием информационных технологий. МИФ или РЕАЛЬНОСТЬ?
МИФ или РЕАЛЬНОСТЬ? Исследователь и творец: какой он? ( 3 Межрегиональная конференция «Организация исследовательской деятельности детей и молодёжи: п
Исследователь и творец: какой он? ( 3 Межрегиональная конференция «Организация исследовательской деятельности детей и молодёжи: п Турция
Турция Нас ждет глобальное потепление! Льды растают и затопят низменные участки земли
Нас ждет глобальное потепление! Льды растают и затопят низменные участки земли Сказки М.Е. Салтыкова-Щедрина.
Сказки М.Е. Салтыкова-Щедрина. Умножение на 4
Умножение на 4 Загадка смерти Александра I
Загадка смерти Александра I Тушь Extreme Fashion
Тушь Extreme Fashion МАСТЕР-КЛАСС Критериально-ориентированное педагогическое тестирование Модуль № 2. Внутренняя экспертизатестов
МАСТЕР-КЛАСС Критериально-ориентированное педагогическое тестирование Модуль № 2. Внутренняя экспертизатестов Australian financial services consulting company (fintech)
Australian financial services consulting company (fintech) Афиши к спектаклю по драме А. Островского Гроза
Афиши к спектаклю по драме А. Островского Гроза Мастер - класс по нетрадиционным техникам рисования
Мастер - класс по нетрадиционным техникам рисования 1 сентября – День знаний
1 сентября – День знаний Физика и искусство
Физика и искусство Автомобильная промышленность
Автомобильная промышленность Арт менеджмент
Арт менеджмент  Бакалаврская работа. Анализ проектного финансирования как средства стимулирования экономического роста региона
Бакалаврская работа. Анализ проектного финансирования как средства стимулирования экономического роста региона Диагностика электоральной ситуации перед выборами в Государственную Думу РФПо заказу РЦОИТ при ЦИК РФ
Диагностика электоральной ситуации перед выборами в Государственную Думу РФПо заказу РЦОИТ при ЦИК РФ РОЛЬ КАРТОГРАФИИ В РАЗВИТИИ ОБЩЕСТВА
РОЛЬ КАРТОГРАФИИ В РАЗВИТИИ ОБЩЕСТВА о картофеле
о картофеле алфавит + звуки
алфавит + звуки Нарезание резьбы
Нарезание резьбы INFECTION CONTROL IN ICU
INFECTION CONTROL IN ICU