Внутренняя энергия газа

§§ Внутренняя энергия газа
02
В модели идеального газа силами
взаимодействия молекул пренебрегают
Внутренняя энергия газа равна сумме
энергий теплового движения молекул:
Внутренняя энергия не зависит от
способа перевода системы в данное
состояние
(функция состояния)

§§ Работа и теплота
03
Вычислим работу газа при расширении
p – давление газа
F = pS – сила, действующая
на поршень со стороны газа
элементарная работа
– работа газа при расширении
от V1 до V2

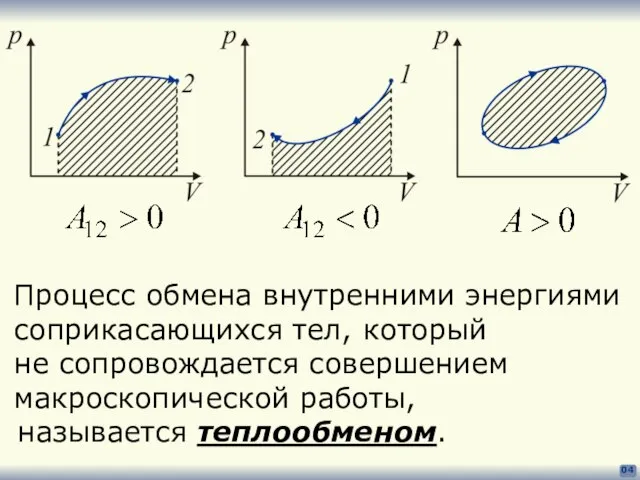
04
Процесс обмена внутренними энергиями
соприкасающихся тел,
который
не сопровождается совершением
макроскопической работы,
называется теплообменом.

§§ Первое начало
05
Термодинамическая система называется
изолированной,
если отсутствует
всякий обмен энергией между ней
и внешней средой
Для изолированной системы выполняется
закон сохранения и превращения
энергии
– полная энергия не изменяется
при любых процессах, происходящих
в этой системе.

06
Пусть системой α совершена
работа A, тогда
Рассмотрим контакт систем
в адиабатической оболочке.
неподвижная
теплопроводящая
перегородка
или
Обозначим
– убыль энергии системы β
(количество
теплоты, полученное системой α)

идет
на приращение ее внутренней энергии
ΔU = U2 – U1
07
Получаем математическую формулировку
I-го начала термодинамики
Теплота Q, полученная системой,
и совершение работы A

§§ Теплоемкость
08
Теплоемкость вещества –
физическая величина, равная
количеству теплоты,
необходимому
для нагревания вещества на 1 K
Различают теплоемкость вещества
при постоянном давлении Cp
и постоянном объеме CV.

09
Удельная теплоемкость:
Молярная теплоемкость:
Из первого начала
найдем молярную теплоемкость газа

10
1) V = const
2) p = const
рассмотрим уравнение М–К:

11
Для идеального газа справедливо
уравнение Майера
Для твердых тел и жидкостей Cp ≈ CV

§§ Изотермический процесс
12
Это бесконечно медленный процесс,
т.к. в системе должно установиться
термодинамическое равновесие
Закон Бойля–Мариотта:
Изменение внутренней энергии

13
1-е начало термодинамики
т.е. вся переданная рабочему телу
теплота идет на совершение телом
работы
Работа газа при изотермическом
расширении:

чтобы
не происходил обмен энергией
с окружающей средой или он был бы
несущественным
§§ Адиабатический процесс
(S = const, S – энтропия)
Это – очень быстрый процесс,
Уравнение Пуассона:
14
следовательно

15
1-е начало термодинамики
т.е. работа совершается за счет убыли
энергии системы
Работа газа при адиабатическом
процессе:

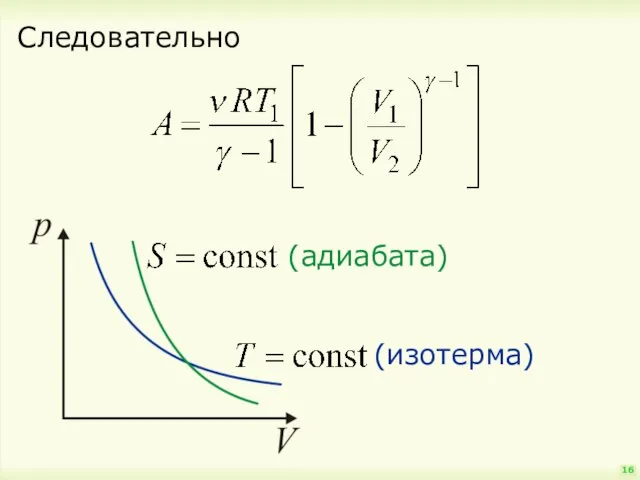
Следовательно
16

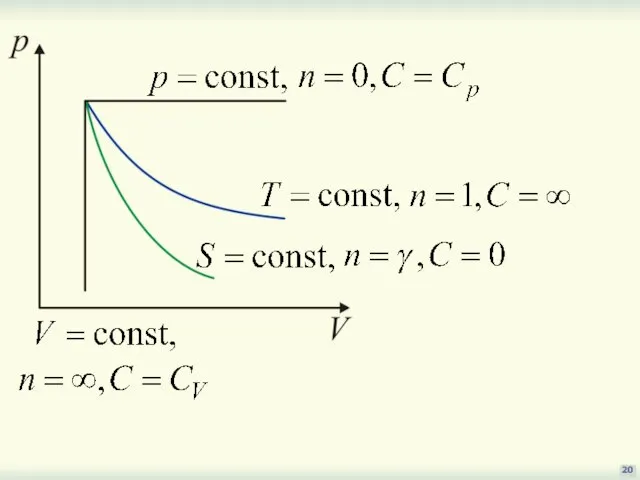
§§ Политропические процессы
17
Процесс, в котором теплоемкость
остается постоянной величиной,
называется политропическим
(политропным).
Рассмотренные процессы p,V,T,S = const
– частные случаи политропного процесса
Получим его общее уравнение:

18
сделаем замену R = Cp–CV и выразим dT

19
Интегрируя, получаем
или
– уравнение
политропы

20