Плоскость. Прямая и точка в плоскости. Прямые особого положения в плоскости (лекция 2)

Плоскость на чертеже может быть задана:
- проекциями трех точек, не лежащих на одной
прямой;
- проекциями прямой и точки,
не лежащей на ней;
- проекциями параллельных прямых;
- проекциями пересекающихся прямых;
- проекциями любой плоской фигуры;
- следами.
Способы задания плоскости
на чертеже

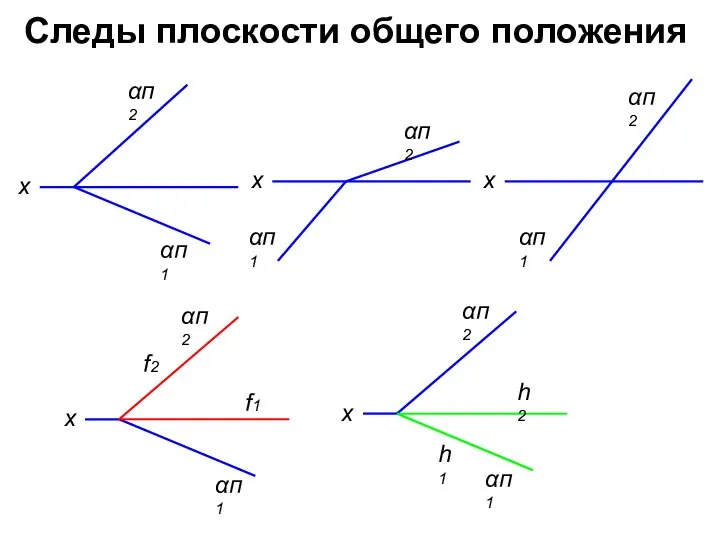
Следы плоскости общего положения
х
αп1
х
αп2
х
х
f1
f2
х
h1
h2
αп2
αп2
αп2
αп2
αп1
αп1
αп1
αп1

Классификация плоскостей
Плоскость относительно плоскостей проекций может занимать общее и частное положение. Плоскость общего положения – плоскость не параллельная и не перпендикулярная ни к одной из плоскостей проекций.
Плоскость общего положения может быть восходящей или нисходящей.

Плоскости частного положения
Проецирующие плоскости
- плоскости, перпендикулярные одной из плоскостей проекций.
1. Плоскость, ⊥ горизонтальной плоскости проекций, называется горизонтально проецирующей.
На горизонтальную плоскость проекций такая плоскость проецируется в прямую линию (проецирующий след).

2. Плоскость, ⊥ фронтальной плоскости проекций, называется
фронтально проецирующей.
На фронтальную плоскость проекций такая плоскость проецируется в прямую линию (проецирующий след).
3. Плоскость, ⊥ профильной плоскости проекций, называется
профильно проецирующей.
На профильную плоскость проекций такая плоскость проецируется в прямую линию (проецирующий след).

Плоскости уровня
плоскости, параллельные одной из плоскостей проекций. Все элементы, лежащие в этих плоскостях, на ту плоскость проекций, которой они параллельны,
проецируются в натуральную величину.
1. Плоскость, II горизонтальной плоскости проекций, называется горизонтальной уровня.

3. Плоскость, II профильной плоскости проекций, называется профильной уровня.
2. Плоскость, II фронтальной плоскости проекций, называется фронтальной уровня.

Условие принадлежности точки
и прямой линии плоскости
В пространстве прямая может либо принадлежать плоскости,
либо не принадлежать. Это утверждение справедливо и для точки.
Прямая принадлежит плоскости, если она проходит:
через две точки, принадлежащие плоскости;
через точку плоскости параллельно любой прямой этой плоскости.
Точка принадлежит плоскости, если она принадлежит любой прямой (кривой), лежащей в данной плоскости.