Подобные треугольники

Содержание

Пропорциональные отрезки

Подобные фигуры

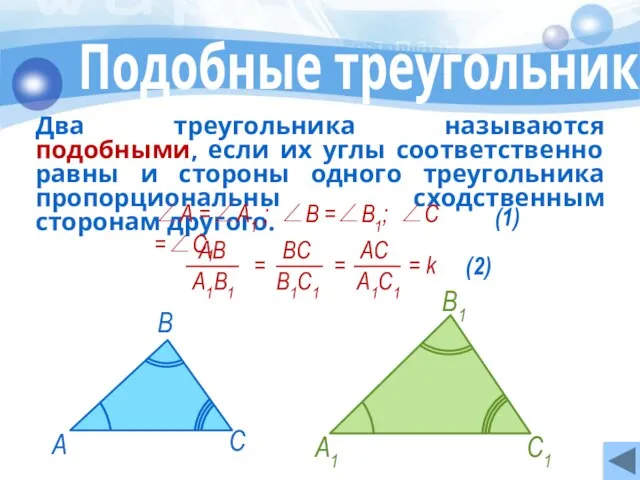
Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
∠А =∠А1 ; ∠В =∠В1; ∠С =∠С1
(1)
(2)

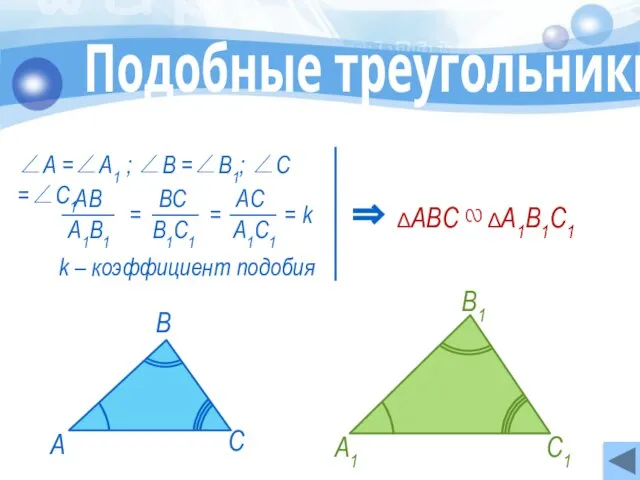
k – коэффициент подобия
∠А =∠А1 ; ∠В =∠В1; ∠С =∠С1
∆АВС ∾ ∆А1В1С1
⇒
Подобные треугольники

Т.к. ∠А =∠А1 , то по теореме об
k – коэффициент подобия
∆АВС ∾ ∆А1В1С1
⇒
Отношение площадей подобных треугольников
Дано:
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Теорема
Доказать:
Доказательство:
отношении площадей треугольников
По формуле (2)

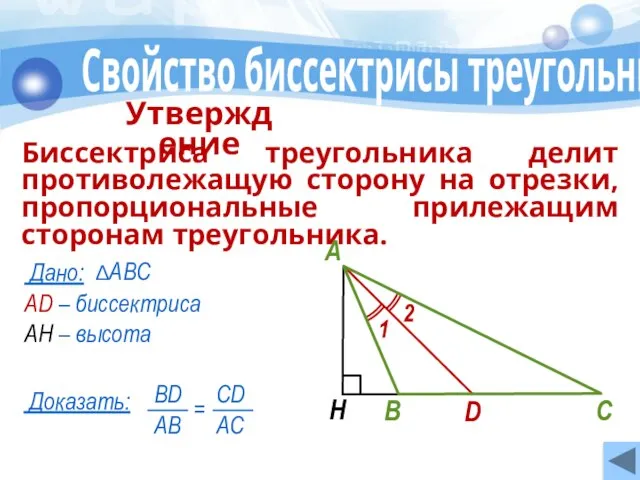
AD – биссектриса
АН – высота
∆АВС
Свойство биссектрисы треугольника
Дано:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Утверждение
Доказать:
Н
D
1
2

Т.к. ∆АВD и ∆АСD имеют общую высоту
⇒
Свойство биссектрисы треугольника
Доказательство:
углы (∠1 =∠2), поэтому
Из равенств (1) и (2) получаем
С другой стороны, эти же треугольники имеют равные
Ч.т.д.

Самостоятельная работа

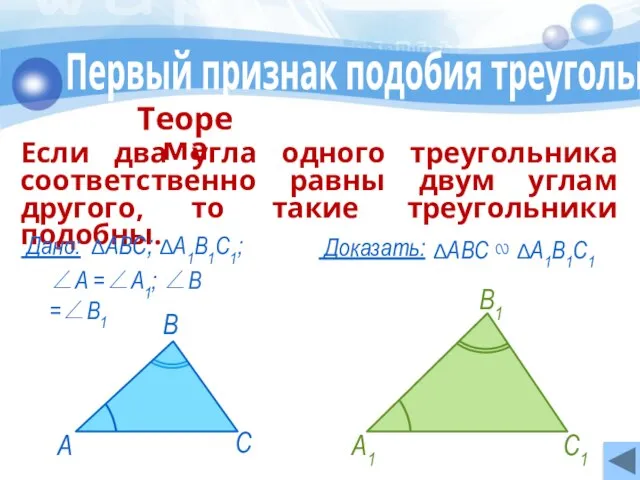
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Теорема
∆АВС ∾ ∆А1В1С1
Дано:
Доказать:
∠А =∠А1; ∠В =∠В1
∆АВС; ∆А1В1С1;

Первый признак подобия треугольников
Доказательство:
По теореме о сумме углов треугольника
Тогда по теореме об отношении площадей треугольников
С = 180° ‒ (∠А +∠В)
С1 = 180° ‒ (∠А1 +∠В1)
⇒ ∠С =∠С1
Таким образом, ∠А =∠А1 ; ∠В =∠В1; ∠С =∠С1.
из
⇒
Ч.т.д.

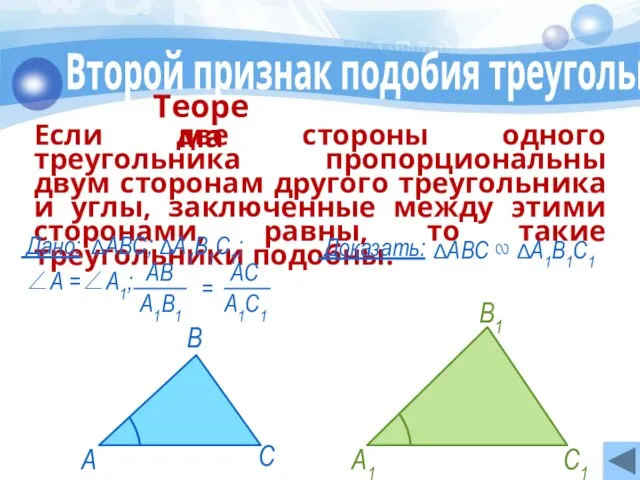
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Теорема
∆АВС ∾ ∆А1В1С1
Дано:
Доказать:
∠А =∠А1;
∆АВС; ∆А1В1С1;