Подструктуры математического мышления: как их выявить и использовать в преподавании

Актуальность
Математика – царица наук, пожалуй, самая точная и въедливая наука из всех. Ученые-психологи пришли к интересному выводу. В общей структуре мышления можно выделить пять типов математического мышления. Доминирующий тип и определяет мыслительную деятельность человека в разных практических случаях.
Для адаптации человека в обществе и полноценного функционирования в нем необходим высокий уровень общего развития. Математическое образование вносит свой вклад в формирование общей культуры человека. Одной из основных целей обучения математике является развитие мышления учащихся.
Данная работа открывает перед учащимися и учителями возможность оценить важность выявления доминирующей структуры мышления учеников, для развития индивидуальных способностей, подбора правильного курса обучения и помощи с освоением такой сложной, но интересной науки, как математика.

Цель исследования
Задачи
Методы исследования
Социологический

Историческая справка
Каждый выдающийся математик отличался собственным стилем творчества, проявлявшимся во многих произведениях.
Для Пифагора и его школы характерен мистико-математический стиль, т.е. изотерическое мировоззрение.
Для Демокрита был характерен математический атомизм, ставший первым предвестником дифференциального и интегрального исчислений.
Для Евклида - строго последовательный, предельно лаконичный.
Для Архимеда - гениальный своей простотой и смелостью механико-геометрический стиль доказательств

Основные подструктуры
математического мышления
Топологическое
Порядковое
Метрическое
Проективное
Алгебраическое

Топологическое мышление
Задачу сто раз «проверят», ошибок не допускают
Люди-топологи не любят действовать наобум
Склонны проделывать постоянные преобразования с объектом.
Им необходимо всегда начать действие с начала, не торопясь,
довести до конечного результата.

Порядковое мышление
Задачу решают
строго по алгоритму
«Порядковцы» любят строгий линейный порядок
В любых действиях стараются выработать алгоритм,
зависящий от какого-то объективного принципа.

Алгебраическое мышление
К решению каких-либо задач подходят с хаотическим настроем –
начинают с того места, которое им нравится
Алгебраистов сложно заставить делать что-то по правилам
Задачу решают быстро без объяснений, часто ошибаются

Задачу решают по действиям
Они всегда ясно представляют себе, что выйдет в результате работы
Метрическое мышление
Всегда и во всем они пытаются сводить к конкретным величинам
«Метристы» не любят образность и общность

Задачу решают самым неожиданным способом
Проективное мышление
Самый сложный тип из всех пяти
«Проективисты» склоны рассматривать предмет с разных точек зрения
Мыслят нестандартно, удивляют окружающих многовариантностью решений

B
D
A
F
C
O
1
2
3
4
5
Задача
Дано:
АВСDF – звезда
Найти:
‹1, ‹2, ‹3, ‹4, ‹5
B
D
A
F
C
O
1
2
3
4
5
1 Способ решения
Дополнительное построение
с применением теорем
о сумме внутренних углов треугольника
и о связи внешнего угла
треугольника
с его внутренними углами
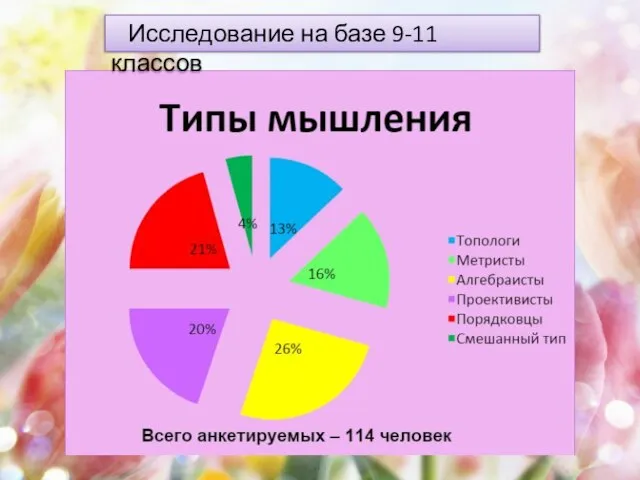
(свойственен людям с топологическим мышлением)
K
A
E
D
B
C
O₅
O₄
O₃
O₁
O₂
8
9
10
1
11
12
2
3
13
4
5
6
7
14
15
2 Способ решения
Традиционный способ
с применением теорем
о сумме углов треугольника,
свойстве внешнего угла и сумме внутренних углов пятиугольника
(свойственен людям с алгебраическим мышлением)
3 Способ решения
A
E
D
B
C
4
2
3
1
5
K
₎₎
₎
₎
₎₎
Способ с применением свойства внешнего угла треугольника, свойства вертикальных углов
N
(свойственен людям с порядковым мышлением)
A
E
D
B
C
4 Способ решения
Дополнительное построение с применением теоремы о сумме внутренних углов пятиугольника
(свойственен людям с метрическим мышлением)
F
N
G
M
H
5 Способ решения
A
E
D
B
C
4
2
3
1
5
K
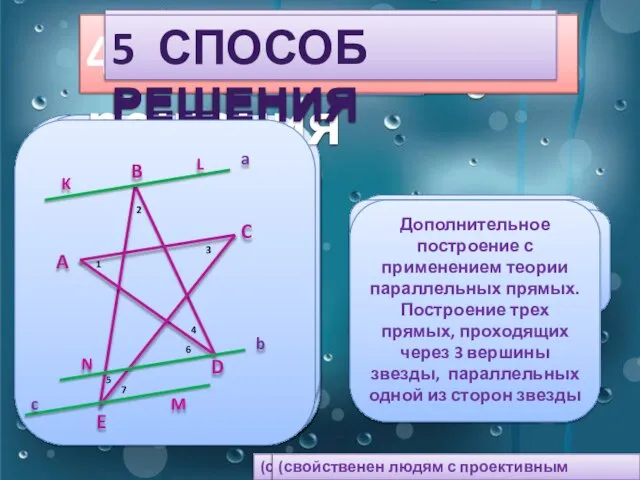
Дополнительное построение с применением теории параллельных прямых.
Построение трех прямых, проходящих через 3 вершины звезды, параллельных одной из сторон звезды
N
6
7
L
M
a
b
c
(свойственен людям с проективным мышлением)

Всего анкетируемых – 90 человек
Исследование на базе 2х и 5х классов

Исследование на базе 9-11 классов

Всего анкетируемых – 204 человек
Результирующая диаграмма

Наши рекомендации
Проводить входящее тестирование (1й класс; 5й класс;).
Чем раньше учитель узнает тип мышления ученика, тем проще потом будет строить процесс обучения, и благодаря этому, ребенку в будущем будет легче раскрыть свои способности, и он сможет легче усваивать учебный материал.
Не навязывать детям тот способ рассуждения, который свойствен самому учителю.
В этом случае дети, ведущая подструктура которых совпадает с
ведущей подструктурой педагога, легко его понимают, для них он понятно
и доступно объясняет. Для остальных же школьников усвоение
математики становится мукой.

Наши рекомендации
Проводить выходящие тесты (9й класс; 11й класс). Этот вид тестирования сможет помочь выпускникам подобрать правильный курс при подготовке к предстоящим экзаменам, а также, возможно, поможет определиться с выбором будущей профессии.
Не ломать математическую индивидуальность ученика, а учитывать ее и
строить процесс обучения в соответствии с ней – главная задача.
Зная математические особенности учеников,
учитель может учитывать их при составлении учебного плана, а также подбирать
задачи с несколькими вариантами решения.

В результате проделанной нами работы, мы добились реализации поставленных перед собой целей.
Во-первых, подробно изучили основные типы мышления.
Во-вторых, показали важность выявления доминирующей структуры мышления учеников.
В-третьих, показали важность выбора учителем правильного курса обучения математике.
В-четвертых, проведя собственное исследование, выявили доминирующие структуры математического мышления школьников младшего и старшего
звена.
Заключение

Спасибо за внимание!