Содержание
- 2. Цели урока: Рассмотреть осевую и центральную симметрии. Ввести понятие отображения плоскости на себя и движения.
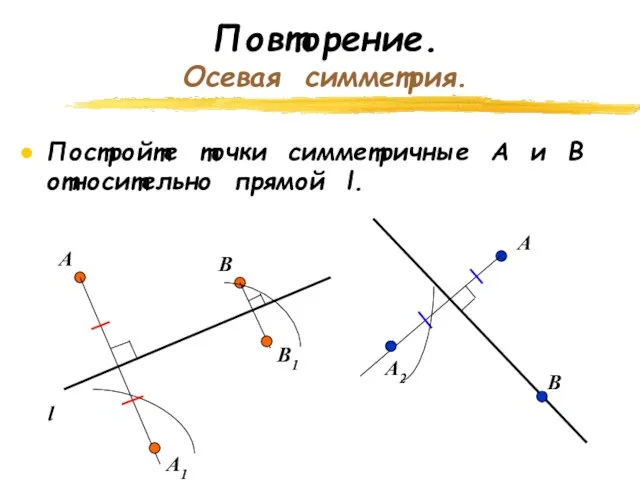
- 3. Повторение. Осевая симметрия. Постройте точки симметричные А и В относительно прямой l. l A В А1
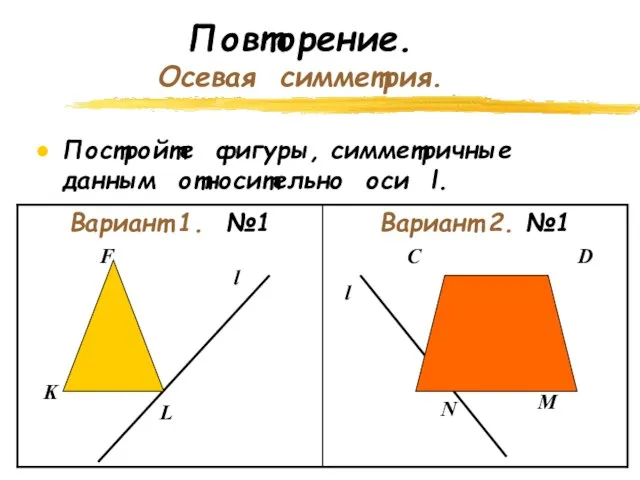
- 4. Повторение. Осевая симметрия. Постройте фигуры, симметричные данным относительно оси l. l F K L l C
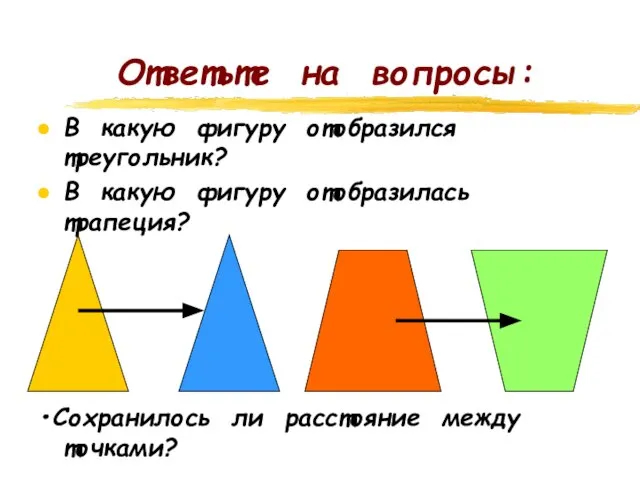
- 5. Ответьте на вопросы: В какую фигуру отобразился треугольник? В какую фигуру отобразилась трапеция? Сохранилось ли расстояние
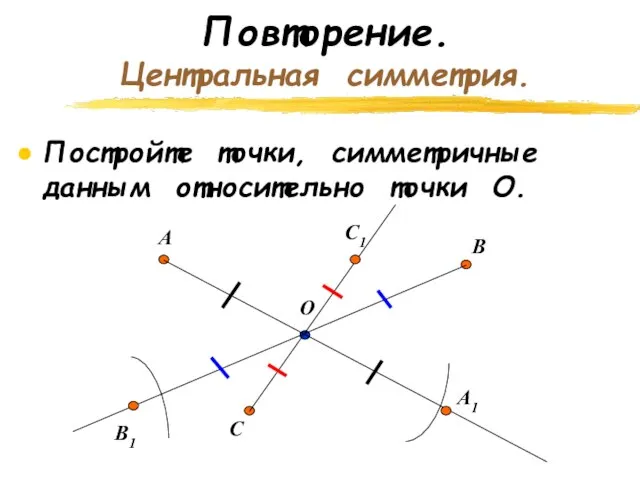
- 6. Повторение. Центральная симметрия. Постройте точки, симметричные данным относительно точки О. О А В С А1 В1
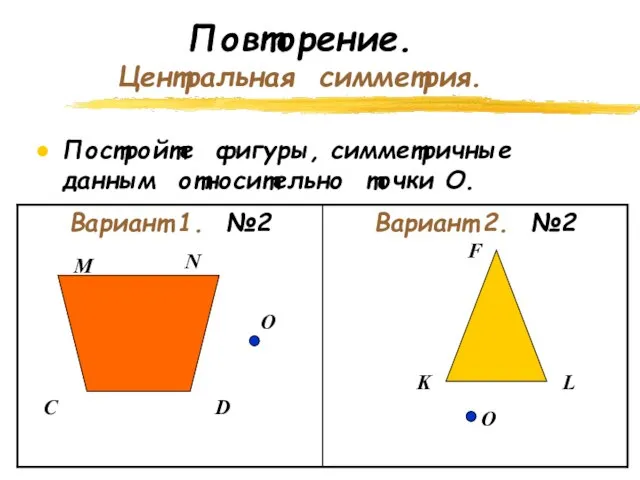
- 7. Повторение. Центральная симметрия. Постройте фигуры, симметричные данным относительно точки О. F K L C D N
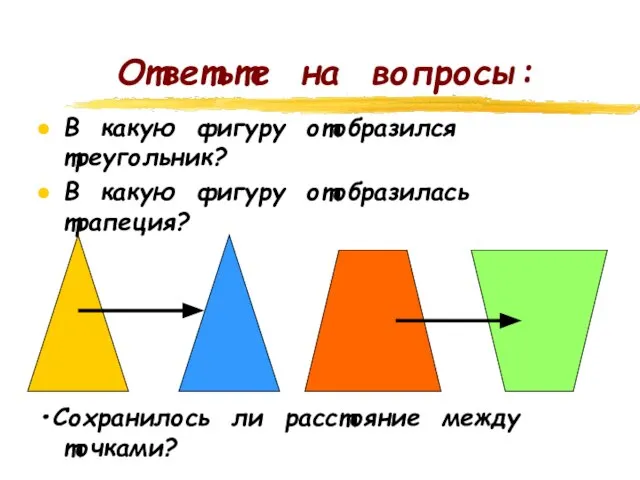
- 8. Ответьте на вопросы: В какую фигуру отобразился треугольник? В какую фигуру отобразилась трапеция? Сохранилось ли расстояние
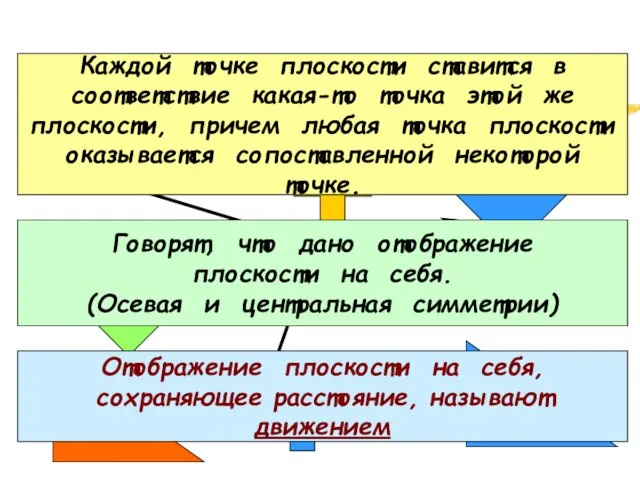
- 9. Найдите соответствия: Каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка
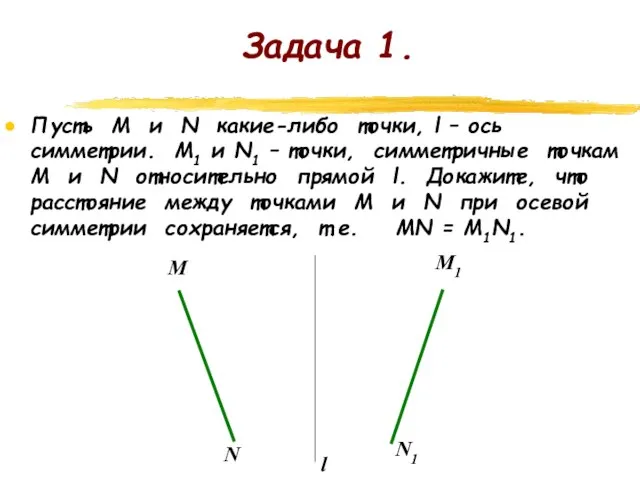
- 10. Задача 1. Пусть М и N какие-либо точки, l – ось симметрии. М1 и N1 –
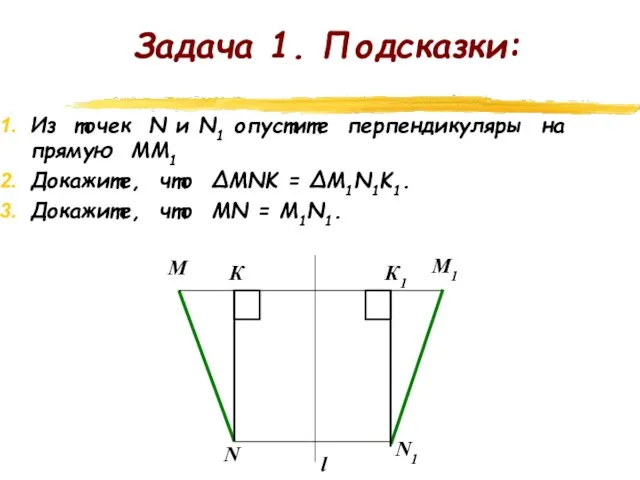
- 11. Задача 1. Подсказки: Из точек N и N1 опустите перпендикуляры на прямую ММ1 Докажите, что ∆MNK
- 12. Задача 2. (№3) Докажите, что центральная симметрия есть движение. Подсказки: Возьмите точки М и N и
- 14. Скачать презентацию

 Социальная стратификация и мобильность
Социальная стратификация и мобильность ФормЫ обращений в английском языке как компоненты эмоциональности речи
ФормЫ обращений в английском языке как компоненты эмоциональности речи Malsharuashylyq
Malsharuashylyq Диод КД103. Диод кремниевый диффузионный
Диод КД103. Диод кремниевый диффузионный ВЫЕЗДНОЕ ЗАСЕДАНИЕ СТУДЕНЧЕСКОГО СОВЕТА 16-18 октября 2009
ВЫЕЗДНОЕ ЗАСЕДАНИЕ СТУДЕНЧЕСКОГО СОВЕТА 16-18 октября 2009 Организационный менеджмент
Организационный менеджмент Банковская система. Функции банков
Банковская система. Функции банков Фразеологизмите
Фразеологизмите Шолохов
Шолохов Реформа электроэнергетики: Финишная прямая
Реформа электроэнергетики: Финишная прямая Микрофинансирование в банковском секторе РоссииБанк развития KfW
Микрофинансирование в банковском секторе РоссииБанк развития KfW Политические партии
Политические партии Основы конституционного строя России. Конституционный строй и его принципы
Основы конституционного строя России. Конституционный строй и его принципы Интеграционные процессы в Африке
Интеграционные процессы в Африке Процессоры фирмы Intel до Pentium III
Процессоры фирмы Intel до Pentium III Восточные единоборства
Восточные единоборства Игрушки Агния Барто
Игрушки Агния Барто Автомобилестроение, авиастроение. Легкая и мебельная промышленность
Автомобилестроение, авиастроение. Легкая и мебельная промышленность Team System - фреймворк для автоматизации тестирования от Microsoft
Team System - фреймворк для автоматизации тестирования от Microsoft МОДУЛЬ «БРОНИРОВАНИЕ»
МОДУЛЬ «БРОНИРОВАНИЕ»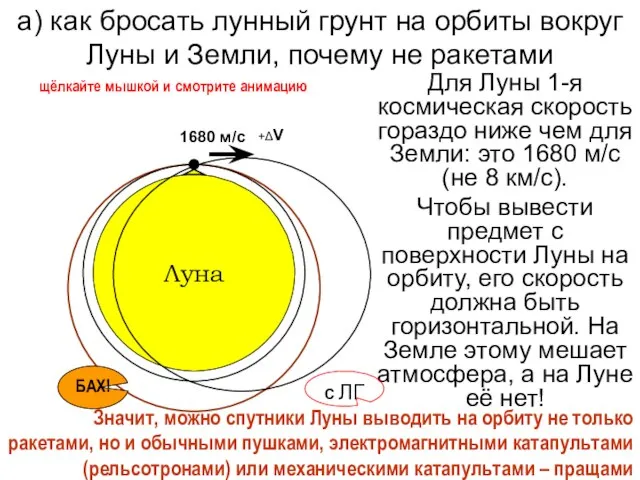 а) как бросать лунный грунт на орбиты вокруг Луны и Земли, почему не ракетами
а) как бросать лунный грунт на орбиты вокруг Луны и Земли, почему не ракетами О Т Ч Е То работе Управления записи актов гражданского состояния за 2004 год
О Т Ч Е То работе Управления записи актов гражданского состояния за 2004 год Українська мова. 4 клас
Українська мова. 4 клас PHIL 1- Lecture 3 - Week 3 moodle
PHIL 1- Lecture 3 - Week 3 moodle Эвены
Эвены Что такое предпринимательство и бизнес + конспект
Что такое предпринимательство и бизнес + конспект © МОУ СОШ №6, г.Тутаев, 2006
© МОУ СОШ №6, г.Тутаев, 2006 ТЕАТР XIX ВЕКА Западноевропейский театр романтизма и реализма Русский театр романтизма и реализма
ТЕАТР XIX ВЕКА Западноевропейский театр романтизма и реализма Русский театр романтизма и реализма