Содержание
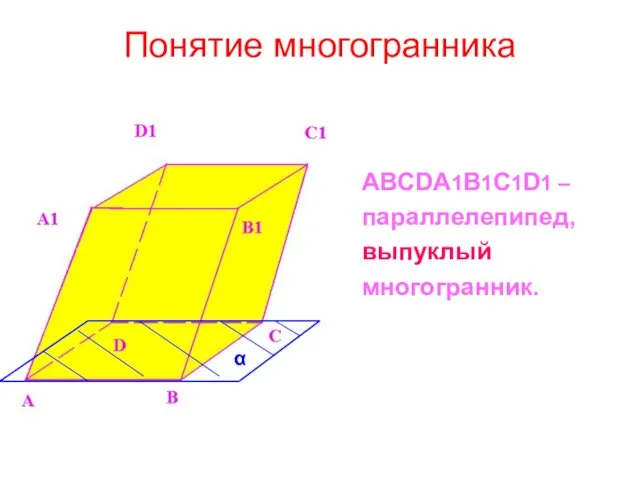
- 2. Понятие многогранника ABCDA1B1C1D1 – параллелепипед, выпуклый многогранник. α
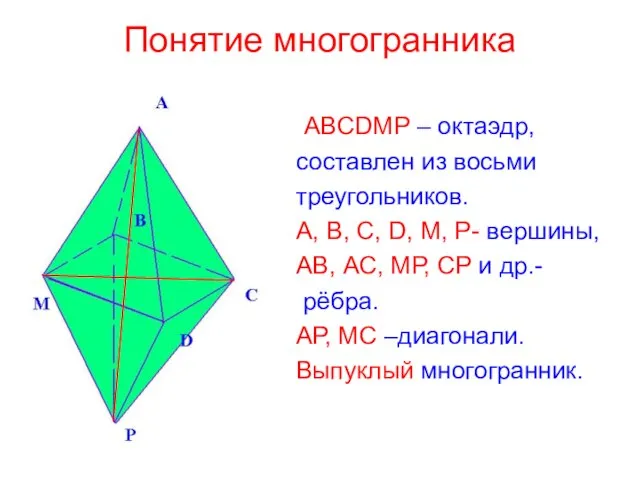
- 3. Понятие многогранника ABCDMP – октаэдр, составлен из восьми треугольников. A, B, C, D, M, P- вершины,
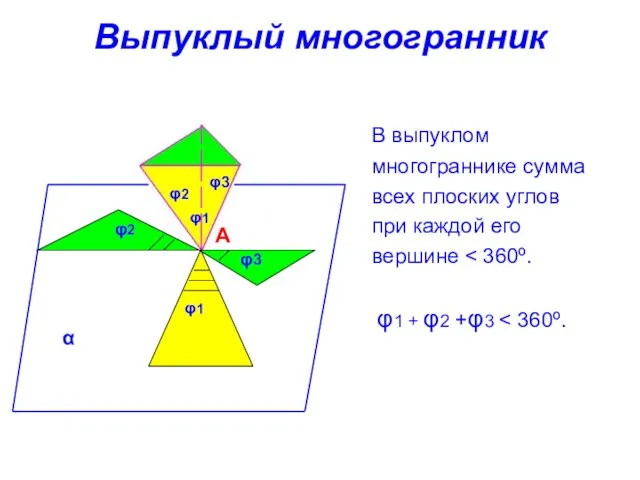
- 4. Выпуклый многогранник В выпуклом многограннике сумма всех плоских углов при каждой его вершине φ1 + φ2
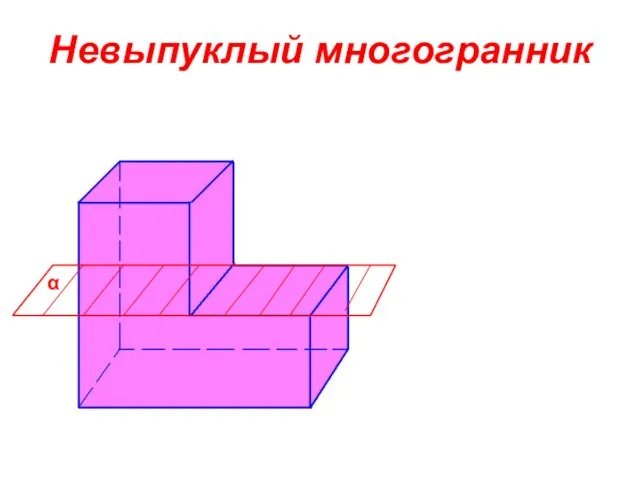
- 5. Невыпуклый многогранник α
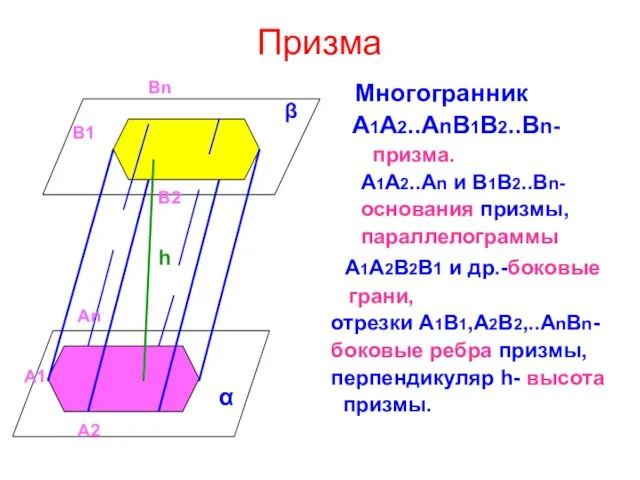
- 6. Призма Многогранник А1А2..АnB1B2..Bn- призма. А1А2..Аn и В1В2..Вn- основания призмы, параллелограммы А1А2В2В1 и др.-боковые грани, отрезки А1В1,А2В2,..АnВn-
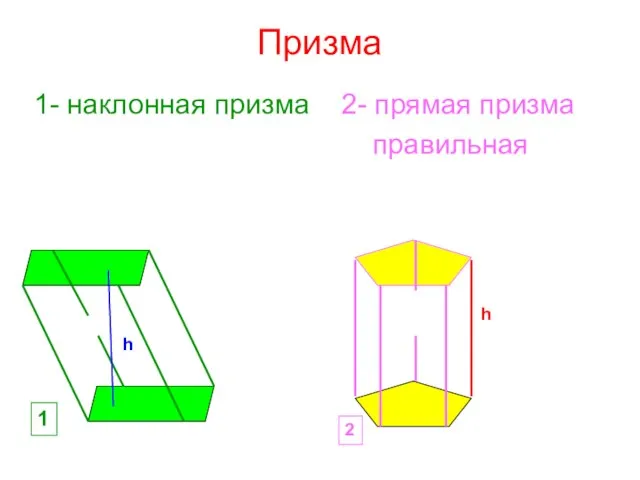
- 7. Призма 1- наклонная призма 2- прямая призма правильная 1 2 h h
- 8. Евклид определяет призму как телесную фигуру, заключенную между двумя равными и параллельными плоскостями (основаниями) и с
- 9. Дисперсия света
- 10. Дисперсия света В 60-х годах ХVII столетия Исаак Ньютон проводил эксперименты со светом. Чтобы разложить свет
- 11. Исаак Ньютон 1642 —1727
- 12. Применение призм Оптика, медицина, электронная техника. 1- очки 2- бинокли 3- объективы 4- телефоны 1 2
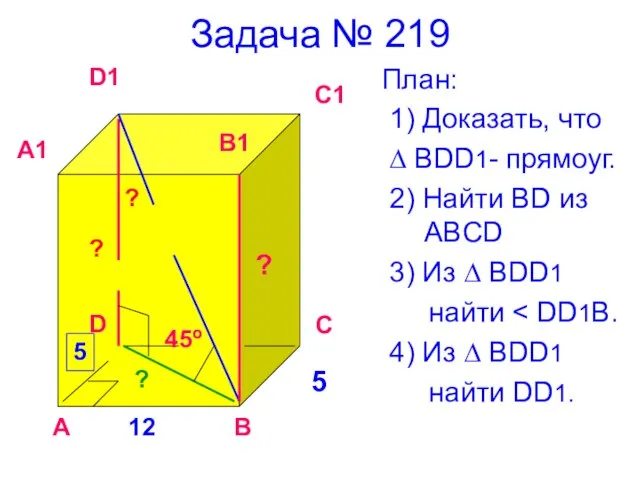
- 13. Задача № 219 План: 1) Доказать, что ∆ BDD1- прямоуг. 2) Найти BD из ABCD 3)
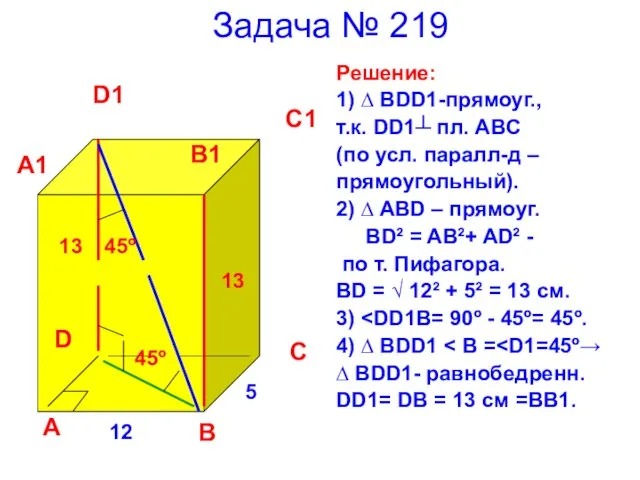
- 14. Задача № 219 Решение: 1) ∆ BDD1-прямоуг., т.к. DD1┴ пл. ABC (по усл. паралл-д – прямоугольный).
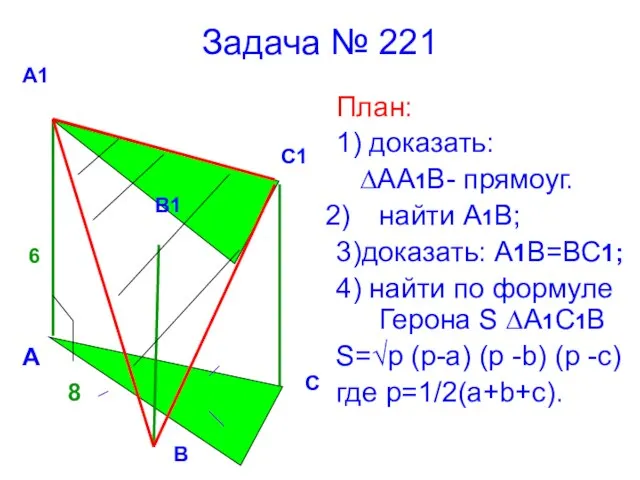
- 15. Задача № 221 План: 1) доказать: ∆АА1В- прямоуг. найти А1В; 3)доказать: А1В=ВС1; 4) найти по формуле
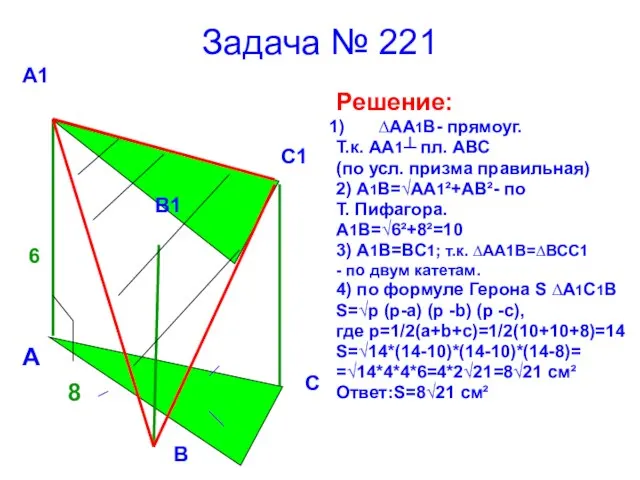
- 16. Задача № 221 Решение: ∆АА1В- прямоуг. Т.к. АА1┴ пл. АВС (по усл. призма правильная) 2) А1В=√АА1²+АВ²-
- 17. Вопросы Дайте определение многогранника. Приведите примеры многогранников. Какие многогранники называют выпуклыми (невыпуклыми)? 4) Какой многогранник называют
- 19. Скачать презентацию






 ПЕДАГОГИКА ПОДДЕРЖКИ РЕБЕНКА И ПРОЦЕСС ЕГО РАЗВИТИЯ В СИСТЕМЕ ЛИЧНОСТНО-ОРИЕНТИРОВАННОГО ВОСПИТАНИЯ
ПЕДАГОГИКА ПОДДЕРЖКИ РЕБЕНКА И ПРОЦЕСС ЕГО РАЗВИТИЯ В СИСТЕМЕ ЛИЧНОСТНО-ОРИЕНТИРОВАННОГО ВОСПИТАНИЯ Лас су желісі. Канализация құбырлары мен коллекторларының кесінді қималары
Лас су желісі. Канализация құбырлары мен коллекторларының кесінді қималары Career in law abroad
Career in law abroad  ТЕМА : ГЛАГОЛ
ТЕМА : ГЛАГОЛ Технология обработки сырья и приготовления блюд
Технология обработки сырья и приготовления блюд Prezentare (2)
Prezentare (2)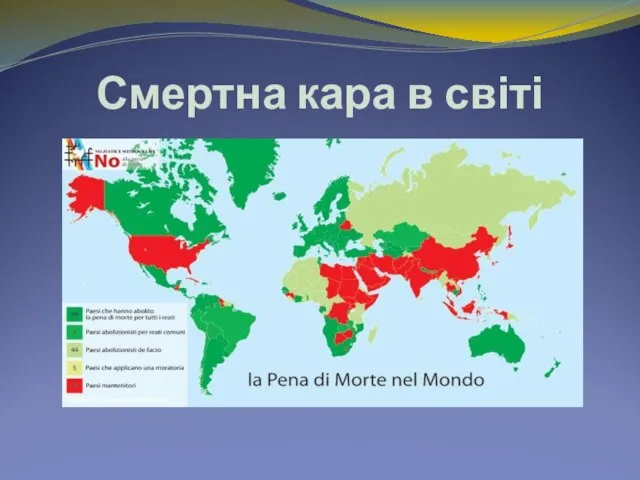 Смертная карта
Смертная карта  Центр независимых судебных экспертиз ТЕХЭКО
Центр независимых судебных экспертиз ТЕХЭКО Изложение Птицы говорят спасибо
Изложение Птицы говорят спасибо Классификация стиральных порошков
Классификация стиральных порошков Утомление при физической и умственной работе восстановление
Утомление при физической и умственной работе восстановление Презентация на тему МАТЕМАТИКА 1 КЛАСС
Презентация на тему МАТЕМАТИКА 1 КЛАСС  Презентация на тему Загадочная Намибия Племя Химба
Презентация на тему Загадочная Намибия Племя Химба  Слайд 1
Слайд 1 Правила делового этикета: как не ударить в грязь лицом
Правила делового этикета: как не ударить в грязь лицом Проект воздухоразделительной установки №7 в условиях АО Уральская Сталь
Проект воздухоразделительной установки №7 в условиях АО Уральская Сталь «Рио+20», устойчивое развитие и торговля
«Рио+20», устойчивое развитие и торговля Поэтам и писателям. Нургисаева Айжана
Поэтам и писателям. Нургисаева Айжана Проверка парных согласных и безударных гласных в корне слова
Проверка парных согласных и безударных гласных в корне слова Картины художников-передвижников
Картины художников-передвижников Информационные системы
Информационные системы Проведение сертификационных испытаний на отсутствие НДВ. Можно ли найти НДВ?
Проведение сертификационных испытаний на отсутствие НДВ. Можно ли найти НДВ? Инфекция мочевыводящих путей у беременных
Инфекция мочевыводящих путей у беременных Политический режим
Политический режим Московский Городской Педагогический УниверситетФакультет специальной педагогики
Московский Городской Педагогический УниверситетФакультет специальной педагогики Базиликовый соус Суго
Базиликовый соус Суго Семинар заместителей директоров по учебно-воспитательной работе:
Семинар заместителей директоров по учебно-воспитательной работе: История школьного портфеля
История школьного портфеля