Понятие объема многогранников. Объем прямоугольного параллелепипеда

1. О понятие объема тела
Аналогия с S M S(M)
Равные многоугольники имеют равные площади.
Площадь многоугольника равна сумме площадей составляющих его многоугольников, если они не имеют общих точек.
Площадь единичного квадрата равна единице.

e
e – единица длины
е
Единичный квадрат
Пользуясь наличием единичного квадрата , площадь S любого многоугольника можно представить в виде S = se² , где s – количество «укладываемых» в многоугольник единичных квадратов.

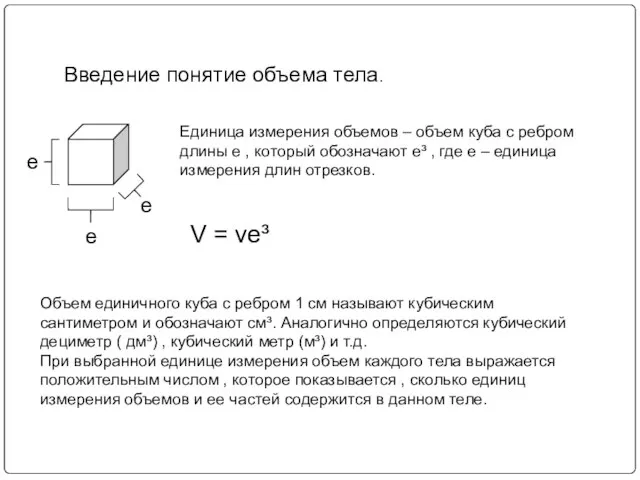
Введение понятие объема тела.
е
е
е
Единица измерения объемов – объем куба с ребром длины е , который обозначают е³ , где е – единица измерения длин отрезков.
V = ve³
Объем единичного куба с ребром 1 см называют кубическим сантиметром и обозначают см³. Аналогично определяются кубический дециметр ( дм³) , кубический метр (м³) и т.д.
При выбранной единице измерения объем каждого тела выражается положительным числом , которое показывается , сколько единиц измерения объемов и ее частей содержится в данном теле.

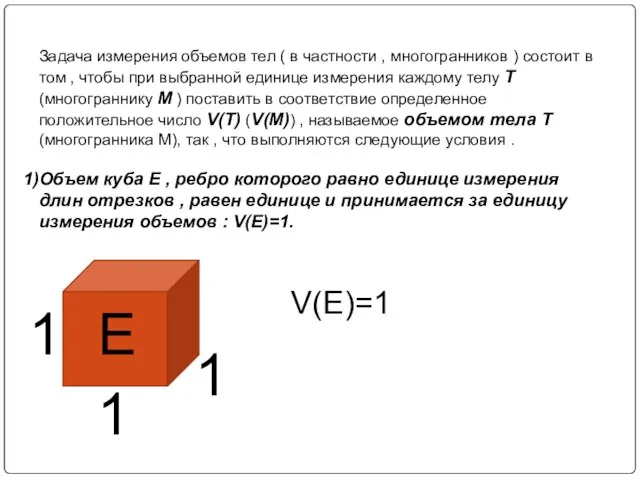
Задача измерения объемов тел ( в частности , многогранников ) состоит в том , чтобы при выбранной единице измерения каждому телу Т (многограннику М ) поставить в соответствие определенное положительное число V(T) (V(M)) , называемое объемом тела Т (многогранника М), так , что выполняются следующие условия .
Объем куба Е , ребро которого равно единице измерения длин отрезков , равен единице и принимается за единицу измерения объемов : V(E)=1.
1
1
1
Е
V(E)=1

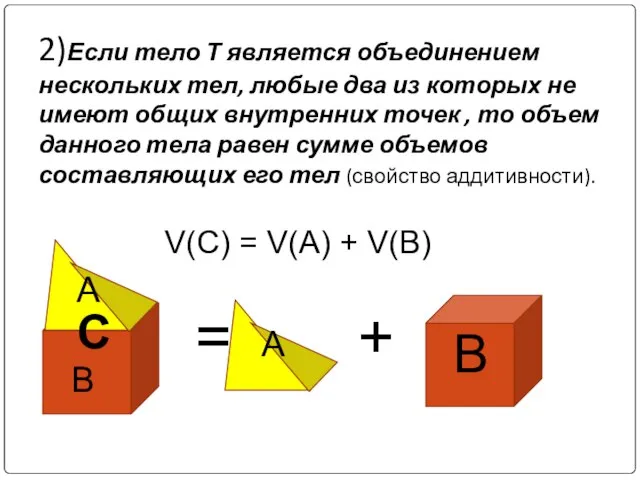
2)Если тело Т является объединением нескольких тел, любые два из которых не имеют общих внутренних точек , то объем данного тела равен сумме объемов составляющих его тел (свойство аддитивности).
=
+
V(C) = V(A) + V(B)
B
B
A
A
C

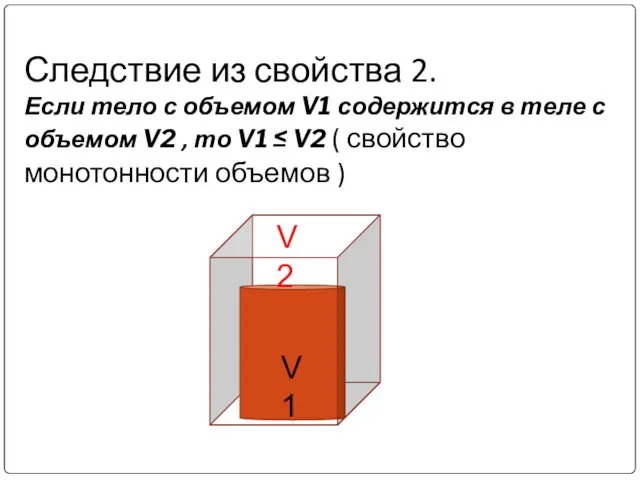
Следствие из свойства 2.
Если тело с объемом V1 содержится в теле с объемом V2 , то V1 ≤ V2 ( свойство монотонности объемов )
V1
V2

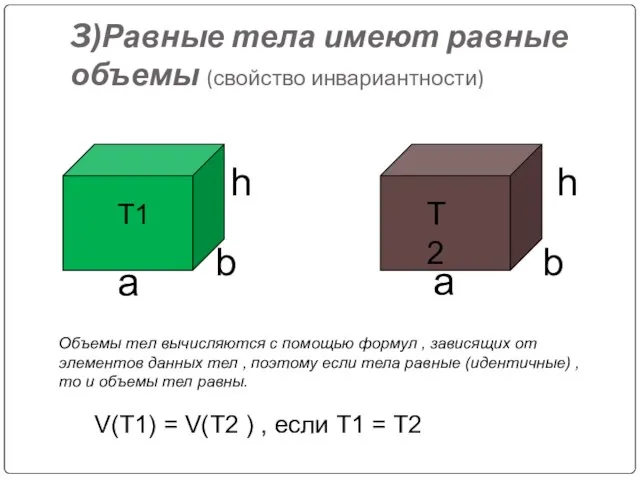
3)Равные тела имеют равные объемы (свойство инвариантности)
Объемы тел вычисляются с помощью формул , зависящих от элементов данных тел , поэтому если тела равные (идентичные) , то и объемы тел равны.
a
a
b
b
h
h
T1
T2
V(T1) = V(T2 ) , если Т1 = Т2

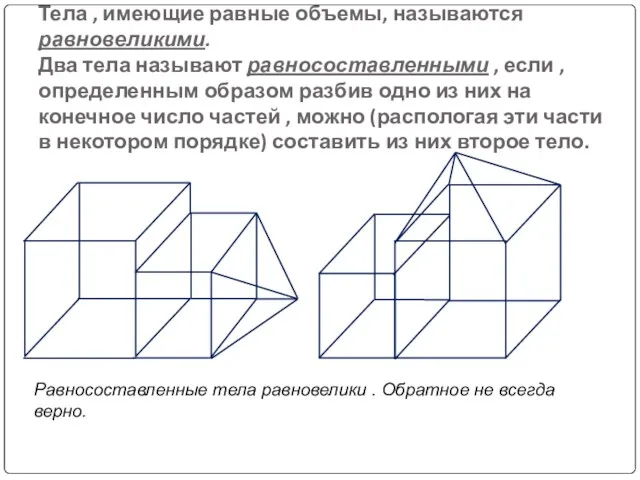
Тела , имеющие равные объемы, называются равновеликими.
Два тела называют равносоставленными , если , определенным образом разбив одно из них на конечное число частей , можно (распологая эти части в некотором порядке) составить из них второе тело.
Равносоставленные тела равновелики . Обратное не всегда верно.

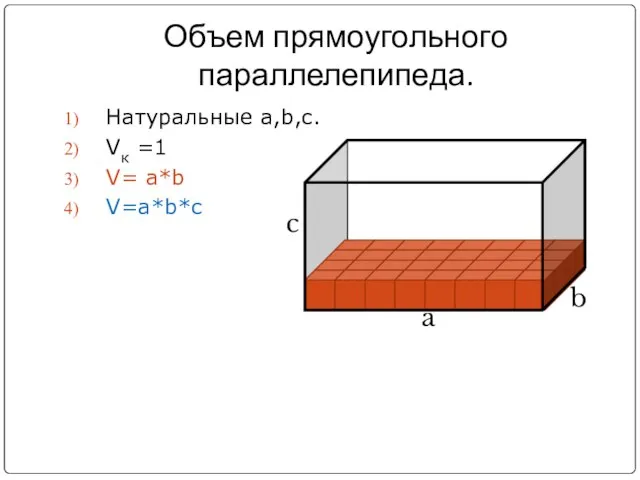
Объем прямоугольного параллелепипеда.
Натуральные a,b,c.
Vк =1
V= a*b
V=a*b*c
a
b
c

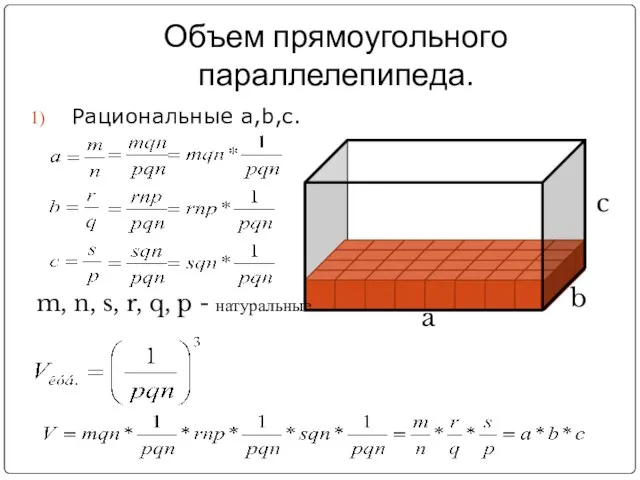
Объем прямоугольного параллелепипеда.
Рациональные a,b,c.
m, n, s, r, q, p - натуральные
a
b
c