Слайд 5I. Что можно надежно утверждать об экспрессии генов?
Резко выраженная дифференциальная экспрессия.
Мы видели,

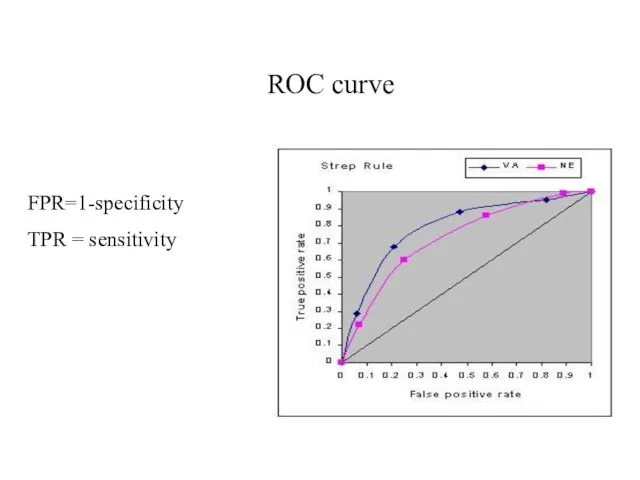
что после нормализации и сложной обработки можно достаточно надежно заметить, что экспрессия изменилась в 2 и более раза. Это значит, что можно строить синдромы типа: 1, если Eg>a, 0, если Eg 2b.
2. Утверждения об экспрессии, не требующие нормализации.
Монотонно возрастающие функции.
A) Модель, не учитывающая неспецифической гибридизации
Интенсивность j-ого зонда гена g на k-том чипе
I(g, j, k) = Сk(f(j)E(g)), где Сk() – монотонное нелинейное влияние k-ого чипа,
f(j) – эффективность j-ого зонда, E(g) – экспрессия гена g.
Из монотонности следует, что I(g1, j1, k) > I(g2, j2,k) ⬄ E(g1)/E(g2) > f(j2)/f(j1)
Важно, что f(j2) и f(j1) не меняются от чипа к чипу. Поэтому, если I(g1, j1, k) >I(g2, j2,k) выполняется часто на одном классе и редко на другом, то это хороший симптом.







 Локальная фармацевтическая промышленность: возможности импортозамещения
Локальная фармацевтическая промышленность: возможности импортозамещения Исследовательская работа по литературе.
Исследовательская работа по литературе. 10 А класс МОУ СОШ №154 Учитель: Колоскова Людмила Леонтьевна
10 А класс МОУ СОШ №154 Учитель: Колоскова Людмила Леонтьевна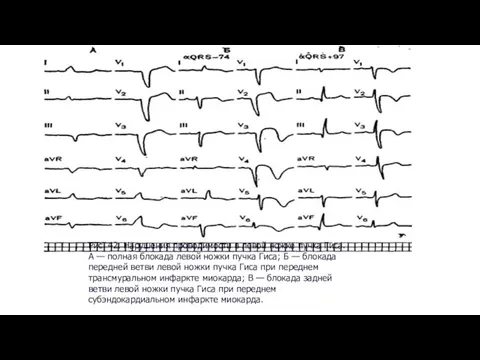 Нарушения проводимости в левой ножке пучка
Нарушения проводимости в левой ножке пучка Световые явления вокруг нас
Световые явления вокруг нас Обучение написанию сочинения на лингвистическую тему
Обучение написанию сочинения на лингвистическую тему Мучные изделия
Мучные изделия Презентация на тему Инфекционные болезни
Презентация на тему Инфекционные болезни  Навігація
Навігація Тема 4 .2 10 класс
Тема 4 .2 10 класс Презентация на тему Подготовка к ЕГЭ по математике
Презентация на тему Подготовка к ЕГЭ по математике  Программа курса«Литературное наследие Сибири»
Программа курса«Литературное наследие Сибири» Формирование психологической зависимости от ролевых компьютерных игр.
Формирование психологической зависимости от ролевых компьютерных игр. 23 февраля
23 февраля Образ России в творчестве поэтов Любимского края
Образ России в творчестве поэтов Любимского края Словацко-российские стипендии на обучение для студентов, аспирантов, научно-педагогических работников
Словацко-российские стипендии на обучение для студентов, аспирантов, научно-педагогических работников Любимый край . Обзор рынка
Любимый край . Обзор рынка Стандарт BRC S&D. Хранение и транспортировка пищевой продукции
Стандарт BRC S&D. Хранение и транспортировка пищевой продукции Медиаобразование как средство формирования коммуникативной образовательной среды гимназии № 18 г. Нижнего Тагила
Медиаобразование как средство формирования коммуникативной образовательной среды гимназии № 18 г. Нижнего Тагила Мифологические ПТИЦЫ славян
Мифологические ПТИЦЫ славян Развивающая игра Чего не хватает?
Развивающая игра Чего не хватает? Бортовой комплекс обороны вертолета Ми-28Н
Бортовой комплекс обороны вертолета Ми-28Н Прикладная композиция
Прикладная композиция История хлеба
История хлеба Система управления и методы регулирования рынка транспортных услуг
Система управления и методы регулирования рынка транспортных услуг 01_11_Pravookhran_i_sud_organy_Makeev_lek_40_02_03_FNO_och_1_k__1_-1
01_11_Pravookhran_i_sud_organy_Makeev_lek_40_02_03_FNO_och_1_k__1_-1 Основные шаги в русском танце
Основные шаги в русском танце Красота родной природы пейзаж в графике
Красота родной природы пейзаж в графике