Содержание
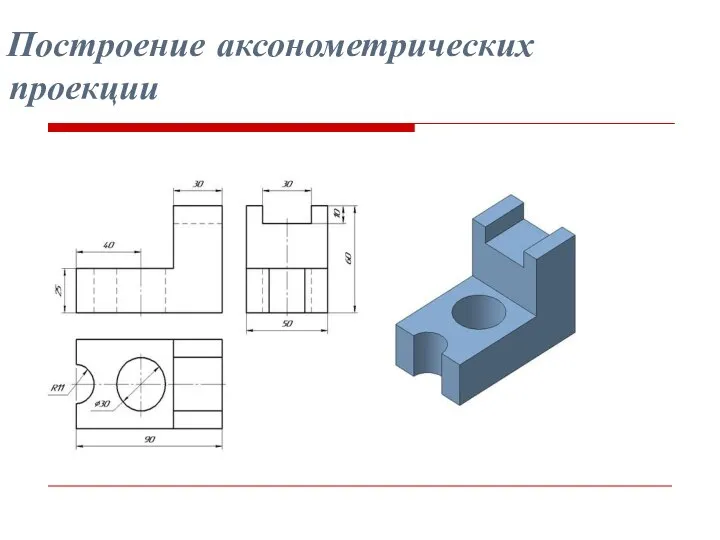
- 2. Построение аксонометрических проекции
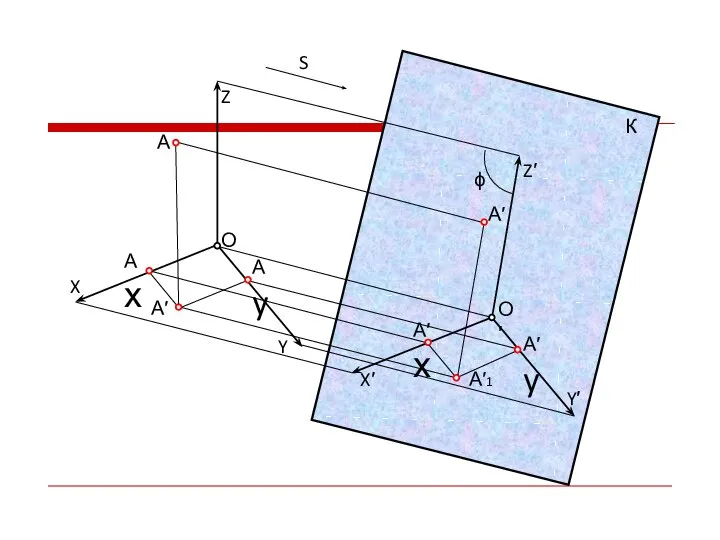
- 4. Понятие “Аксонометрия” образовано из слов древнегреческого языка: “аксон”- ось и “метрео”- измеряю - измерение по осям.
- 5. О Ах Аy А′ А′1 Z Y X ϕ S X′ Z′ Y′ А′х А′y А
- 6. СТАНДАРТНЫЕ АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ Прямоугольные – направление проецирования перпендикулярно плоскости чертежа изометрия диметрия Косоугольные фронтальная изометрия горизонтальная
- 7. коэффициенты искажения аксонометрических проекций – отношение аксонометрических проекций отрезков к их натуральным величинам - Изометрия –
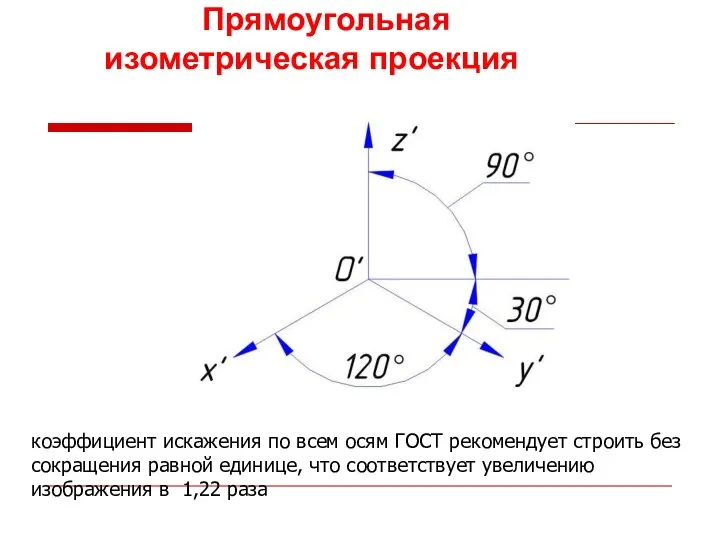
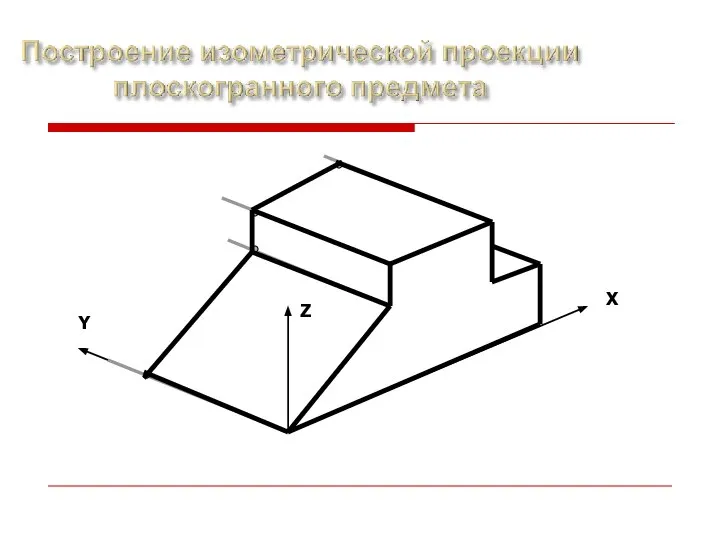
- 8. Прямоугольная изометрия
- 9. Прямоугольная изометрическая проекция коэффициент искажения по всем осям ГОСТ рекомендует строить без сокращения равной единице, что
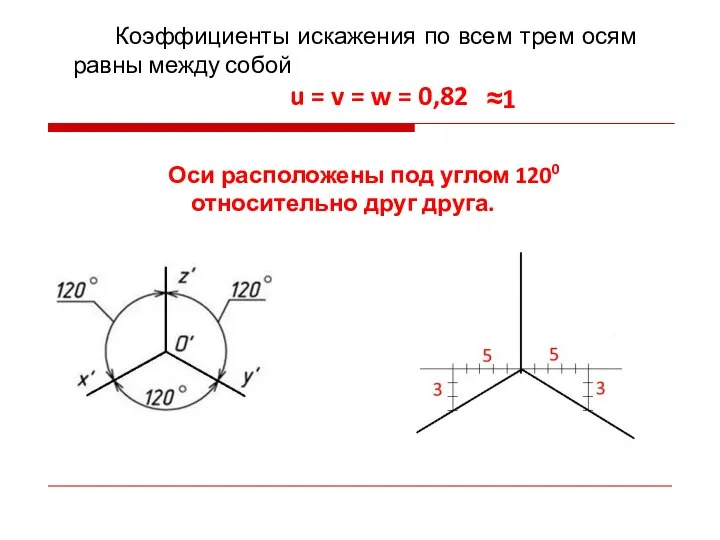
- 10. Коэффициенты искажения по всем трем осям равны между собой u = v = w = 0,82
- 11. Z X Y
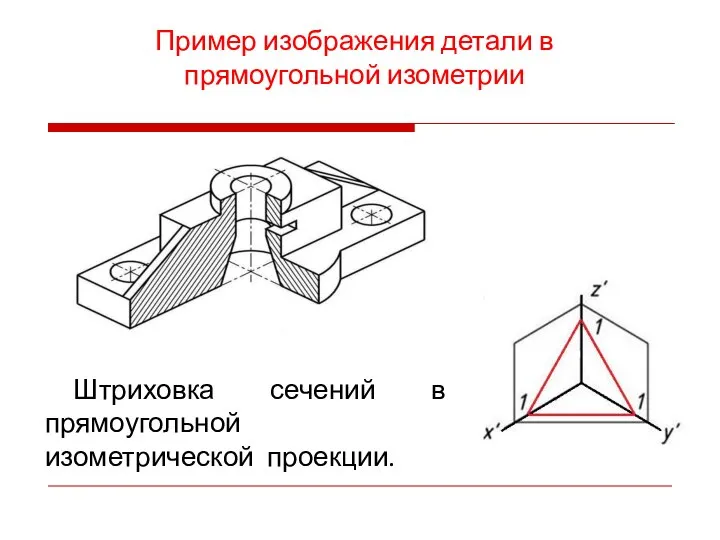
- 12. Пример изображения детали в прямоугольной изометрии Штриховка сечений в прямоугольной изометрической проекции.
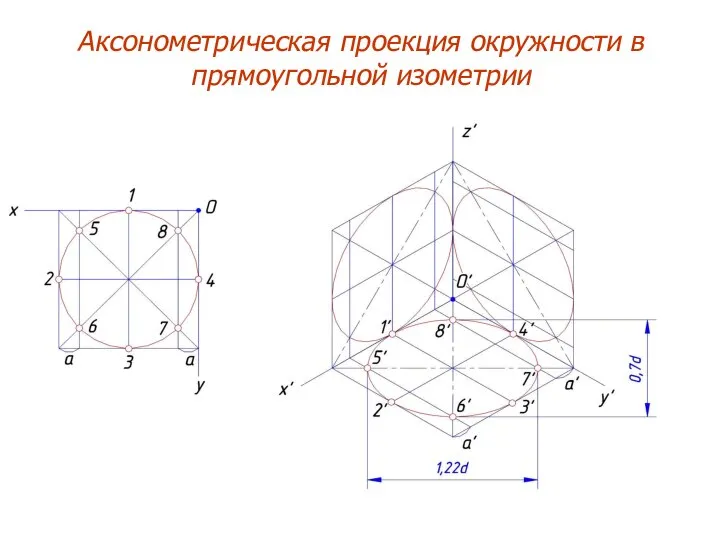
- 13. Аксонометрическая проекция окружности в прямоугольной изометрии
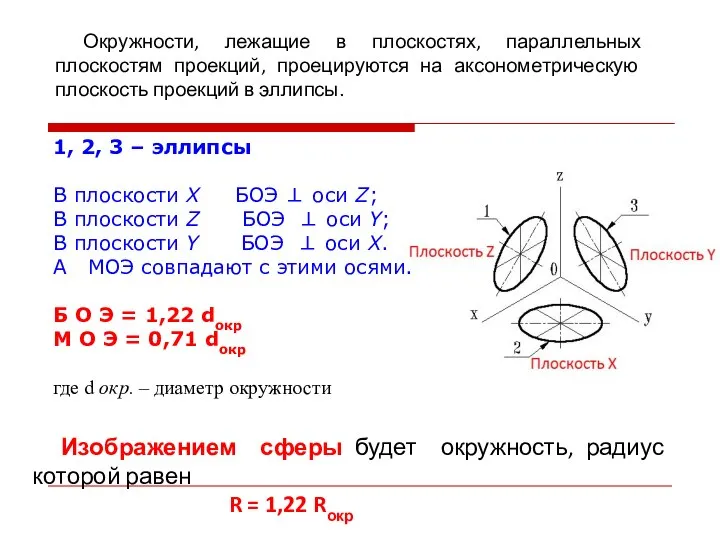
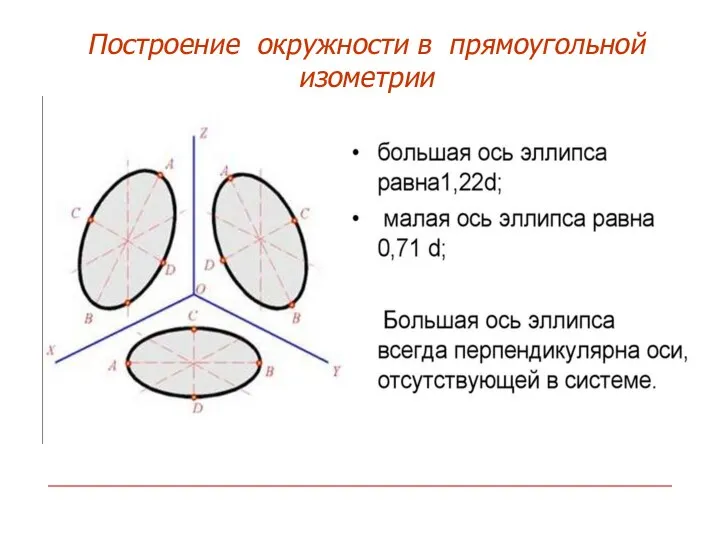
- 14. 1, 2, 3 – эллипсы В плоскости Х БОЭ ⊥ оси Z; В плоскости Z БОЭ
- 15. Построение окружности в прямоугольной изометрии
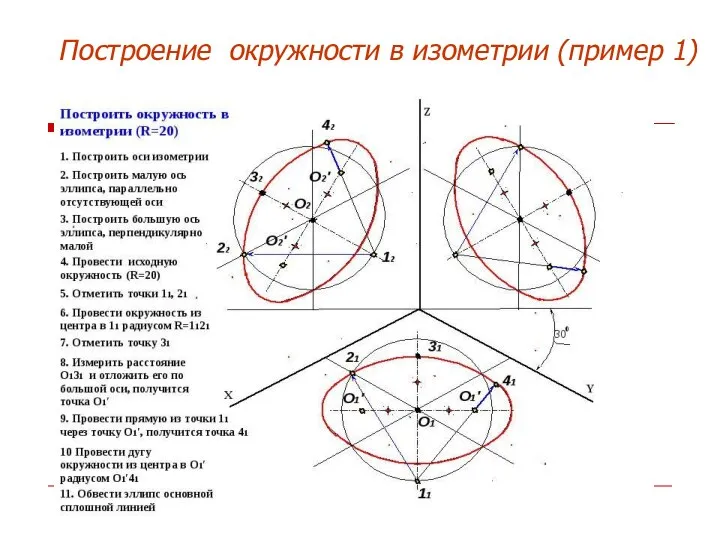
- 16. Построение окружности в изометрии (пример 1)
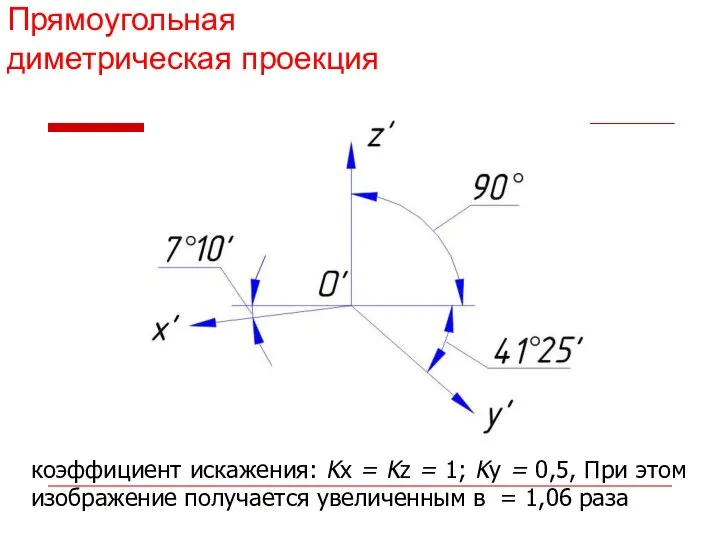
- 17. Прямоугольная диметрия
- 18. Прямоугольная диметрическая проекция коэффициент искажения: Kx = Kz = 1; Ky = 0,5, При этом изображение
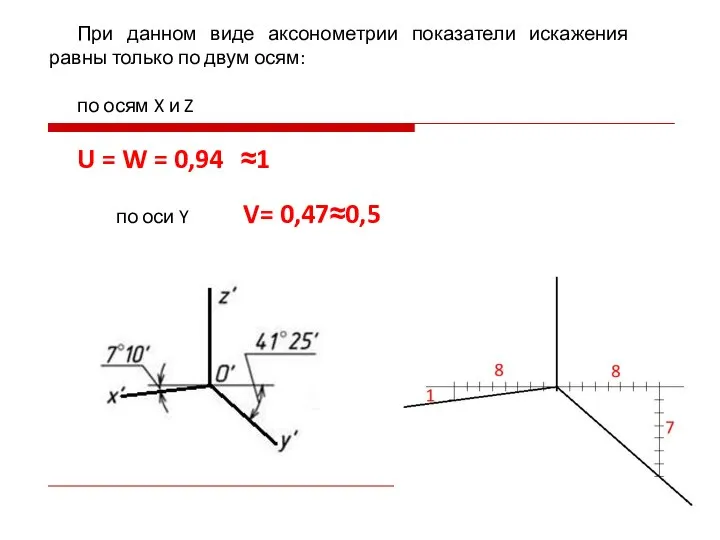
- 19. При данном виде аксонометрии показатели искажения равны только по двум осям: по осям X и Z
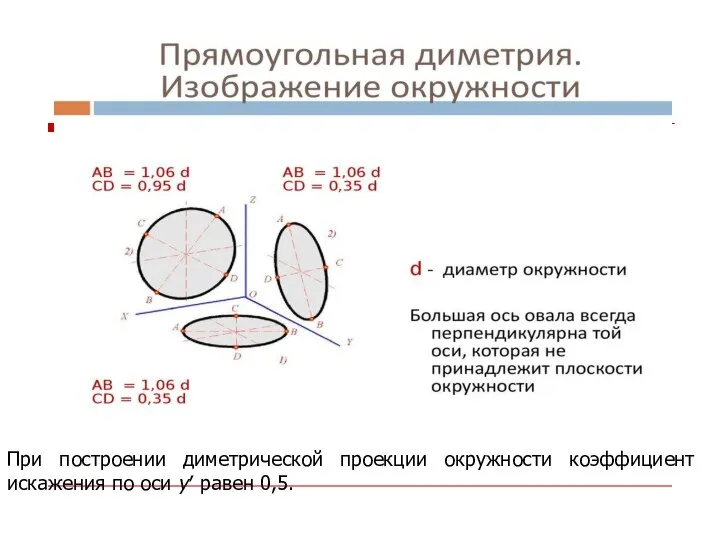
- 20. Окружности, параллельные координатным плоскостям, представляют собой эллипсы двух видов. БОЭ перпендикулярны соответствующим аксонометрическим осям, а МОЭ
- 21. При построении диметрической проекции окружности коэффициент искажения по оси y′ равен 0,5.
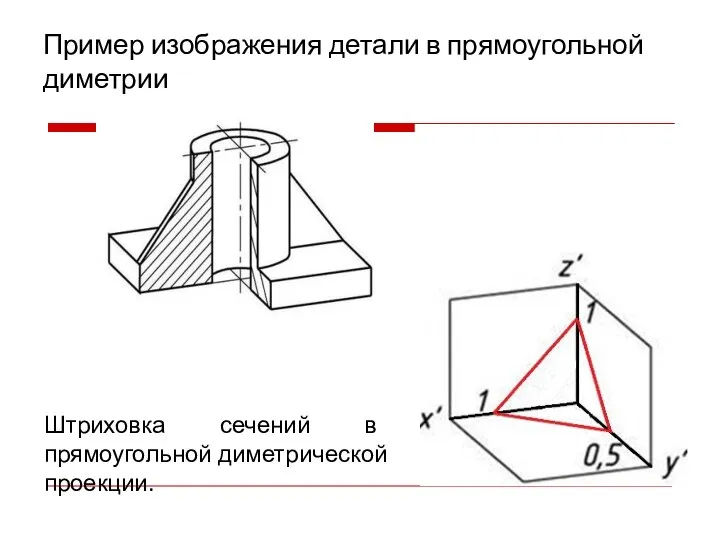
- 22. Пример изображения детали в прямоугольной диметрии Штриховка сечений в прямоугольной диметрической проекции.
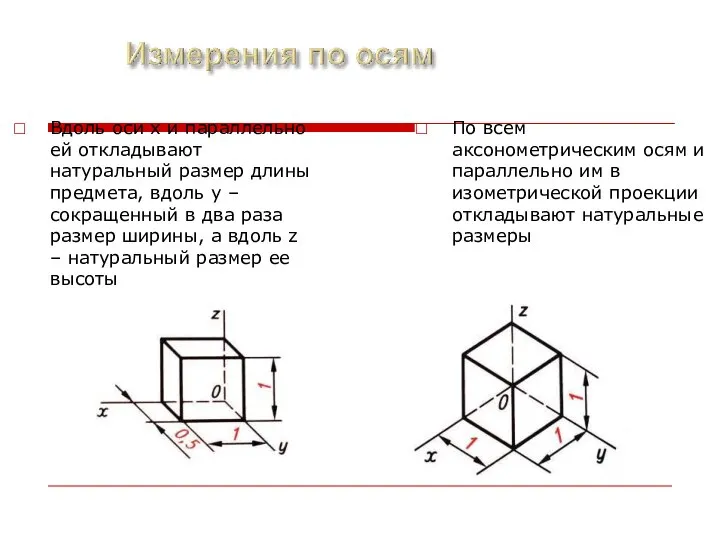
- 23. Вдоль оси x и параллельно ей откладывают натуральный размер длины предмета, вдоль y – сокращенный в
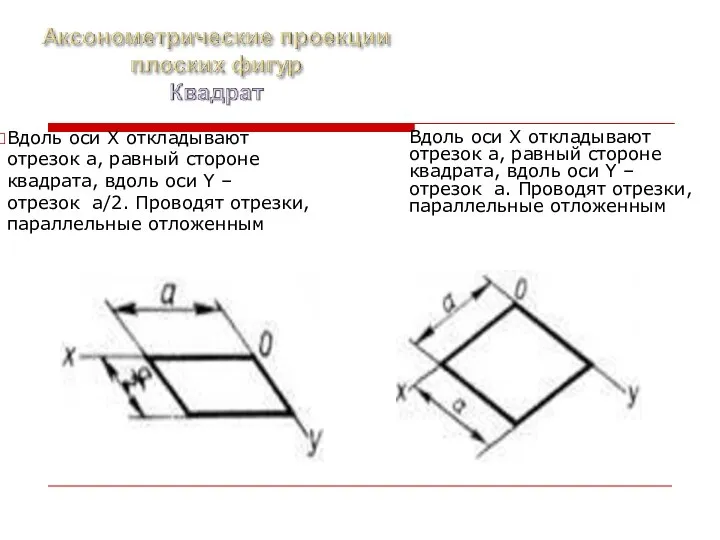
- 24. Вдоль оси X откладывают отрезок a, равный стороне квадрата, вдоль оси Y – отрезок a/2. Проводят
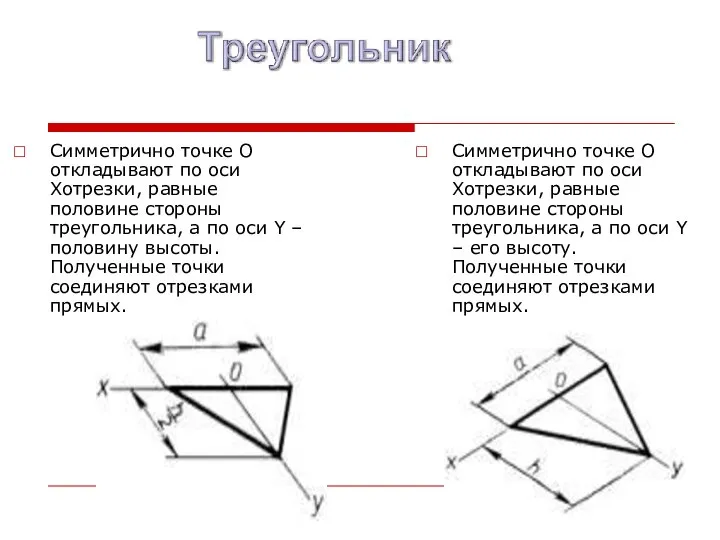
- 25. Симметрично точке O откладывают по оси Xотрезки, равные половине стороны треугольника, а по оси Y –
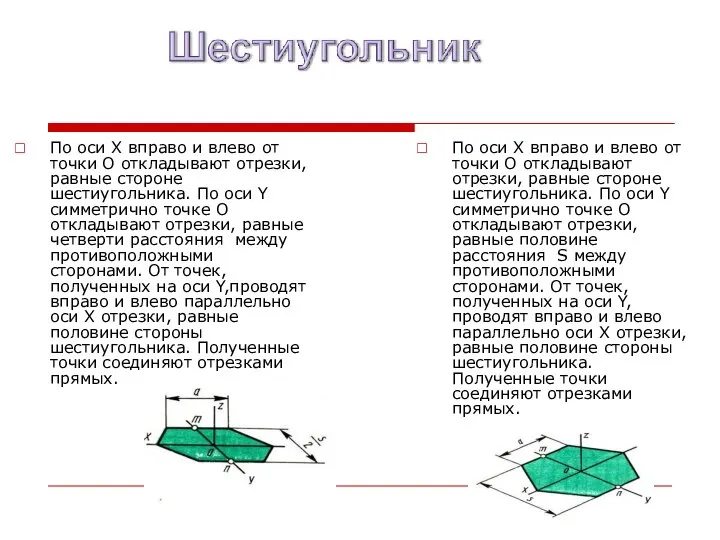
- 26. По оси X вправо и влево от точки O откладывают отрезки, равные стороне шестиугольника. По оси
- 27. Косоугольные аксонометрические проекции
- 28. Данные проекции характеризуются двумя основными признаками: плоскость аксонометрических проекций располагается параллельно одной из сторон объекта, которая
- 29. Фронтальная изометрия
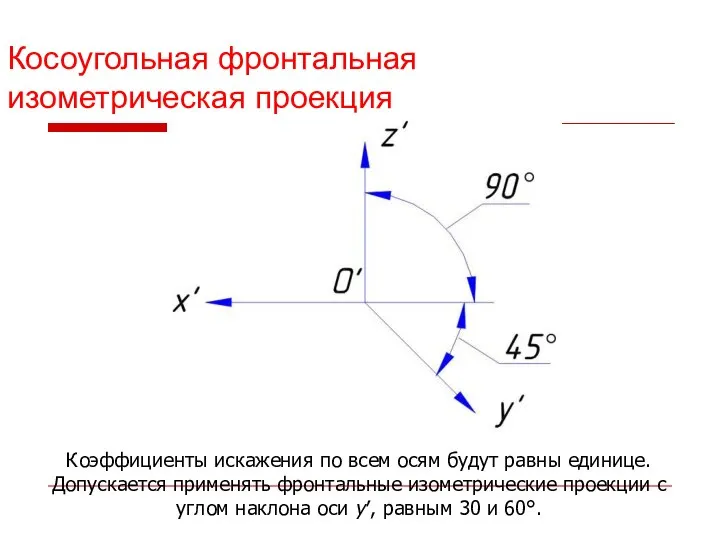
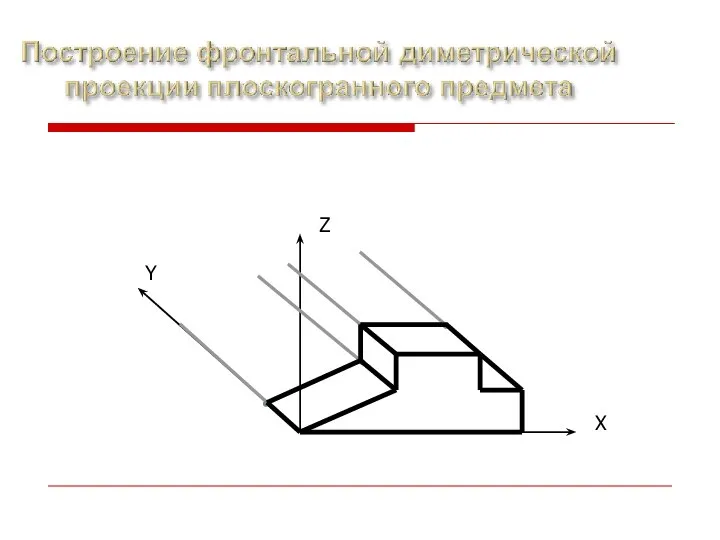
- 30. Косоугольная фронтальная изометрическая проекция Коэффициенты искажения по всем осям будут равны единице. Допускается применять фронтальные изометрические
- 31. 1 – окружность 2, 3 – эллипсы БОЭ расположена под углом 22°30′ к осям X и
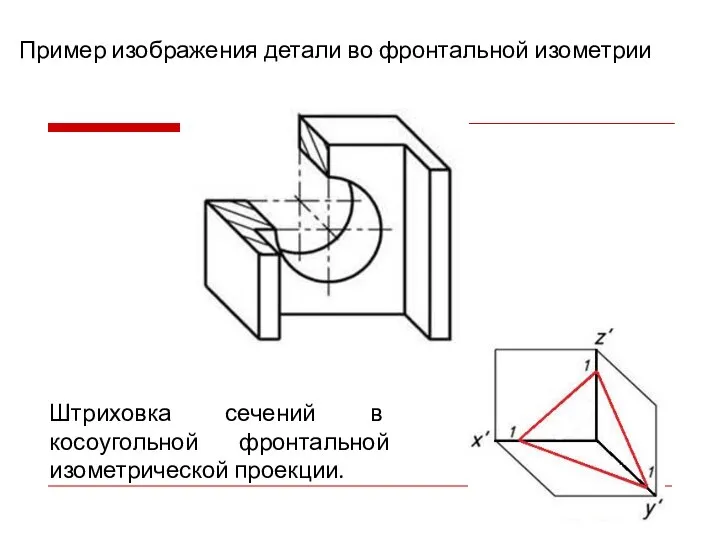
- 32. Штриховка сечений в косоугольной фронтальной изометрической проекции. Пример изображения детали во фронтальной изометрии
- 33. Фронтальная диметрия
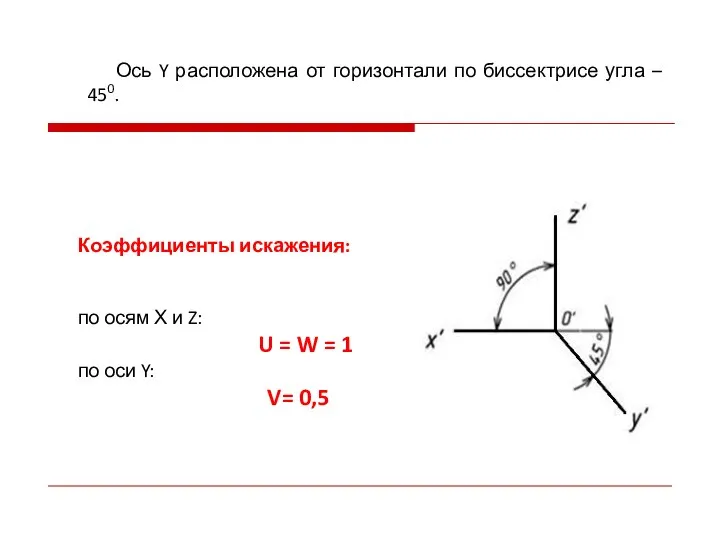
- 34. Коэффициенты искажения: по осям Х и Z: U = W = 1 по оси Y: V=
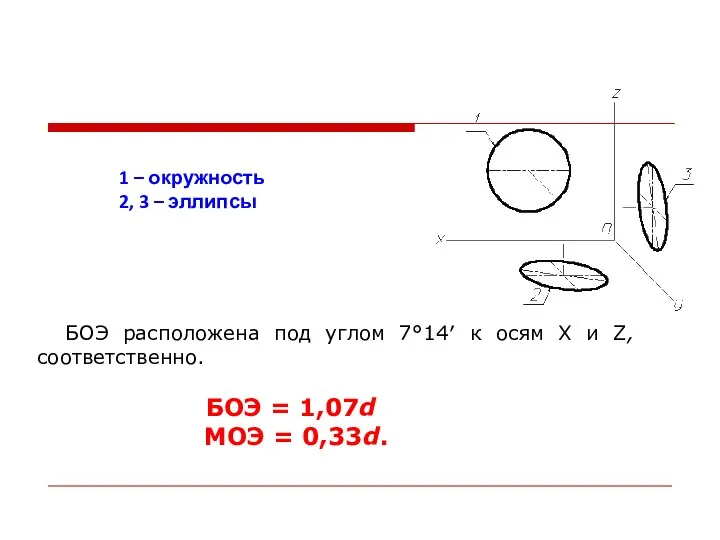
- 35. БОЭ расположена под углом 7°14′ к осям X и Z, соответственно. БОЭ = 1,07d МОЭ =
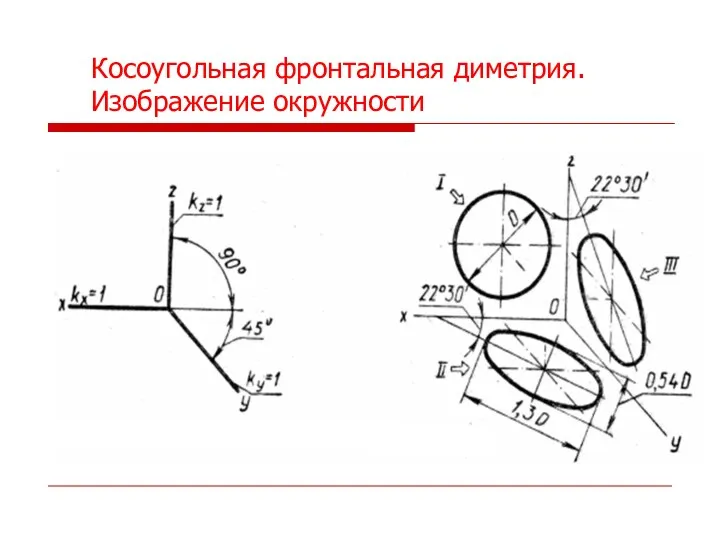
- 36. Косоугольная фронтальная диметрия. Изображение окружности
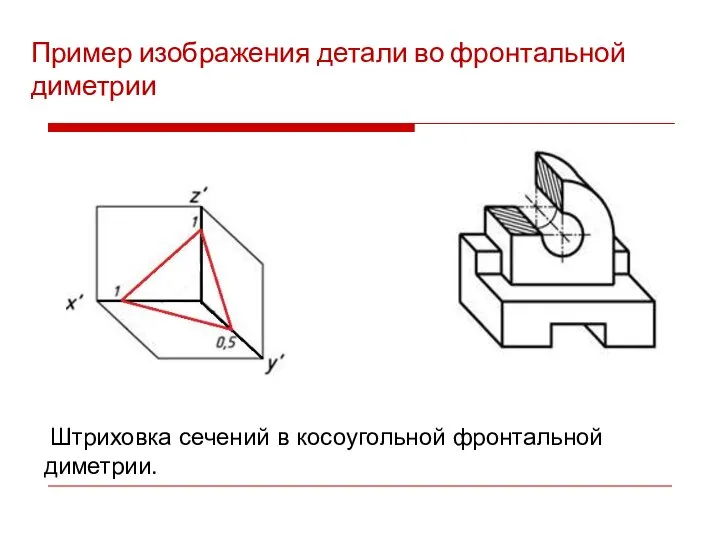
- 37. Пример изображения детали во фронтальной диметрии Штриховка сечений в косоугольной фронтальной диметрии.
- 38. Z X Y
- 39. Горизонтальная изометрия (кавальерная проекция)
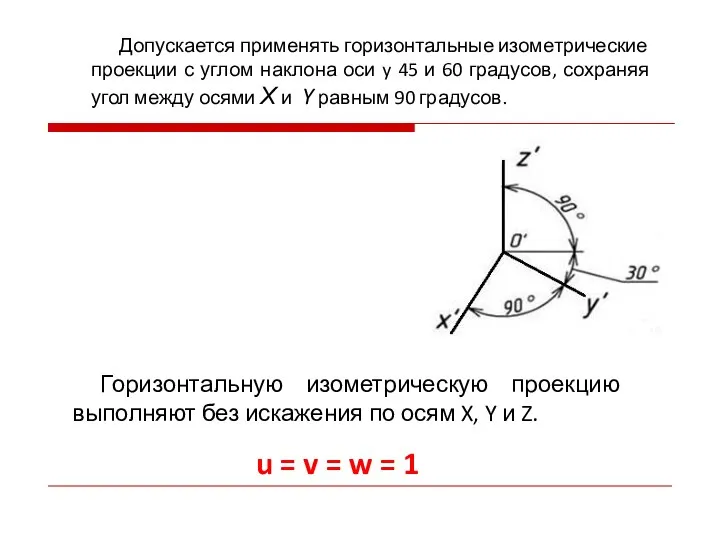
- 40. Допускается применять горизонтальные изометрические проекции с углом наклона оси y 45 и 60 градусов, сохраняя угол
- 41. Окружности, лежащие в плоскостях, параллельных горизонтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а
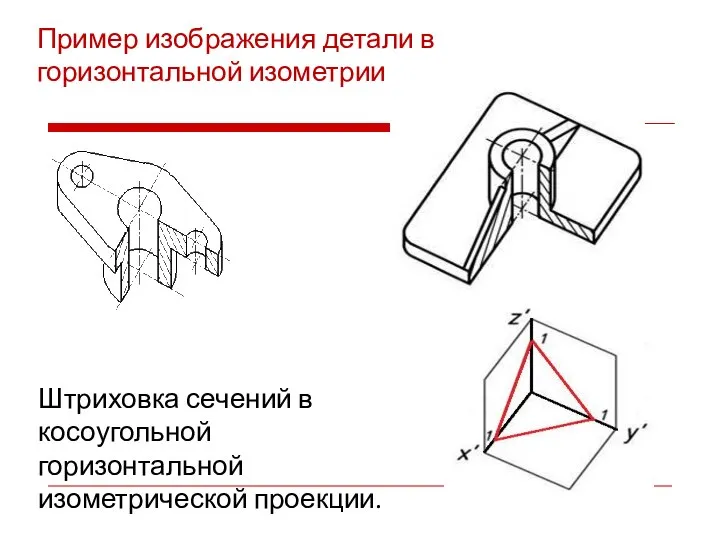
- 42. Штриховка сечений в косоугольной горизонтальной изометрической проекции. Пример изображения детали в горизонтальной изометрии
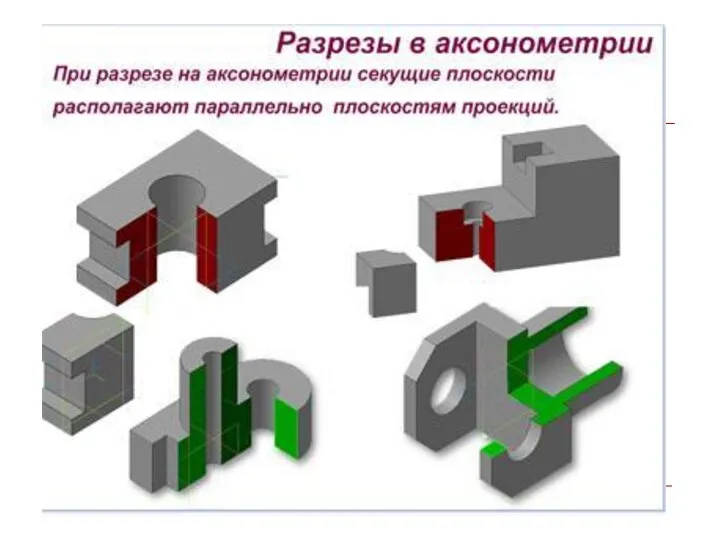
- 43. Разрезы в аксонометрических проекциях Для построения разреза (выреза) в аксонометрических проекциях используют несколько секущих плоскостей, параллельных
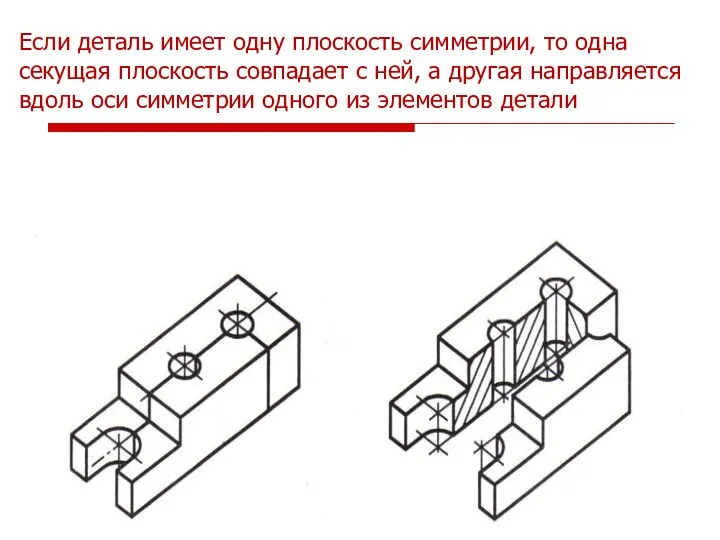
- 44. Если деталь имеет одну плоскость симметрии, то одна секущая плоскость совпадает с ней, а другая направляется
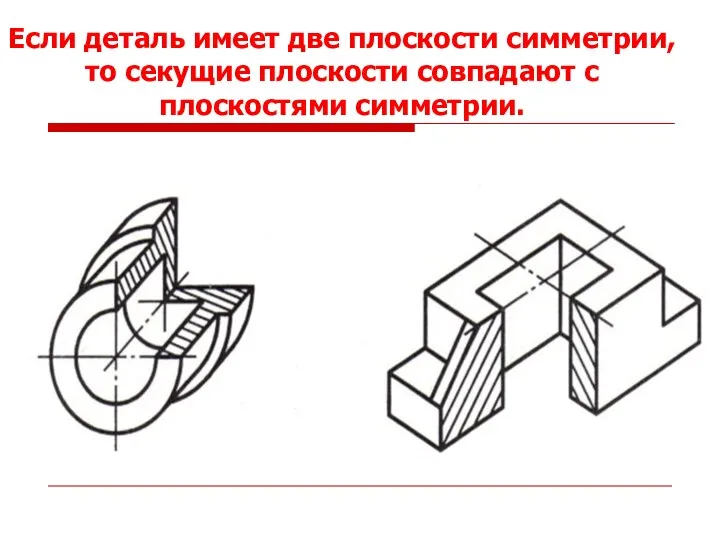
- 45. Если деталь имеет две плоскости симметрии, то секущие плоскости совпадают с плоскостями симметрии.
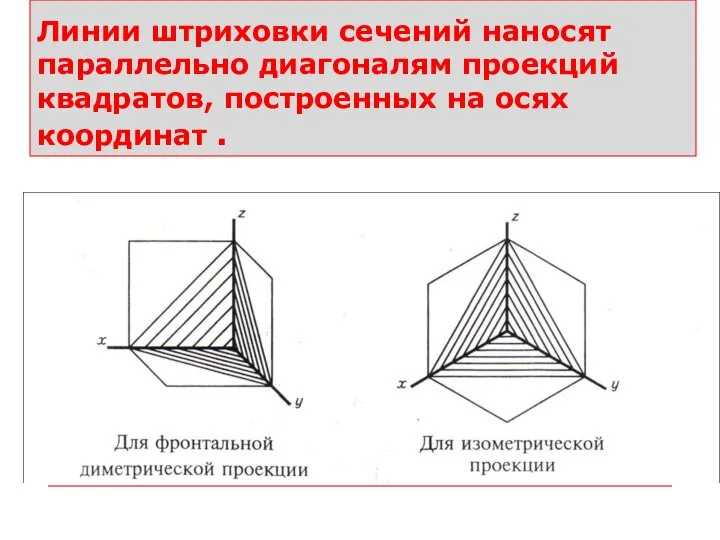
- 46. Линии штриховки сечений наносят параллельно диагоналям проекций квадратов, построенных на осях координат .
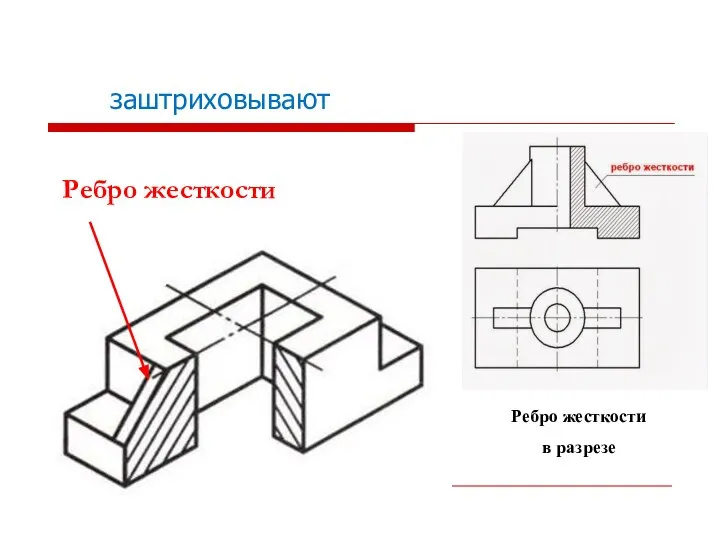
- 47. Ребро жесткости В аксонометрических проекциях спицы колес, ребра жесткости и подобные элементы, попавшие в разрез, заштриховывают
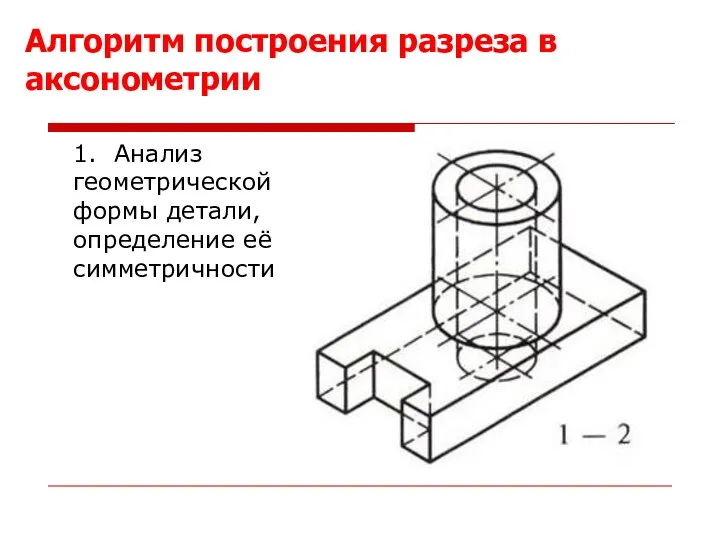
- 49. 1. Анализ геометрической формы детали, определение её симметричности Алгоритм построения разреза в аксонометрии
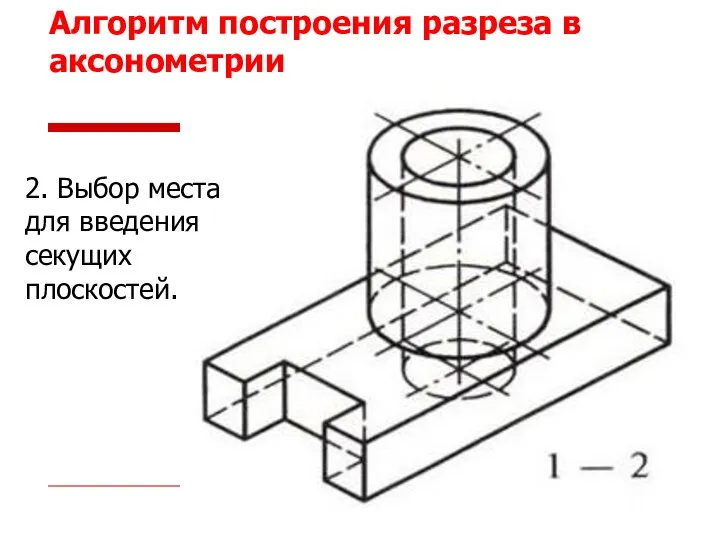
- 50. Алгоритм построения разреза в аксонометрии 2. Выбор места для введения секущих плоскостей.
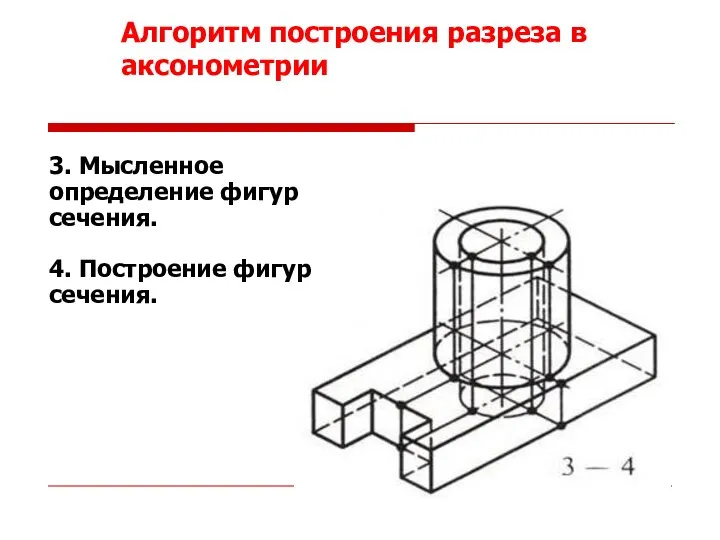
- 51. 3. Мысленное определение фигур сечения. 4. Построение фигур сечения. Алгоритм построения разреза в аксонометрии
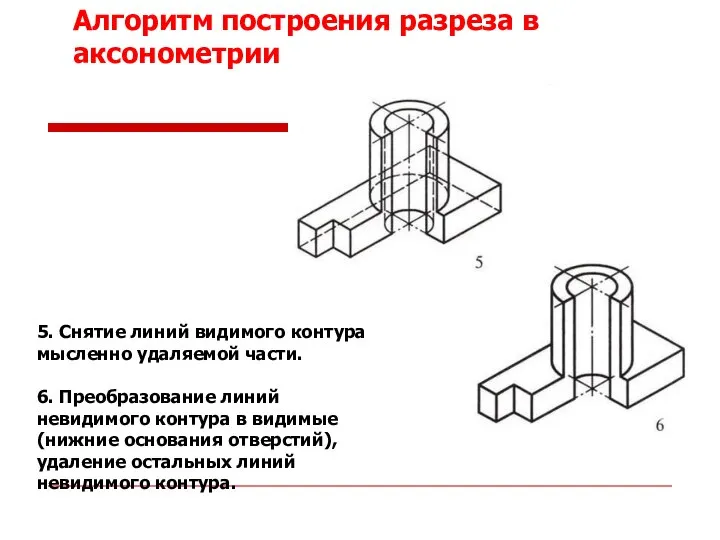
- 52. 5. Снятие линий видимого контура мысленно удаляемой части. 6. Преобразование линий невидимого контура в видимые (нижние
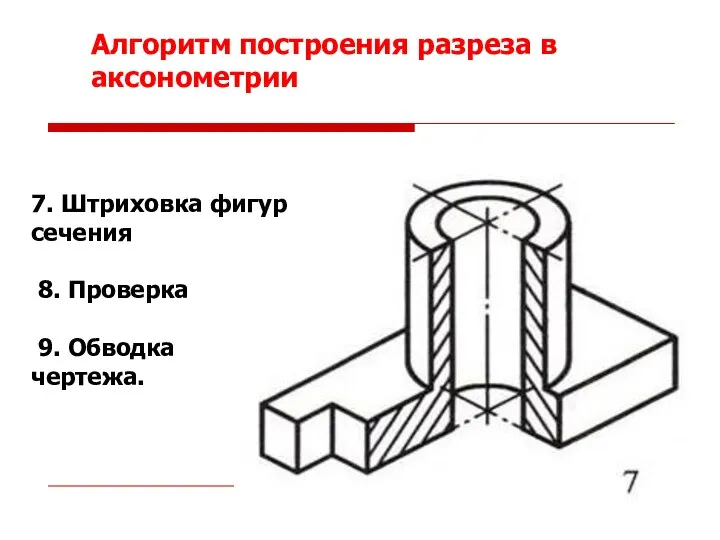
- 53. 7. Штриховка фигур сечения 8. Проверка 9. Обводка чертежа. Алгоритм построения разреза в аксонометрии
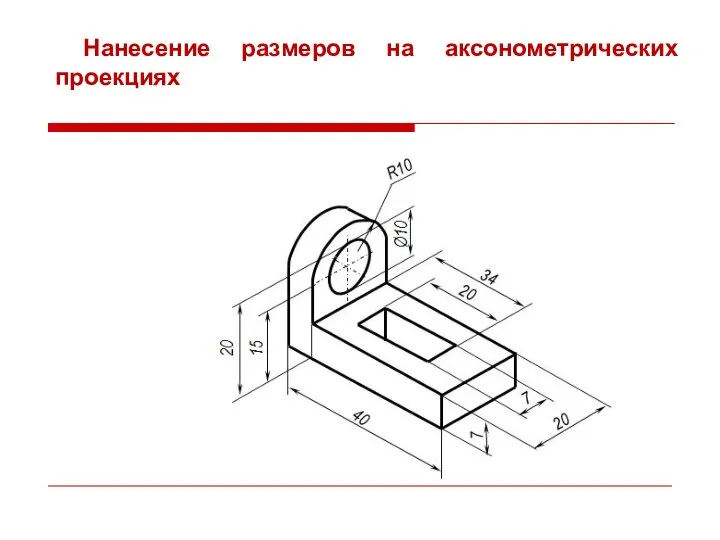
- 54. Нанесение размеров на аксонометрических проекциях
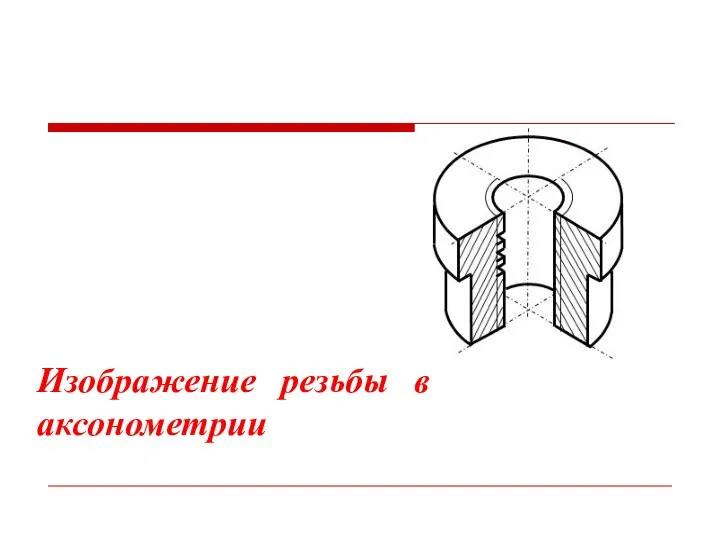
- 55. Изображение резьбы в аксонометрии
- 56. Выбор аксонометрических проекций
- 57. Выбор аксонометрических проекций при построении изображений может подчиняться различным требованиям. Главные из них – наглядность и
- 59. Скачать презентацию

















 Дифференциальная диагностика нейроинфекций
Дифференциальная диагностика нейроинфекций Формы записи алгоритмов
Формы записи алгоритмов В зоопарке
В зоопарке Суффиксы
Суффиксы «Создание сообщества для разработки и реализации системы дистанционной диагностики»
«Создание сообщества для разработки и реализации системы дистанционной диагностики» ИТОГИ РАЗВИТИЯ ЭКОНОМИКИ И СОЦИАЛЬНОЙ СФЕРЫ КЕМЕРОВСКОЙ ОБЛАСТИ В 2008 ГОДУ
ИТОГИ РАЗВИТИЯ ЭКОНОМИКИ И СОЦИАЛЬНОЙ СФЕРЫ КЕМЕРОВСКОЙ ОБЛАСТИ В 2008 ГОДУ Описание уровней развития отношения ребенка к той или иной ценности.Это - не точный диагноз, это – тенденция, повод для Вашего пед
Описание уровней развития отношения ребенка к той или иной ценности.Это - не точный диагноз, это – тенденция, повод для Вашего пед кроссворд1
кроссворд1 Телерадиожурналистика
Телерадиожурналистика О Б Р А З И В А Н У Ш К И - Д У Р А Ч К А
О Б Р А З И В А Н У Ш К И - Д У Р А Ч К А Лубочные картинки как первые комиксы
Лубочные картинки как первые комиксы Финансовый рынок
Финансовый рынок Презентация на тему Электробезопасность Опасности электрических систем
Презентация на тему Электробезопасность Опасности электрических систем  Диалог-форум «Долгосрочное накопительное страхование в России»О проекте Стратегии развития страхового рынка до 2020 года. Пробле
Диалог-форум «Долгосрочное накопительное страхование в России»О проекте Стратегии развития страхового рынка до 2020 года. Пробле Дмитрий Иванович Менделеев (1834–1907)
Дмитрий Иванович Менделеев (1834–1907) Исследовательский проект на тему:
Исследовательский проект на тему: Художник и ученый
Художник и ученый Роль преподавателя в повышении качества обучения в условиях дистанционного образования
Роль преподавателя в повышении качества обучения в условиях дистанционного образования Нарушения родовой деятельности
Нарушения родовой деятельности Собственные имена
Собственные имена СЮРВЕЙ И СТРАХОВАНИЕ
СЮРВЕЙ И СТРАХОВАНИЕ Анализ. Контекст. Постановка исследовательского вопроса
Анализ. Контекст. Постановка исследовательского вопроса Презентация на тему Битва на Чудском озере
Презентация на тему Битва на Чудском озере  Путешествие по Солнечной системе
Путешествие по Солнечной системе Школьная жизнь в фактах и цифрах
Школьная жизнь в фактах и цифрах Сленгізм дерибанити в українському медіаполітичному дискурсі: семантико-дистрибутивний аналіз
Сленгізм дерибанити в українському медіаполітичному дискурсі: семантико-дистрибутивний аналіз Маршрутная сеть автобусов
Маршрутная сеть автобусов Презентация на тему Источники света. Распространение света
Презентация на тему Источники света. Распространение света