Содержание
- 2. Девиз урока: Скажи мне, и я забуду Покажи мне ,и я запомню Дай действовать самому И
- 3. Цели урока: Обучающие: систематизировать знания и умения по теме «Производная»: формулы и правила дифференцирования, геометрический и
- 4. Повторение
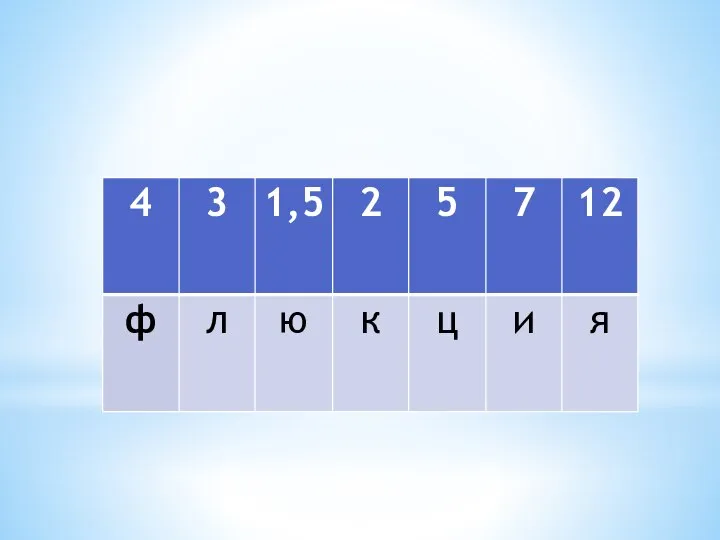
- 5. Задание : Расшифруйте слово
- 8. Понятие "производная" возникло в связи с необходимостью решения ряда задач физики, механики и математики. Честь открытия
- 9. Тестовая работа
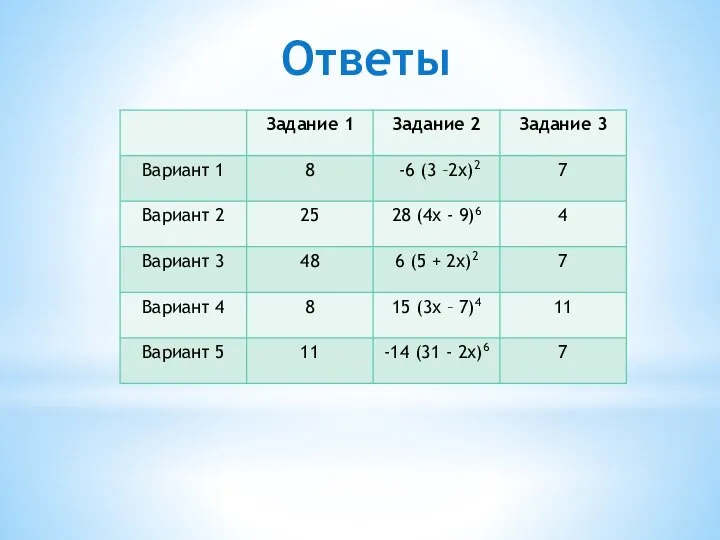
- 10. Ответы
- 11. Потренируемся:
- 12. Задания ЕГЭ 2011 В-8
- 13. 1 0 1 4 2 Задание №1. На рисунке изображён график функции y = f(x) и
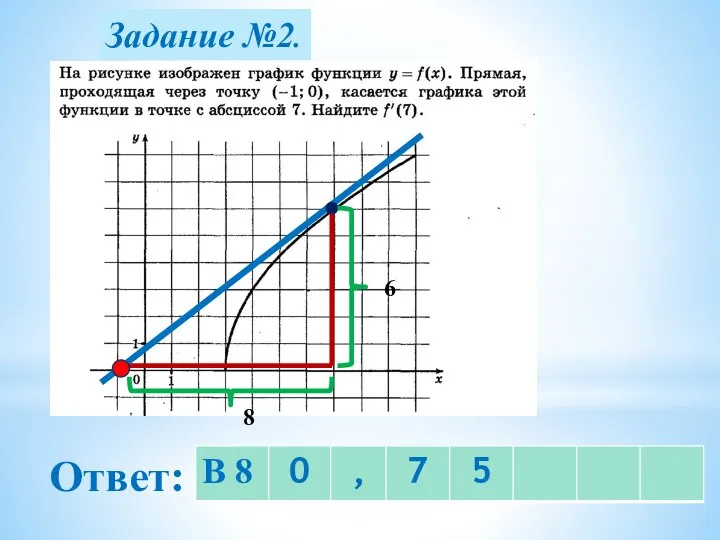
- 14. Задание №2. Ответ: 6 8
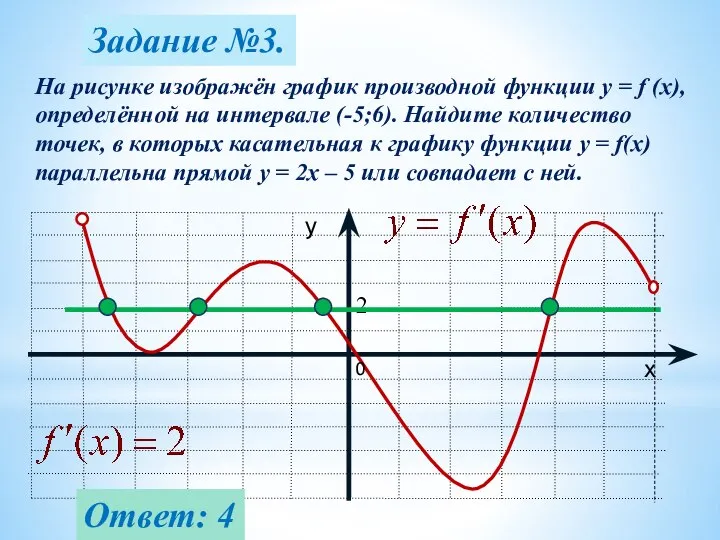
- 15. Задание №3. На рисунке изображён график производной функции y = f (x), определённой на интервале (-5;6).
- 16. Задание №4 Задание №5 Ответ: Ответ:
- 17. Задача № 1 Материальная точка движется прямолинейно по закону x (t) = 6 t² - 48
- 18. Решение Найдем производную функции x (t) = 6 t² - 48 t +17 x’ (t) =
- 19. Задача № 2 Решение. Если нам известна скорость точки в некий момент времени, следовательно нам известно
- 20. Решите самостоятельно следующие задания
- 21. Самостоятельная работа Вариант 1 Вариант 2
- 22. Ответы
- 23. Ну кто придумал эту математику ! У меня всё получилось!!! Надо решить ещё пару примеров. Рефлексия
- 25. Скачать презентацию

















 Средняя линия треугольника
Средняя линия треугольника Задачи на нахождение площади треугольника
Задачи на нахождение площади треугольника Решение задач по теме: Терема Пифагора
Решение задач по теме: Терема Пифагора Параллельность плоскостей
Параллельность плоскостей Сумма углов в треугольнике
Сумма углов в треугольнике Раздел 3. Линейная алгебра с элементами аналитической геометрии
Раздел 3. Линейная алгебра с элементами аналитической геометрии Дидактическая игра. Какого фрагмента не хватает на картинке (для дошкольников)
Дидактическая игра. Какого фрагмента не хватает на картинке (для дошкольников) Правильная пирамида
Правильная пирамида Вычитаем числа
Вычитаем числа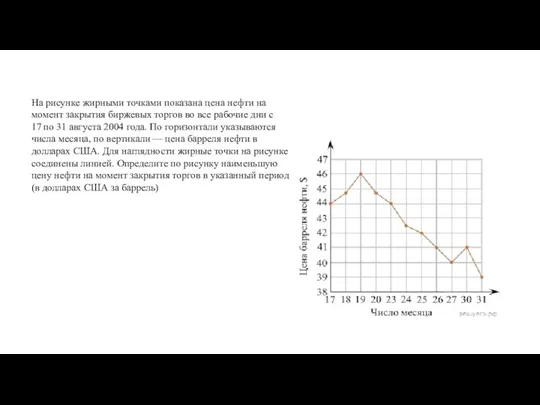 Вариант 1
Вариант 1 Двугранные углы
Двугранные углы Треугольники
Треугольники Решение задач с помощью уравнений
Решение задач с помощью уравнений Пересекающиеся и параллельные прямые
Пересекающиеся и параллельные прямые Презентация на тему Сложение и вычитание дробей с разными знаменателями
Презентация на тему Сложение и вычитание дробей с разными знаменателями  Прямая, кривая, ломаная
Прямая, кривая, ломаная Основы векторного исчисления
Основы векторного исчисления Проценты чисел
Проценты чисел Векторы
Векторы Используется ли в учебниках 7-го класса термин Функциональная зависимость?
Используется ли в учебниках 7-го класса термин Функциональная зависимость? Решение задач. 1 класс
Решение задач. 1 класс Прямая. Тест
Прямая. Тест Уравнение с двумя переменными
Уравнение с двумя переменными Математическое моделирование. Воспроизводимость опытов
Математическое моделирование. Воспроизводимость опытов Вікористання спадщини видатних математиків Полтавщини на уроках математики
Вікористання спадщини видатних математиків Полтавщини на уроках математики Теорема Пифагора
Теорема Пифагора Презентация на тему ГИА 2013. Модуль Геометрия №10
Презентация на тему ГИА 2013. Модуль Геометрия №10  Объем. Цилиндр, призма
Объем. Цилиндр, призма