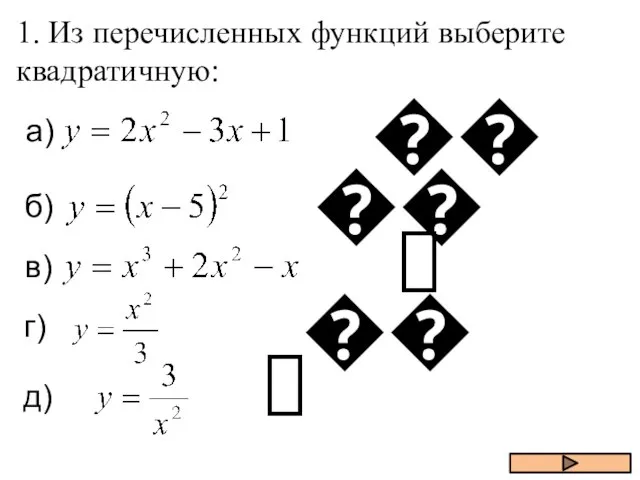
Слайд 21. Из перечисленных функций выберите квадратичную:
?
?
?
?
?
Слайд 3а)
2. Укажите направление ветвей параболы

Слайд 4а)
3. Составьте уравнение оси симметрии параболы

Слайд 5Алгоритм построения параболы
Найти координаты вершины параболы
На координатной плоскости провести ось симметрии параболы

и отметить вершину параболы.
Заполнить таблицу.
Отметить точки на координатной плоскости и провести параболу.
Слайд 6Построить график функции
Найти координаты вершины параболы

Слайд 8Найти наименьшее и наибольшее значения функции на отрезке [0; 3].
x
y
1
1
-2
-5
2
3
-3
O
![Найти наименьшее и наибольшее значения функции на отрезке [0; 3]. x y](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/460385/slide-7.jpg)
Слайд 9№22.19. Построить график функции
Найдём координаты вершины параболы
- ось симметрии параболы
- вершина параболы
квадратичная

функция, графиком является парабола, ветви направлены вниз.
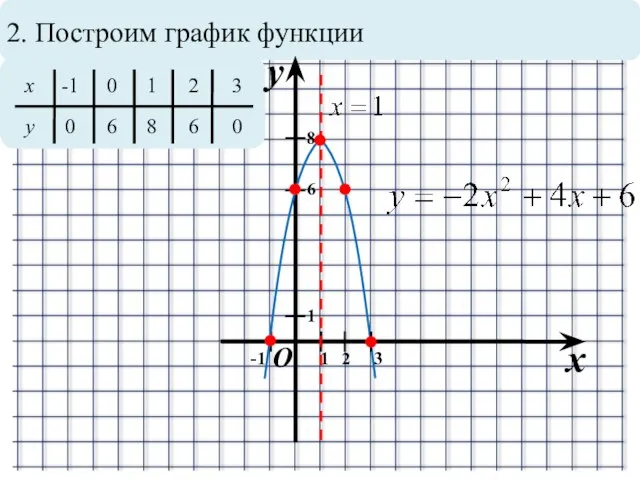
Слайд 102. Построим график функции
x
y
O
1
1
-1
2
8
x
-1
0
1
2
3
y
0
6
8
6
0
6
3
Слайд 113. Чтение графика
x
y
O
1
1
-1
2
8
6
3
а) y(-2)=
-10
y(0)=
6
y(3)=
0
-2
б) y=-10 при x=
-2 или x=4
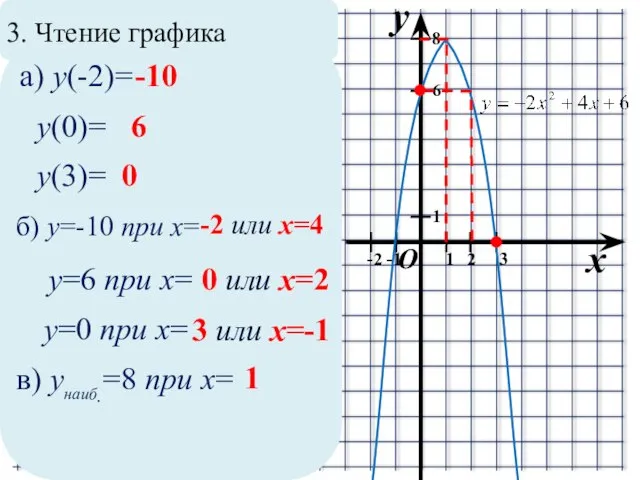
y=6 при x=
0 или x=2
y=0 при x=
3 или x=-1
в) yнаиб.=8 при x=
1
Слайд 123. Чтение графика
x
y
O
1
1
-1
2
8
6
3
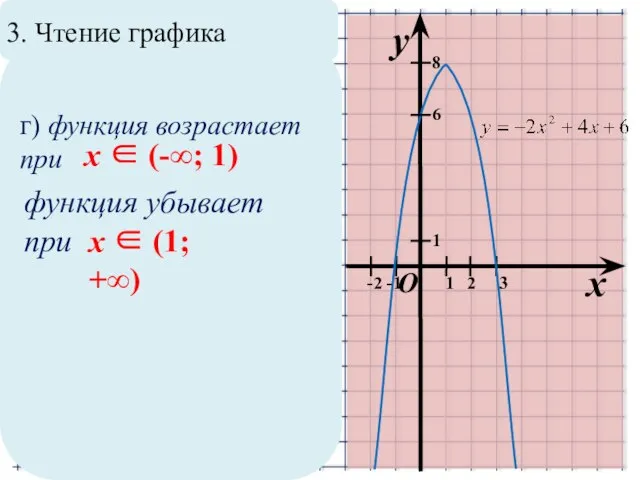
г) функция возрастает при
x ∈ (-∞; 1)
функция убывает при
x
Слайд 133. Чтение графика
x
y
O
1
1
2
8
6
3
д) y > 0 при
x ∈ (-1; 3)
y <
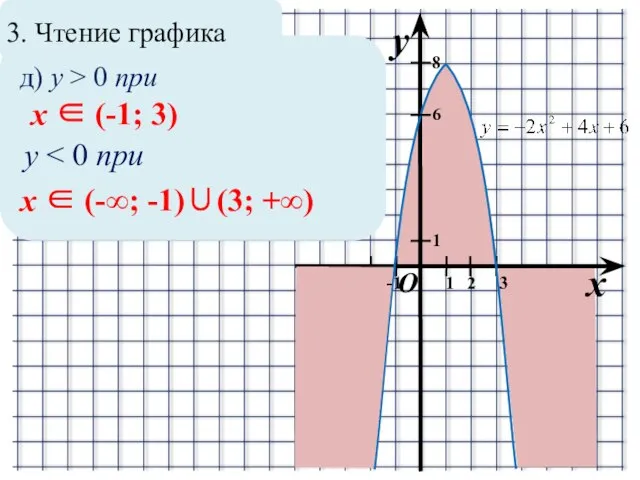
0 при
x ∈ (-∞; -1)∪(3; +∞)
-2
-1
Слайд 14№22.16. Найдите наибольшее и наименьшее значения функции
Найдём координаты вершины параболы
- ось симметрии

параболы
- вершина параболы
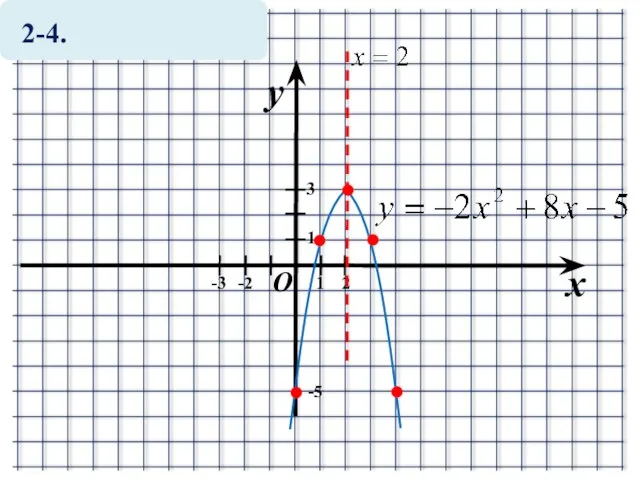
Слайд 15а) на отрезке [0; 2]
x
y
1
1
-2
-5
2
4
O
yнаиб.=4 при x=1
yнаим.=3 при x=0 или x=2
3
б) на
![а) на отрезке [0; 2] x y 1 1 -2 -5 2](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/460385/slide-14.jpg)
луче (-∞; 1]
yнаиб.=4 при x=1
yнаим. не существует
в) на отрезке [1; 2]
yнаиб.=4 при x=1
yнаим.=3 при x=2
б) на луче [2; +∞)
yнаиб.=3 при x=2
yнаим. не существует





![Найти наименьшее и наибольшее значения функции на отрезке [0; 3]. x y](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/460385/slide-7.jpg)






![а) на отрезке [0; 2] x y 1 1 -2 -5 2](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/460385/slide-14.jpg)
 Общая характеристика ресурсной базы социально-культурной деятельности
Общая характеристика ресурсной базы социально-культурной деятельности Новая Редполитика
Новая Редполитика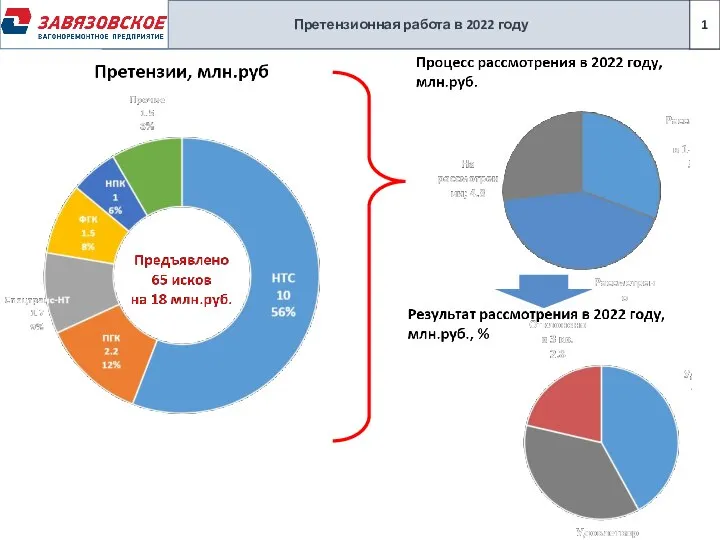 Претензии
Претензии История немецкой валюты
История немецкой валюты Современные средства оснащения образовательных учреждений
Современные средства оснащения образовательных учреждений Картинная галерея. Пейзажи
Картинная галерея. Пейзажи Александр III и его внутренняя политика
Александр III и его внутренняя политика Нумерация. Счёт предметов. Разряды
Нумерация. Счёт предметов. Разряды Дед Мороз и Снегурочка
Дед Мороз и Снегурочка Пушкинские места
Пушкинские места Традиции духовно-нравственного воспитания у народов России
Традиции духовно-нравственного воспитания у народов России Презентация на тему Разряды наречий по значению
Презентация на тему Разряды наречий по значению Времена года в творчестве А.С.Пушкина
Времена года в творчестве А.С.Пушкина Авторское право
Авторское право Ученик года-2021 6 а класс
Ученик года-2021 6 а класс От пандоры до модели…
От пандоры до модели… Применение лазерных технологий в обработке материалов в ювелирной отрасли
Применение лазерных технологий в обработке материалов в ювелирной отрасли Российские программы с мировым именем!
Российские программы с мировым именем! Как не разбиться в тумане
Как не разбиться в тумане Игровая технология
Игровая технология Firmensortiment
Firmensortiment Оценка и моделирование пенсионных обязательств
Оценка и моделирование пенсионных обязательств Занятость и социальная защита населения
Занятость и социальная защита населения Помещение на ул. Греческая, д. 69, г. Таганрог
Помещение на ул. Греческая, д. 69, г. Таганрог Совместная проектная деятельность обучающихся как инструмент творческой интеграции
Совместная проектная деятельность обучающихся как инструмент творческой интеграции Гумилёв Николай Степанович
Гумилёв Николай Степанович Презентация на тему Что такое ноосфера
Презентация на тему Что такое ноосфера  Высокое возрождение. Леонардо да Винчи. Рафаэль Санти
Высокое возрождение. Леонардо да Винчи. Рафаэль Санти