Содержание
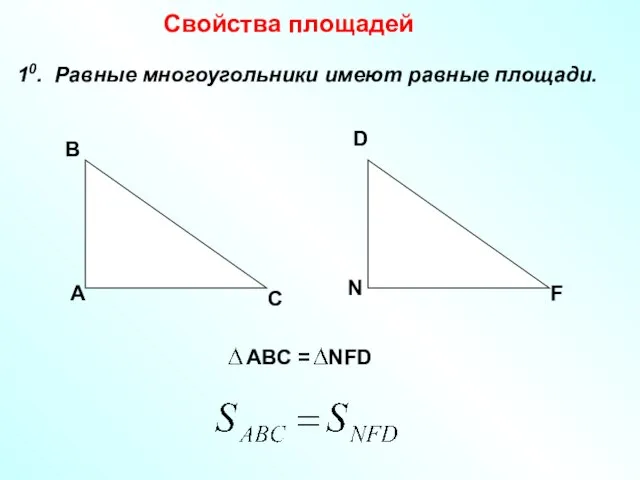
- 2. Свойства площадей 10. Равные многоугольники имеют равные площади. А В С
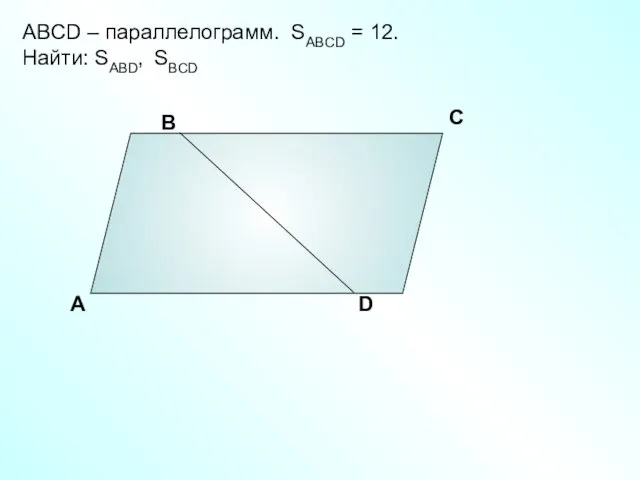
- 3. А В С D ABCD – параллелограмм. SABCD = 12. Найти: SABD, SBCD
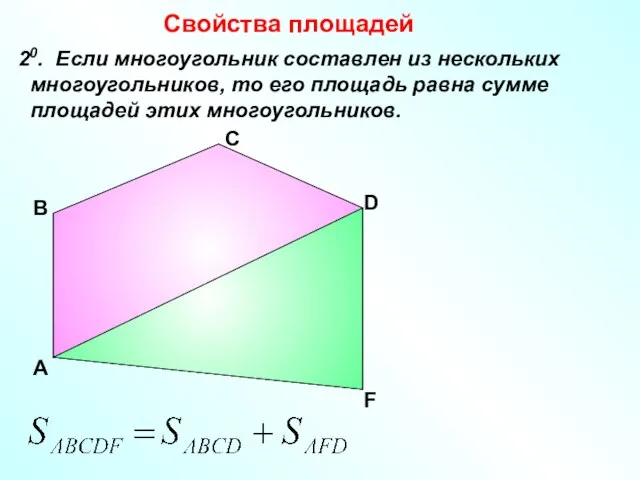
- 4. Свойства площадей 20. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих
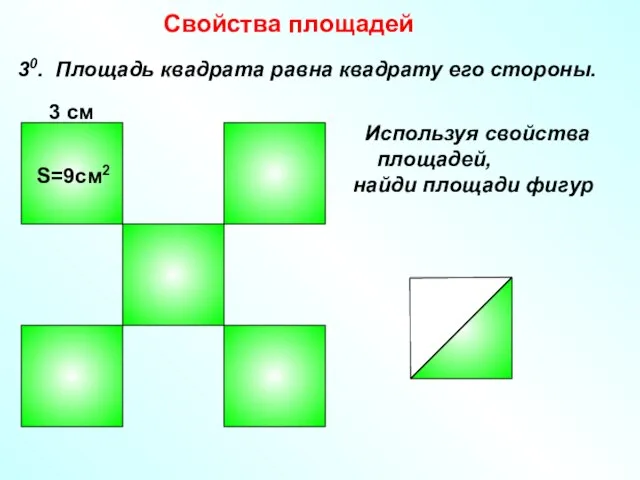
- 5. Свойства площадей 30. Площадь квадрата равна квадрату его стороны. 3 см S=9см2
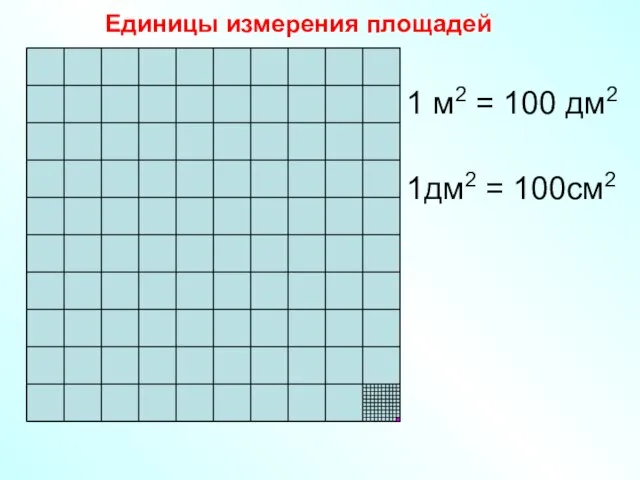
- 6. 1 м2 = 100 дм2 1дм2 = 100см2 Единицы измерения площадей
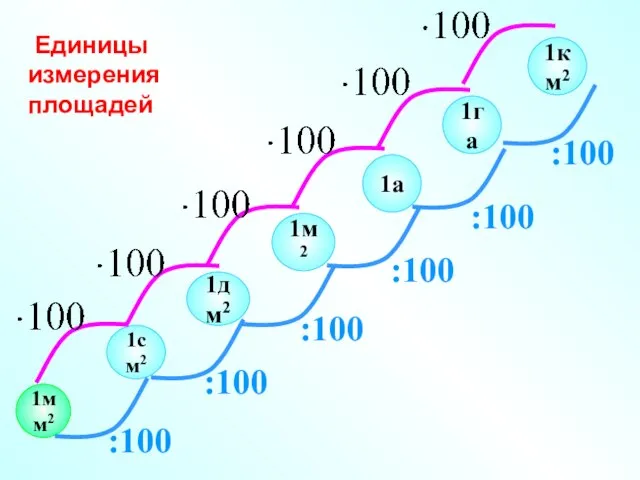
- 7. 1см2 1дм2 1м2 1га 1мм2 1км2 1а Единицы измерения площадей
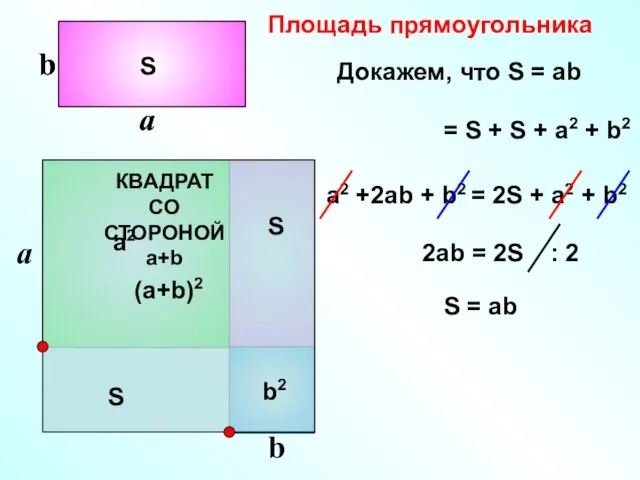
- 8. Площадь прямоугольника S (a+b)2 = S + S + a2 + b2 a2 +2ab + b2
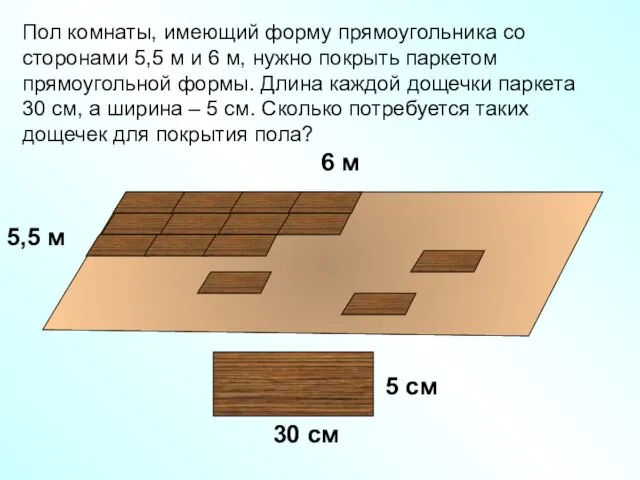
- 9. Пол комнаты, имеющий форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной
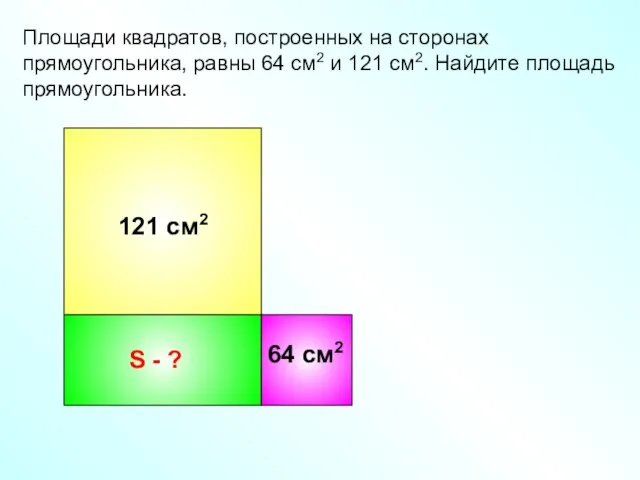
- 10. S - ? Площади квадратов, построенных на сторонах прямоугольника, равны 64 см2 и 121 см2. Найдите
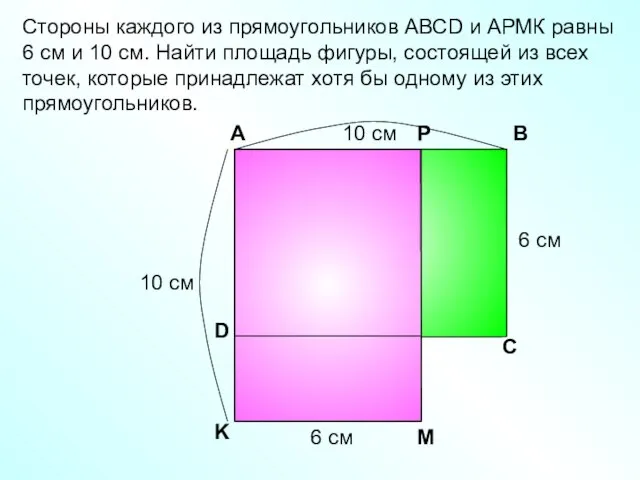
- 11. Стороны каждого из прямоугольников АВСD и АРМК равны 6 см и 10 см. Найти площадь фигуры,
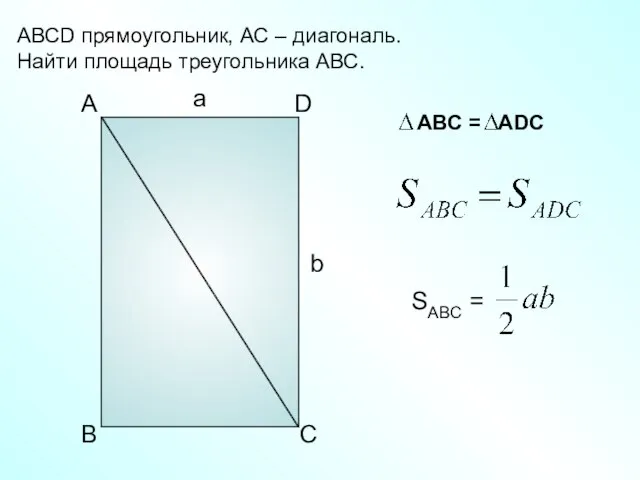
- 12. а b A D B C АВСD прямоугольник, АС – диагональ. Найти площадь треугольника АВС.
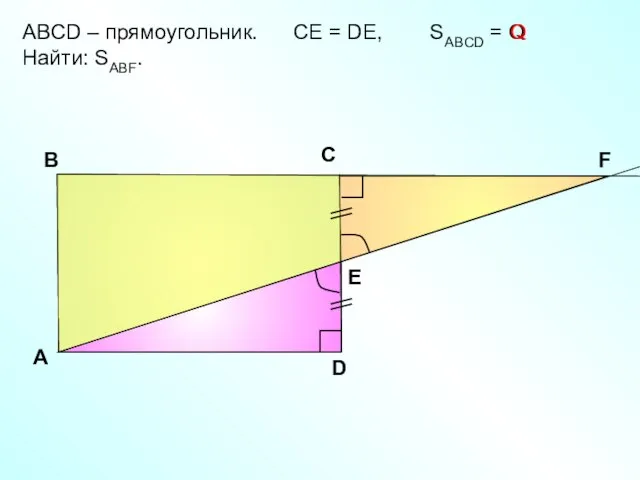
- 13. ABCD – прямоугольник. СЕ = DE, SABCD = Q Найти: SABF. A В С D Е
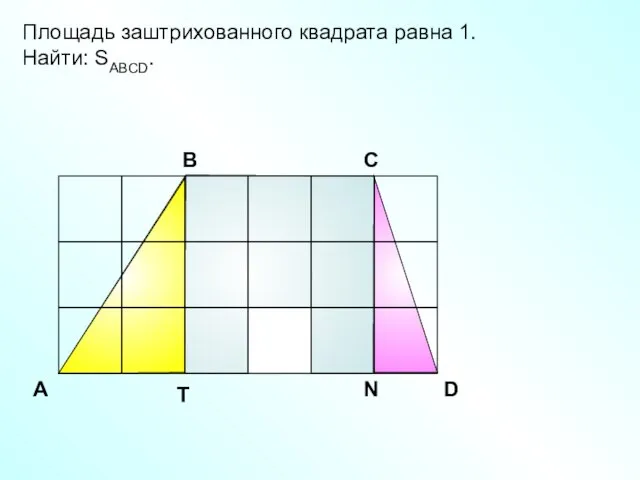
- 14. Площадь заштрихованного квадрата равна 1. Найти: SABCD. A В С D
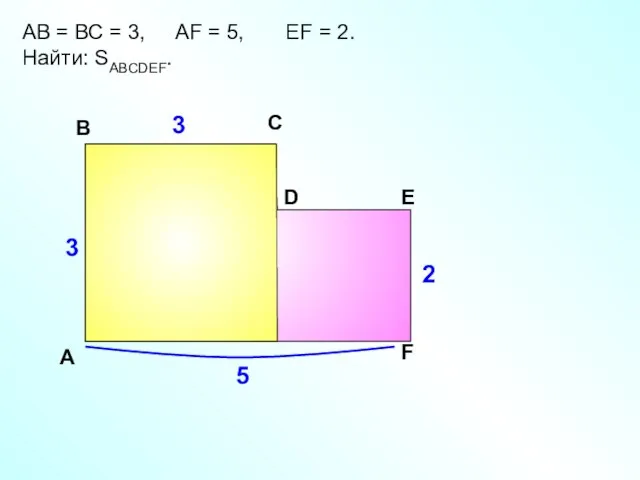
- 15. АВ = ВС = 3, АF = 5, EF = 2. Найти: SABCDEF. A В С
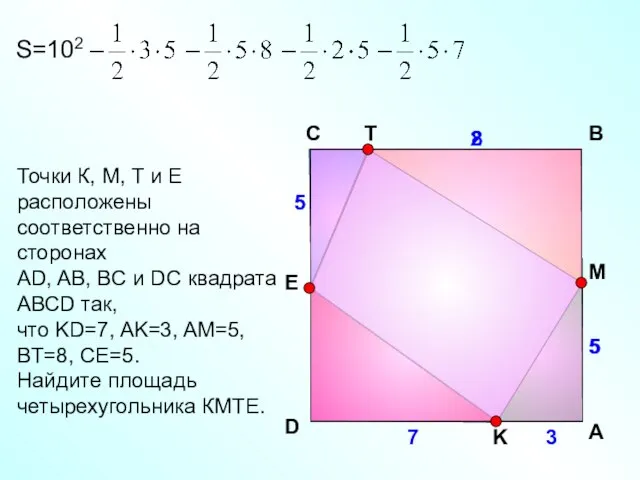
- 16. Точки К, М, Т и Е расположены соответственно на сторонах АD, AB, BC и DC квадрата
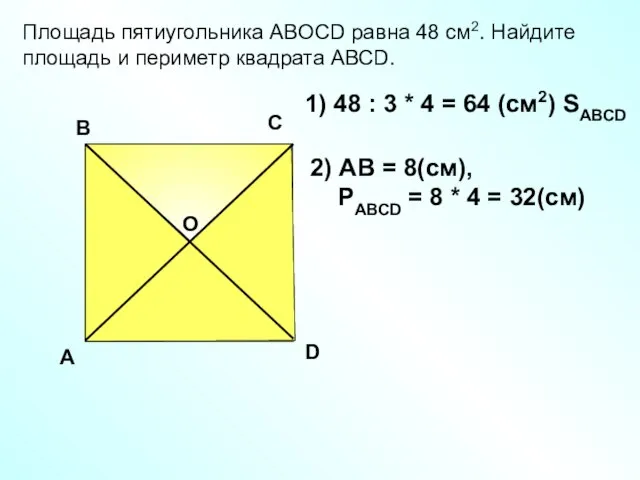
- 17. Площадь пятиугольника АBOCD равна 48 см2. Найдите площадь и периметр квадрата АВСD. A В С D
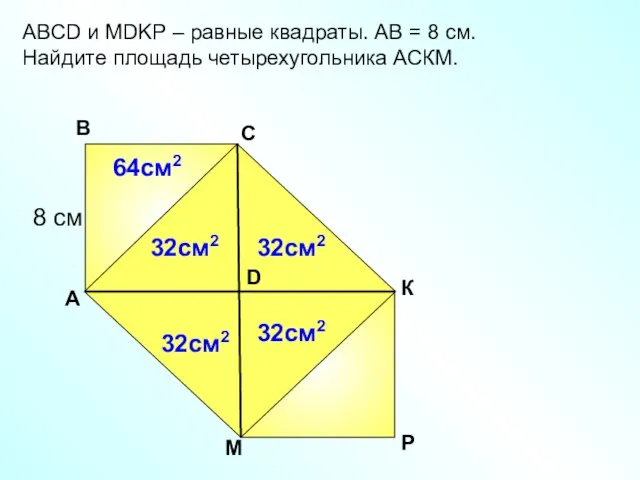
- 18. АBCD и MDKP – равные квадраты. АВ = 8 см. Найдите площадь четырехугольника АСКМ. A В
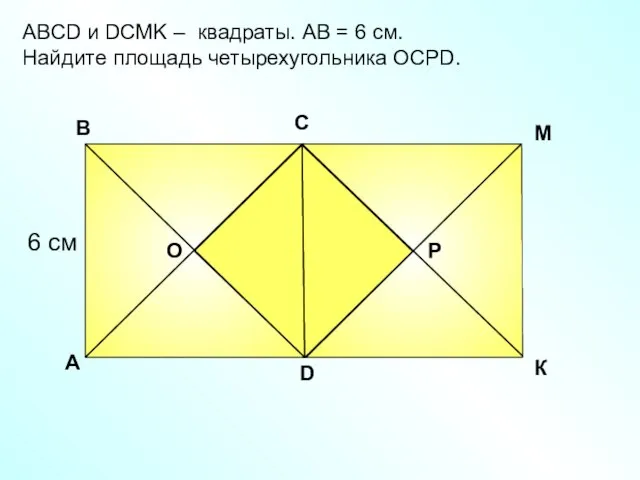
- 19. АBCD и DСМK – квадраты. АВ = 6 см. Найдите площадь четырехугольника ОСРD. A В С
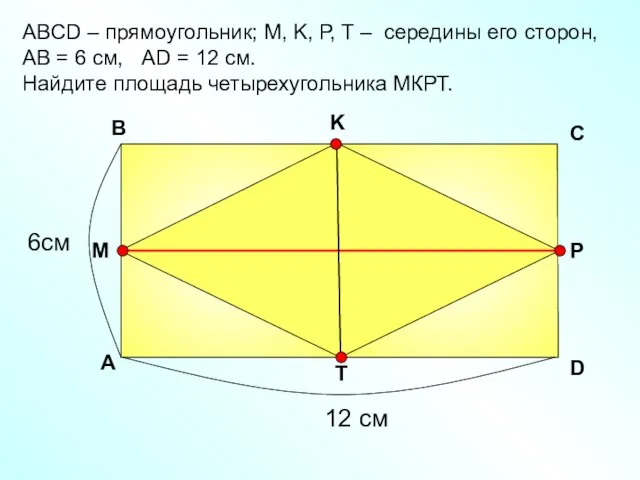
- 20. АBCD – прямоугольник; М, K, Р, Т – середины его сторон, АВ = 6 см, AD
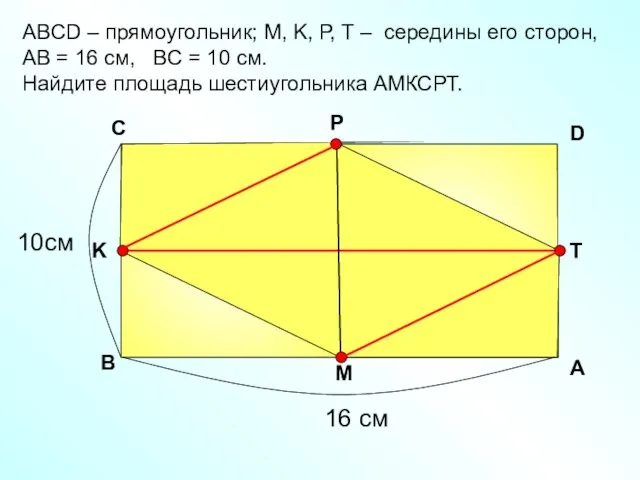
- 21. АBCD – прямоугольник; М, K, Р, Т – середины его сторон, АВ = 16 см, ВС
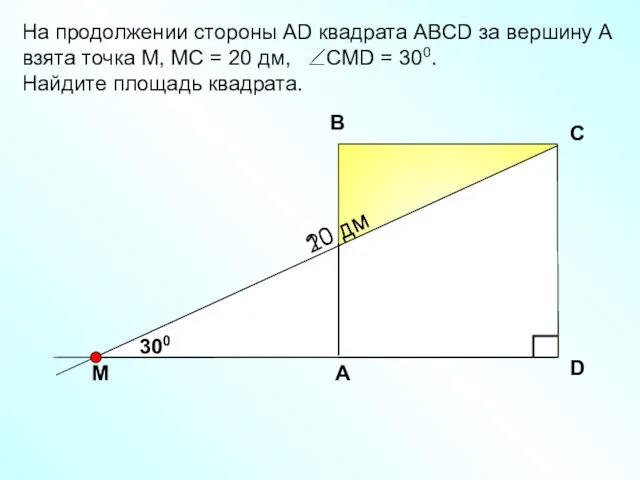
- 22. На продолжении стороны АD квадрата АBCD за вершину А взята точка М, МС = 20 дм,
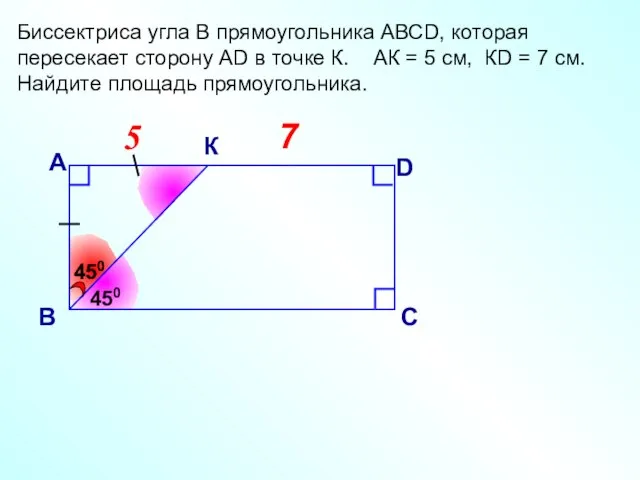
- 23. 7 5 5 Биссектриса угла В прямоугольника АВСD, которая пересекает сторону АD в точке К. АК
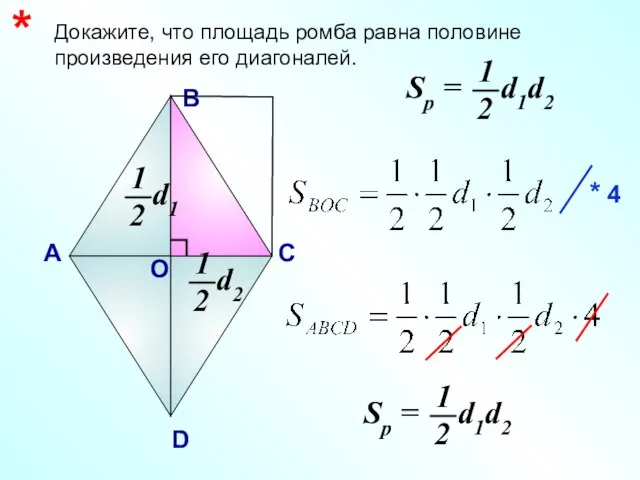
- 24. Докажите, что площадь ромба равна половине произведения его диагоналей. А В D С * О
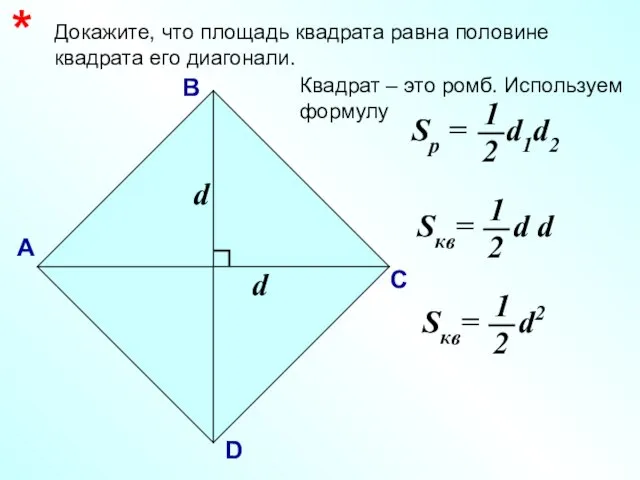
- 25. Докажите, что площадь квадрата равна половине квадрата его диагонали. * А В С D Квадрат –
- 27. Скачать презентацию
 Презентация на тему Олимпийские игры в Москве 1980
Презентация на тему Олимпийские игры в Москве 1980  Национализм как политическая идеология
Национализм как политическая идеология Презентация на тему Решение задач на нахождение площади поверхности и объемов тел вращения
Презентация на тему Решение задач на нахождение площади поверхности и объемов тел вращения  Moderní cukrovar HROCHŮV TÝNEC
Moderní cukrovar HROCHŮV TÝNEC Система работы учителя математики с родителями при подготовке учащихся к государственной итоговой аттестации в форме ЕГЭ
Система работы учителя математики с родителями при подготовке учащихся к государственной итоговой аттестации в форме ЕГЭ Внешняя политика Александра I в 1801-1812 гг.
Внешняя политика Александра I в 1801-1812 гг. Основные ошибки при подаче документов на лицензирование
Основные ошибки при подаче документов на лицензирование Презентация на тему Изобразительное искусство классицизма и рококо
Презентация на тему Изобразительное искусство классицизма и рококо КИНЕШМА
КИНЕШМА Обработка нижнего среза изделия
Обработка нижнего среза изделия Педагогическая практика организации внеурочной и внеклассной деятельности
Педагогическая практика организации внеурочной и внеклассной деятельности Положение об общественном совете муниципального образования Северодвинск
Положение об общественном совете муниципального образования Северодвинск Луи , ПАСТЕР (Pasteur)
Луи , ПАСТЕР (Pasteur) Хохломская роспись
Хохломская роспись Горячая линия
Горячая линия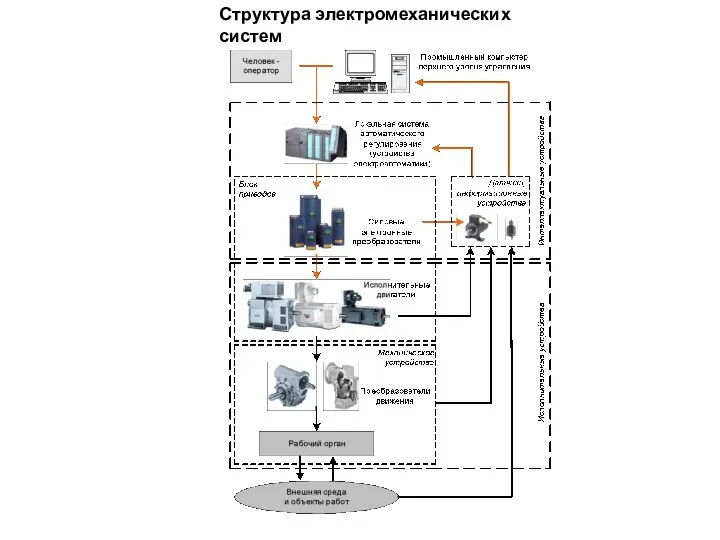 Структура электромеханических систем
Структура электромеханических систем Характер человека
Характер человека Преодоление сложностей при запоминании таблицы умножения
Преодоление сложностей при запоминании таблицы умножения Презентация на тему Юридическая клиника в кыргызско-российском славянском университете имени Бориса Ельцина
Презентация на тему Юридическая клиника в кыргызско-российском славянском университете имени Бориса Ельцина  Презентация на тему Военно-патриотическое воспитание
Презентация на тему Военно-патриотическое воспитание Обобщающий урок во 2 классе
Обобщающий урок во 2 классе Дистрибуция прессы в сети супермаркетов в России. Тенденции и перспективы развития.
Дистрибуция прессы в сети супермаркетов в России. Тенденции и перспективы развития. Использование 3D технологии в медицине
Использование 3D технологии в медицине Кружок робототехники
Кружок робототехники Война за независимость США
Война за независимость США Современная теория фотосинтеза
Современная теория фотосинтеза Программный комплекс «Карат» предназначен для создания в базе данных показателей любого типа, ручного ввода или автоматической п
Программный комплекс «Карат» предназначен для создания в базе данных показателей любого типа, ручного ввода или автоматической п Prezentacia_лекція_10-1_ТЕК (3)
Prezentacia_лекція_10-1_ТЕК (3)