Слайд 2 Построение линии взаимного пересечения двух многогранников состоит в следующем построении
1.

Строим точки пересечения ребер первого многогранника с гранями второго многогранника. Каждое ребро представляет собой прямую, которое пересекает ребро второго многогранника в точке пересечения.
2. Пересечение ребер двух многогранников следует рассматривать как пересечение двух прямых.
3. Линию пересечения двух граней следует рассматривать как линию пересечения двух плоскостей.
Построение линии взаимного пересечения поверхностей двух призм является самым простым .
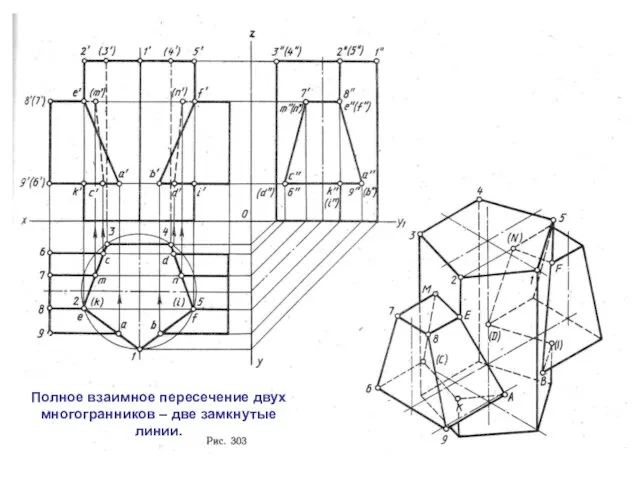
Слайд 3Полное взаимное пересечение двух многогранников – две замкнутые линии.
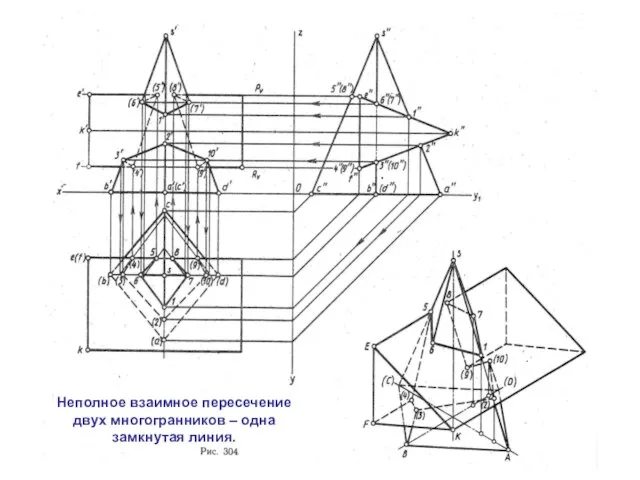
Слайд 4Неполное взаимное пересечение
двух многогранников – одна
замкнутая линия.
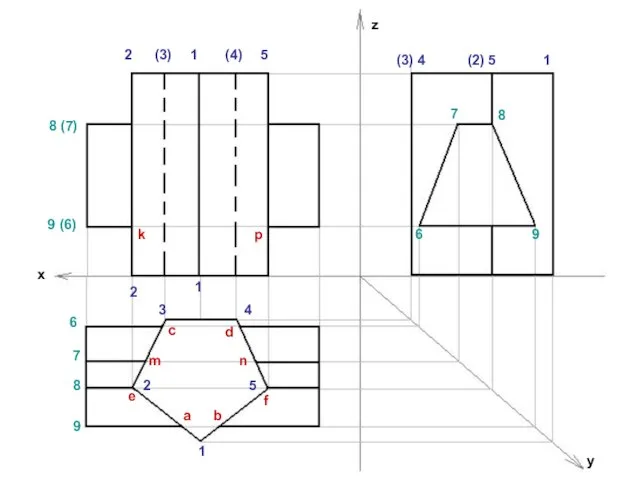
Слайд 5y
x
z
1
2
3
4
5
2
2
(3)
1
(4)
1
5
1
(3) 4
(2) 5
6
7
8
9
8 (7)
9 (6)
7
8
6
9
a
b
c
d
m
n
e
f
p
k
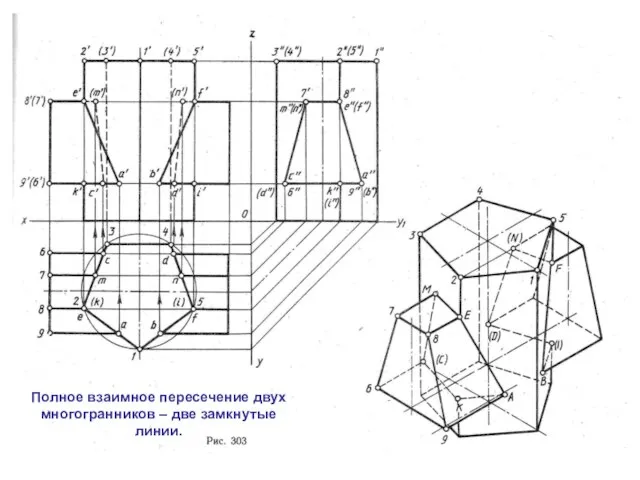
Слайд 7Полное взаимное пересечение двух многогранников – две замкнутые линии.
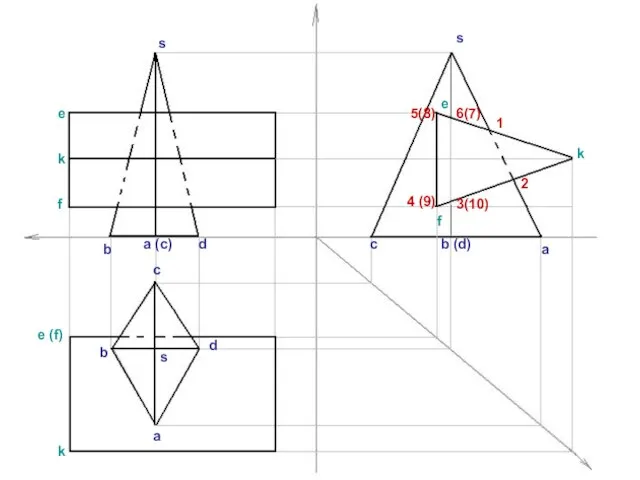
Слайд 8s
s
s
a
b
c
d
b
a (c)
d
c
a
b (d)
k
e (f)
e
k
f
e
k
f
1
2
3(10)
4 (9)
6(7)
5(8)
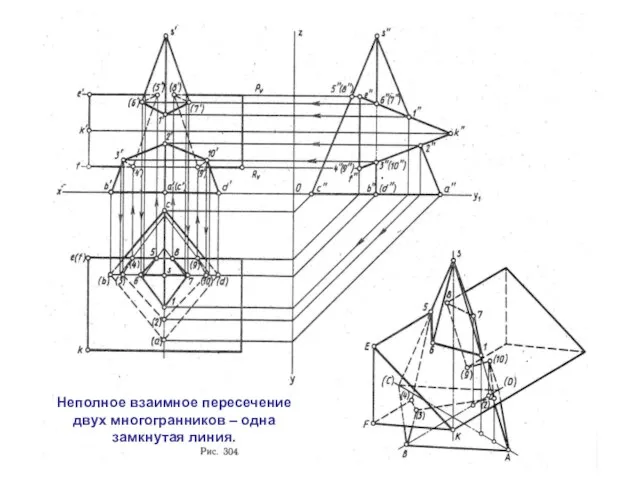
Слайд 10Неполное взаимное пересечение
двух многогранников – одна
замкнутая линия.







 GENTLE DAY
GENTLE DAY Экваториальные леса Южной Америки
Экваториальные леса Южной Америки Презентация на тему Рыцарство и его культура
Презентация на тему Рыцарство и его культура  Что такое голография?
Что такое голография? Кодекс 4ести Яно4ки
Кодекс 4ести Яно4ки Презентация _Религия в советский период_
Презентация _Религия в советский период_ Анкетирование по мотивации
Анкетирование по мотивации Сторителлинг: как написать смешную шутку
Сторителлинг: как написать смешную шутку Презентация на тему Полимеразная цепная реакция
Презентация на тему Полимеразная цепная реакция Пусковые процессы и стационарный режим работы мостового выпрямителя
Пусковые процессы и стационарный режим работы мостового выпрямителя Laboratory for Internet studies
Laboratory for Internet studies Заключение трудового договора о дистанционной работе с сотрудником, проживающим за рубежом
Заключение трудового договора о дистанционной работе с сотрудником, проживающим за рубежом Чемпионат и Первенство России 2020. Г. Казань
Чемпионат и Первенство России 2020. Г. Казань Презентация на тему Условный выпуск товаров таможенными органами
Презентация на тему Условный выпуск товаров таможенными органами  Учебный семинар От «новых стандартов» к инновационной деятельности педагогов школы.
Учебный семинар От «новых стандартов» к инновационной деятельности педагогов школы. Douglas DC-3
Douglas DC-3 Импрессионизм. Практическая работа
Импрессионизм. Практическая работа ЧТО ТАКОЕЛИДЕРСТВО?
ЧТО ТАКОЕЛИДЕРСТВО? Межпредметная интеграция – главный ресурс качества образования
Межпредметная интеграция – главный ресурс качества образования Конкуренция и монополия Виды конкуренции
Конкуренция и монополия Виды конкуренции Конституция России
Конституция России Нитьи Лалиты
Нитьи Лалиты Презентация на тему Исчисляемые и неисчисляемые существительные
Презентация на тему Исчисляемые и неисчисляемые существительные Museo de Louvre
Museo de Louvre ООО Тринити-К. Летняя практика
ООО Тринити-К. Летняя практика Знаешь ли ты географию своей страны?
Знаешь ли ты географию своей страны? Гимнастика. Виды
Гимнастика. Виды editdocument16648092075845 (1)
editdocument16648092075845 (1)