Построение мероморфных функций на накрытиях Римановых поверхностей векторных задач дискретной оптимизации.

Структура работы
Актуальность
Цели и задачи
Определение и примеры римановых поверхностей
Мероморфные функции и их свойства
Пример построения мероморфной функции
Заключение
Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»

Актуальность
Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»
Проблема нахождения мероморфных функций является центральной в теории функции на римановых поверхностях. В настоящее время известны многочисленные теоремы существований мероморфных функций с различными особенностями. Однако эти теоремы не решают проблему нахождения аналитических выражений для мероморфных функций.

Цели и задачи
Исследование римановых поверхностей и их свойств;
Построение мероморфных функций на накрытиях римановых поверхностей;
Практическая реализация рассмотренных примеров и задач.
Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»

Определение римановых поверхностей
Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»
Пусть Х – двухмерное многообразие (n-мерным многообразием называется хаусдорфово пространство Х, каждая точка которого обладает окрестностью, гомеоморфной некоторому открытому подмножеству в ).
Комплексной структурой на двухмерном многообразии Х называется класс эквивалентности биголоморфно согласованных атласов на Х.
Риманова поверхность – это пара .

Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»
Примеры римановых поверхностей
Гауссова числовая плоскость С.
Риманова числовая сфера
Торы.
Риманова поверхность корня.
Риманова поверхность
алгебраических функций.

Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»
Мероморфные функции
и их свойства
Пусть Х – риманова поверхность и Y – открытое подмножество Х.
Мероморфной функцией на Y называется аналитическая функция , определенная на открытом подмножестве со следующими
свойствами:
1. состоит только из изолированных точек;
2. для каждой точки имеем: .
Точки множества называются полюсами
функции f.

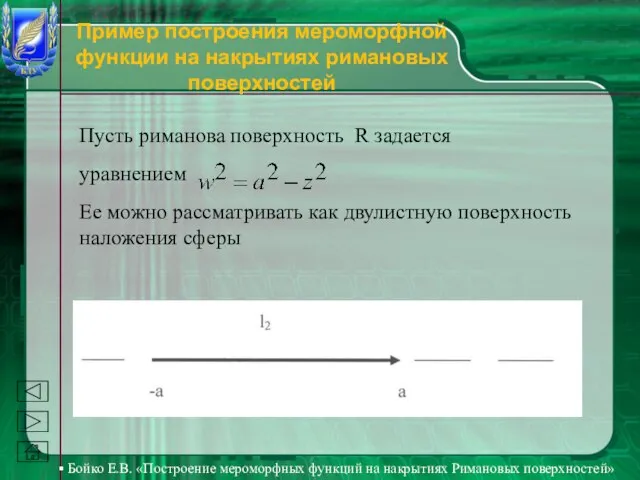
Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»
Пример построения мероморфной функции на накрытиях римановых поверхностей
Пусть риманова поверхность R задается
уравнением
Ее можно рассматривать как двулистную поверхность наложения сферы

Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»
…
Подстановка на разрезе . Возьмем два экземпляра поверхности R, разрежем вдоль прямых, лежащих над
и «склеим» два таких экземпляра «крест-накрест». В результате получится четырёхлистная поверхность наложения сферы со следующими подстановками.
На разрезе
На разрезах

Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»
…
Находим поле мероморфных функций на R.

Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»
В качестве решения будем искать вектор-функцию, порядок роста которой следующий
Найдем матрицу N, осуществляющую одновременную диагонализацию матриц C и D, и перепишем для вектор- функции в виде:
…

Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»
…
Из асимптотики для w(z) получим асимптотику для функции Ф(z):
Выделяя координаты в неравенствах, получим требуемые скалярные задачи Римана на плоскости. Учитывая асимптотику запишем решение:

Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»
…
Возвращаемся к функции и учитывая найденные константы
получаем искомое решение задачи:

Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»
…
В итоге получаем:

Заключение
Рассмотрены различные подходы к определению римановых поверхностей.
Дано определение накрытий римановых поверхностей.
Построена мероморфная функция на накрытиях римановых поверхностей.
Бойко Е.В. «Построение мероморфных функций на накрытиях Римановых поверхностей»