Построение сечений многогранников

Существуют проблемы при изучении стереометрии. Формальные знания по этому разделу школьной математики обнаруживаются у большинства учащихся: недостаточно сформированное пространственное представление учащихся, отсутствие умения выполнять проекционный чертёж и оперировать данными на нем. Изучение темы «Построение сечений многогранников» предполагает устойчивое развитие пространственного воображения учащихся необходимое для свободного овладения умением решать стереометрические задачи. Он знакомит учащихся с понятием поэтапного построения на проекционном чертеже. В школьном курсе стереометрии на тему: «Построение сечений» отводится всего два часа. Программа приведенного ниже элективного курса предполагает ознакомление с основными методами решения задач на построение сечений многогранников, применение которых способствует осознанию учащимися поэтапного построения сечения многогранника, формирует основы грамотного построения моделей многогранников, развивает пространственное представление и воображение учащихся. Данный курс призван помочь учителям средней школы в решении следующих образовательных задач:
- обучение учащихся методам построения (изображения) пространственных фигур на плоскости;
- обучение учащихся методам решения задач на построение сечений многогранников.

Программа элективного курса для 10-го класса (I вариант)

Программа элективного курса для 10-го класса (II вариант)

Цели элективного курса
формирование основ научного мировоззрения, базирующегося на инвариантных и фундаментальных знаниях стереометрии;
формирование основ грамотного построения моделей многогранников;
развитие пространственных представлений и воображения учащихся;
выявление и развитие математических способностей учащихся.

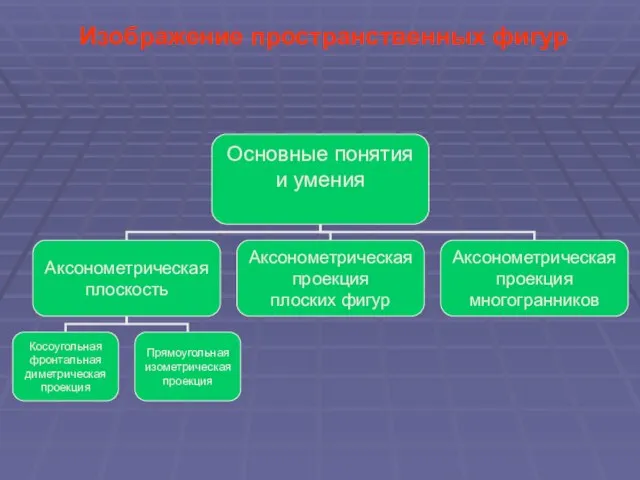
Изображение пространственных фигур

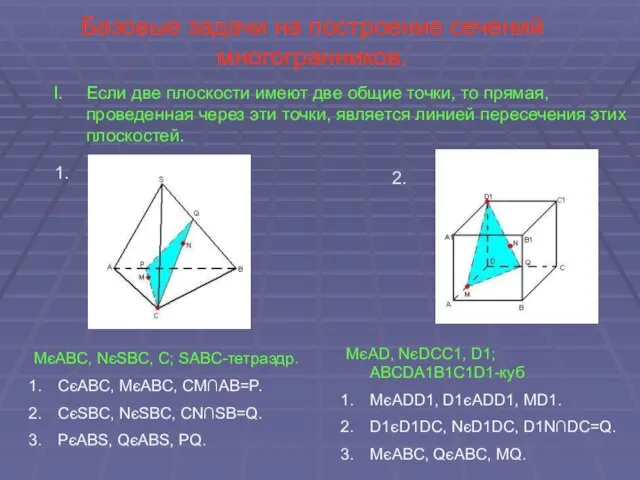
Базовые задачи на построение сечений многогранников.
Если две плоскости имеют две общие точки, то прямая, проведенная через эти точки, является линией пересечения этих плоскостей.
1.
2.
MєABC, NєSBC, C; SABC-тетраэдр.
CєABC, MєABC, CM∩AB=P.
CєSBC, NєSBC, CN∩SB=Q.
PєABS, QєABS, PQ.
MєAD, NєDCC1, D1; ABCDA1B1C1D1-куб
MєADD1, D1єADD1, MD1.
D1єD1DC, NєD1DC, D1N∩DC=Q.
MєABC, QєABC, MQ.

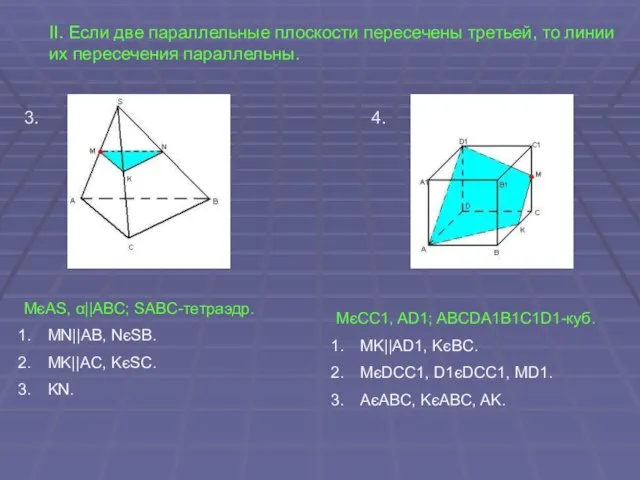
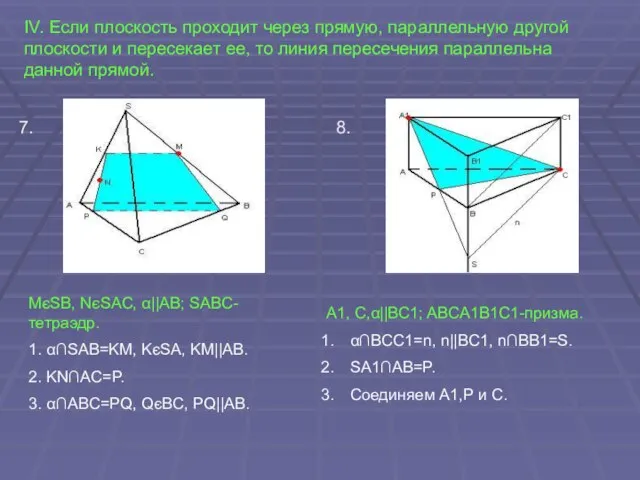
II. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
3.
4.
MєAS, α||ABC; SABC-тетраэдр.
MN||AB, NєSB.
MK||AC, KєSC.
KN.
MєCC1, AD1; ABCDA1B1C1D1-куб.
MK||AD1, KєBC.
MєDCC1, D1єDCC1, MD1.
AєABC, KєABC, AK.

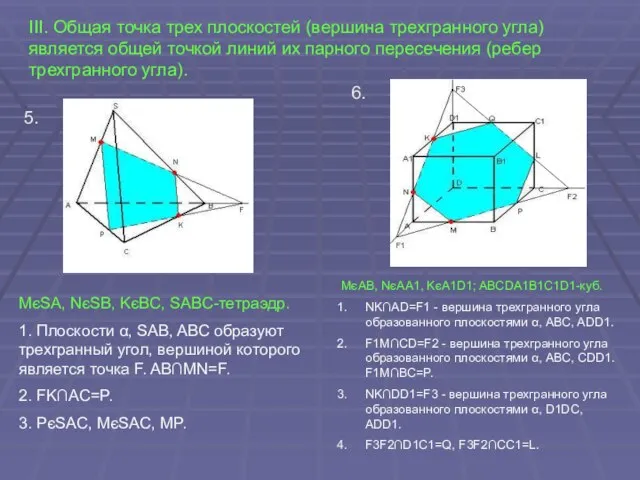
III. Общая точка трех плоскостей (вершина трехгранного угла) является общей точкой линий их парного пересечения (ребер трехгранного угла).
5.
6.
MєSA, NєSB, KєBC, SABC-тетраэдр.
1. Плоскости α, SAB, ABC образуют трехгранный угол, вершиной которого является точка F. AB∩MN=F.
2. FK∩AC=P.
3. PєSAC, MєSAC, MP.
MєAB, NєAA1, KєA1D1; ABCDA1B1C1D1-куб.
NK∩AD=F1 - вершина трехгранного угла образованного плоскостями α, ABC, ADD1.
F1M∩CD=F2 - вершина трехгранного угла образованного плоскостями α, ABC, CDD1. F1M∩BC=P.
NK∩DD1=F3 - вершина трехгранного угла образованного плоскостями α, D1DC, ADD1.
F3F2∩D1C1=Q, F3F2∩CC1=L.

IV. Если плоскость проходит через прямую, параллельную другой плоскости и пересекает ее, то линия пересечения параллельна данной прямой.
7.
8.
MєSB, NєSAC, α||AB; SABC-тетраэдр.
1. α∩SAB=KM, KєSA, KM||AB.
2. KN∩AC=P.
3. α∩ABC=PQ, QєBC, PQ||AB.
A1, C,α||BC1; ABCA1B1C1-призма.
α∩BCC1=n, n||BC1, n∩BB1=S.
SA1∩AB=P.
Соединяем A1,P и C.

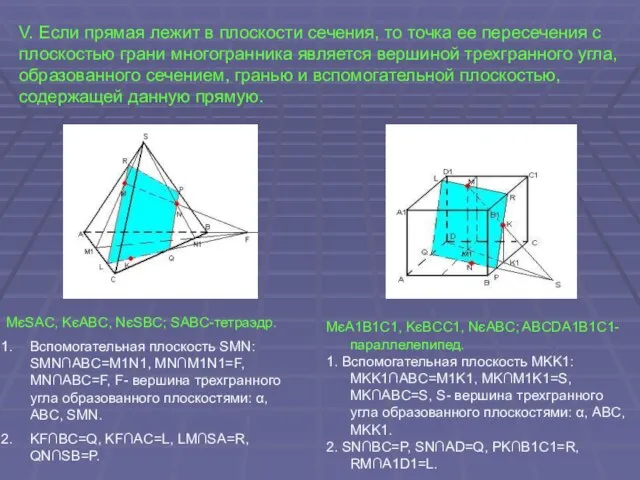
V. Если прямая лежит в плоскости сечения, то точка ее пересечения с плоскостью грани многогранника является вершиной трехгранного угла, образованного сечением, гранью и вспомогательной плоскостью, содержащей данную прямую.
MєSAC, KєABC, NєSBC; SABC-тетраэдр.
Вспомогательная плоскость SMN: SMN∩ABC=M1N1, MN∩M1N1=F, MN∩ABC=F, F- вершина трехгранного угла образованного плоскостями: α, ABC, SMN.
KF∩BC=Q, KF∩AC=L, LM∩SA=R, QN∩SB=P.
MєA1B1C1, KєBCC1, NєABC; ABCDA1B1C1-параллелепипед.
1. Вспомогательная плоскость MKK1: MKK1∩ABC=M1K1, MK∩M1K1=S, MK∩ABC=S, S- вершина трехгранного угла образованного плоскостями: α, ABC, MKK1.
2. SN∩BC=P, SN∩AD=Q, PK∩B1C1=R, RM∩A1D1=L.

Правило для самоконтроля.
Если многогранник выпуклый, то сечение выпуклый многоугольник.
Вершины многоугольника всегда лежат на ребрах многогранника.
Если точки сечения лежат на ребрах многогранника, то они являются вершинами многоугольника, который получится в сечении.
Если точки сечения лежат на гранях многогранника, то они лежат на сторонах многоугольника, который получится в сечении.
Две стороны многоугольника, который получится в сечении, не могут принадлежать одной грани многогранника.
Если сечение пересекает две параллельные грани, то и отрезки (стороны многоугольника, который получится в сечении) будут параллельны.

Построение сечения методом следов
Для объяснения материала учителю необходимо заготовить:
набор листов с заданиями и рисунками (для экономии времени урока);
аналогичные чертежи и таблицы на доске или компьютере.

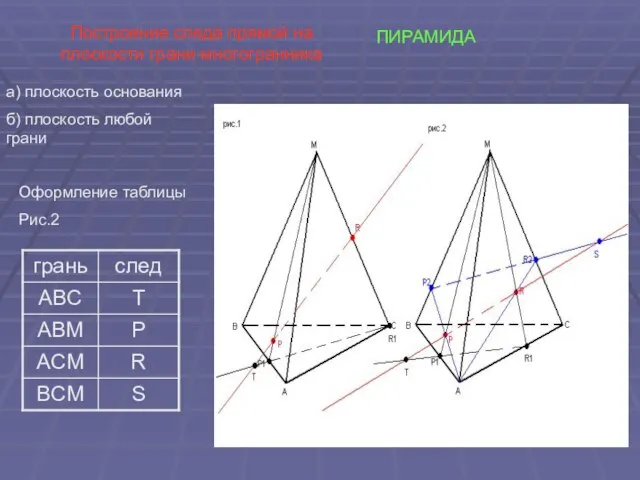
ПИРАМИДА
Построение следа прямой на плоскости грани многогранника
а) плоскость основания
б) плоскость любой грани
Оформление таблицы
Рис.2

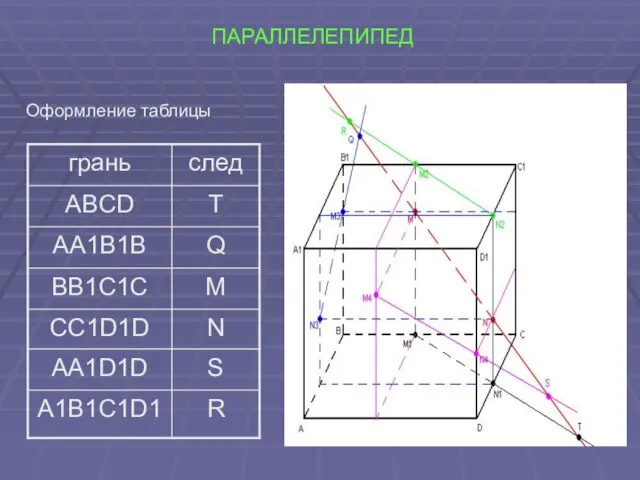
ПАРАЛЛЕЛЕПИПЕД
Оформление таблицы

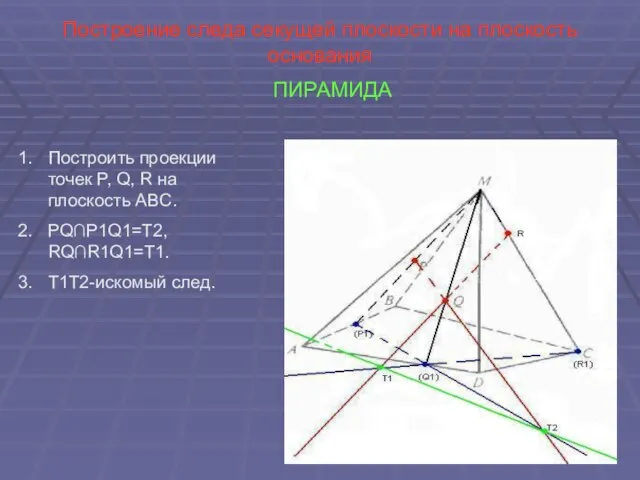
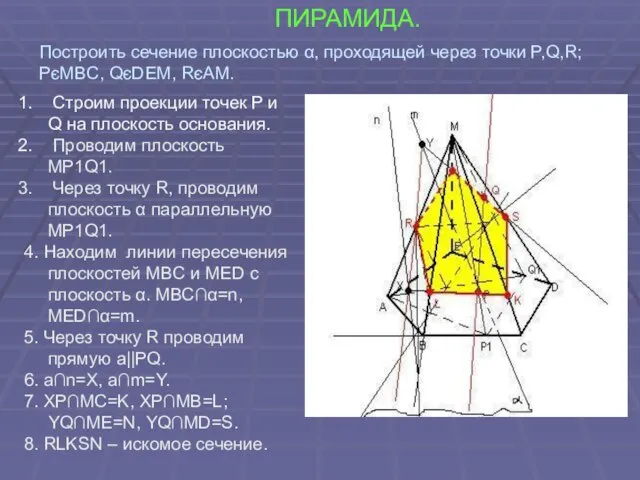
Построение следа секущей плоскости на плоскость основания
ПИРАМИДА
Построить проекции точек P, Q, R на плоскость ABC.
PQ∩P1Q1=T2, RQ∩R1Q1=T1.
T1T2-искомый след.

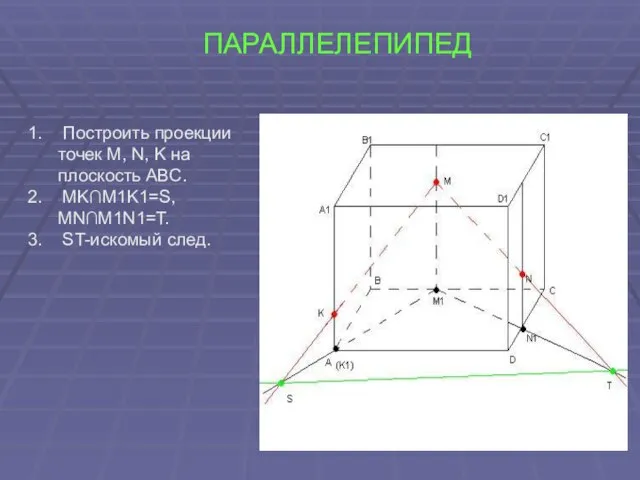
ПАРАЛЛЕЛЕПИПЕД
Построить проекции точек M, N, K на плоскость ABC.
MK∩M1K1=S, MN∩M1N1=T. ST-искомый след.

Алгоритм построения
сечения методом следов
Выяснить имеются ли в одной грани две точки сечения (если да, то через них можно провести сторону сечения).
Построить след сечения на плоскости основания многогранника.
Найти дополнительную точку сечения на ребре многогранника (продолжить сторону основания той грани, в которой есть точка сечения, до пересечения со следом).
Через полученную дополнительную точку на следе и точку сечения в выбранной грани провести прямую, отметить точки пересечения её с рёбрами грани.
Выполнить п.1.

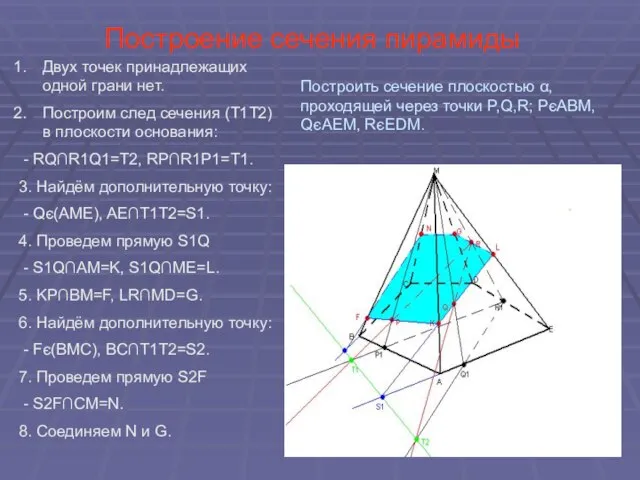
Построение сечения пирамиды
Двух точек принадлежащих одной грани нет.
Построим след сечения (Т1Т2) в плоскости основания:
- RQ∩R1Q1=T2, RP∩R1P1=T1.
3. Найдём дополнительную точку:
- Qє(AME), AE∩T1T2=S1.
4. Проведем прямую S1Q
- S1Q∩AM=K, S1Q∩ME=L.
5. KP∩BM=F, LR∩MD=G.
6. Найдём дополнительную точку:
- Fє(BMC), BC∩T1T2=S2.
7. Проведем прямую S2F
- S2F∩CM=N.
8. Соединяем N и G.
Построить сечение плоскостью α, проходящей через точки P,Q,R; PєABM, QєAEM, RєEDM.

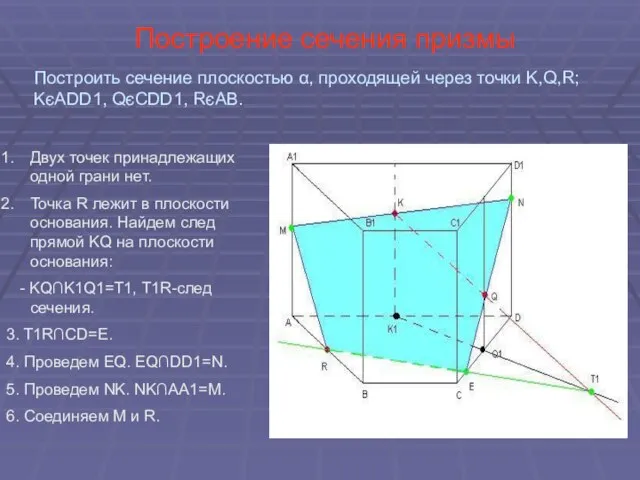
Построение сечения призмы
Двух точек принадлежащих одной грани нет.
Точка R лежит в плоскости основания. Найдем след прямой KQ на плоскости основания:
- KQ∩K1Q1=T1, T1R-след сечения.
3. T1R∩CD=E.
4. Проведем EQ. EQ∩DD1=N.
5. Проведем NK. NK∩AA1=M.
6. Соединяем M и R.
Построить сечение плоскостью α, проходящей через точки K,Q,R; KєADD1, QєCDD1, RєAB.

Построение сечения методом
внутреннего проектирования.
Этот метод является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь в виду, что построения, выполняемые при использовании этого метода, зачастую получаются «скученными». Тем не менее в некоторых случаях метод внутреннего проектирования оказывается наиболее рациональным.

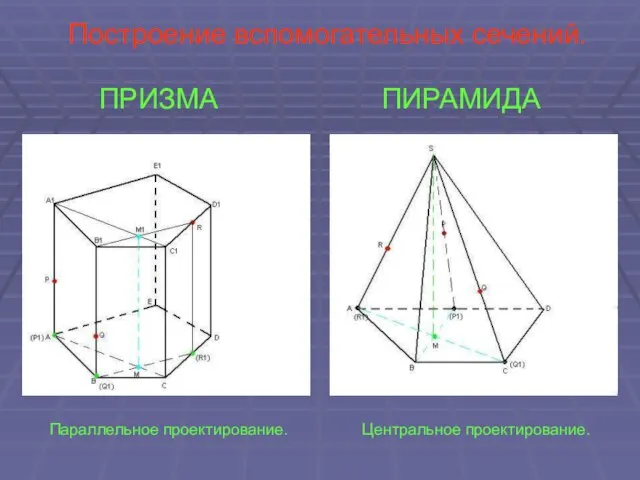
Построение вспомогательных сечений.
ПРИЗМА
ПИРАМИДА
Параллельное проектирование.
Центральное проектирование.

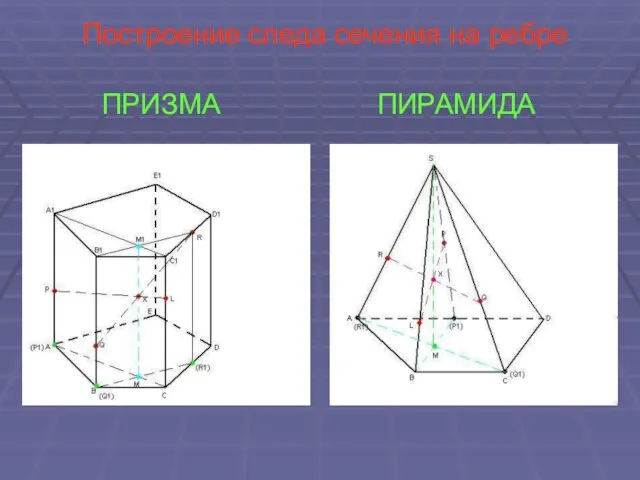
Построение следа сечения на ребре
ПРИЗМА
ПИРАМИДА

Алгоритм построения сечения методом
внутреннего проектирования.
Построить вспомогательные сечения и найти линию их пересечения.
Построить след сечения на ребре многогранника.
Если точек сечения не хватает для построения самого сечения повторить пп.1-2.

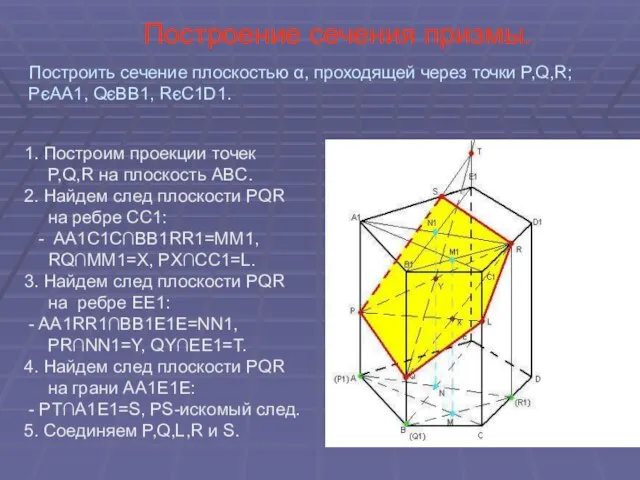
Построение сечения призмы.
1. Построим проекции точек P,Q,R на плоскость ABC.
2. Найдем след плоскости PQR на ребре CC1:
- AA1C1C∩BB1RR1=MM1, RQ∩MM1=X, PX∩CC1=L.
3. Найдем след плоскости PQR на ребре EE1:
- AA1RR1∩BB1E1E=NN1, PR∩NN1=Y, QY∩EE1=T.
4. Найдем след плоскости PQR на грани AA1E1E:
- PT∩A1E1=S, PS-искомый след.
5. Соединяем P,Q,L,R и S.
Построить сечение плоскостью α, проходящей через точки P,Q,R; PєAA1, QєBB1, RєC1D1.

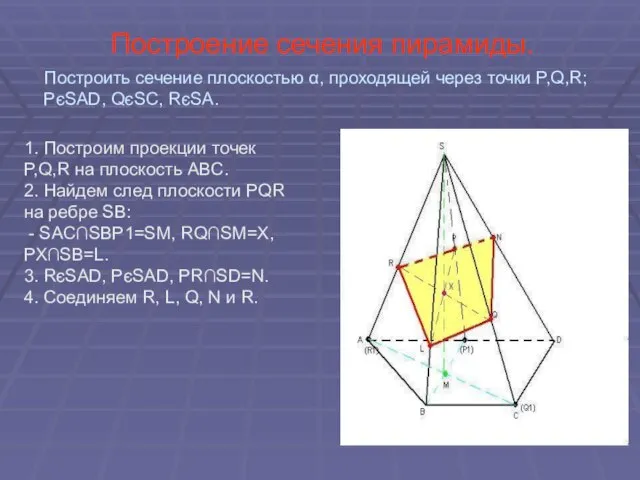
Построение сечения пирамиды.
1. Построим проекции точек P,Q,R на плоскость ABC.
2. Найдем след плоскости PQR на ребре SB:
- SAC∩SBP1=SM, RQ∩SM=X, PX∩SB=L.
3. RєSAD, PєSAD, PR∩SD=N.
4. Соединяем R, L, Q, N и R.
Построить сечение плоскостью α, проходящей через точки P,Q,R; PєSAD, QєSC, RєSA.

Метод дополнения n-угольной призмы(пирамиды) до треугольной призмы(пирамиды).
Данная призма(пирамида) достраивается до треугольной призмы(пирамиды) из тех граней на боковых ребрах или гранях которой лежат точки, определяющие искомое сечение.
Строится сечение полученной треугольной призмы(пирамиды).
Искомое сечение получается как часть сечения треугольной призмы(пирамиды).

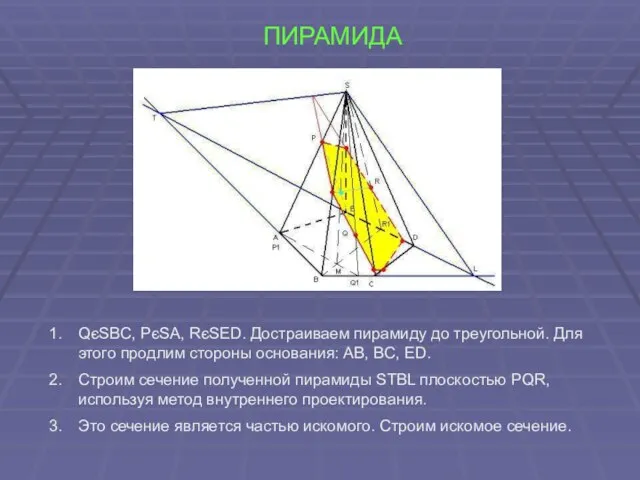
ПИРАМИДА
QєSBC, PєSA, RєSED. Достраиваем пирамиду до треугольной. Для этого продлим стороны основания: AB, BC, ED.
Строим сечение полученной пирамиды STBL плоскостью PQR, используя метод внутреннего проектирования.
Это сечение является частью искомого. Строим искомое сечение.

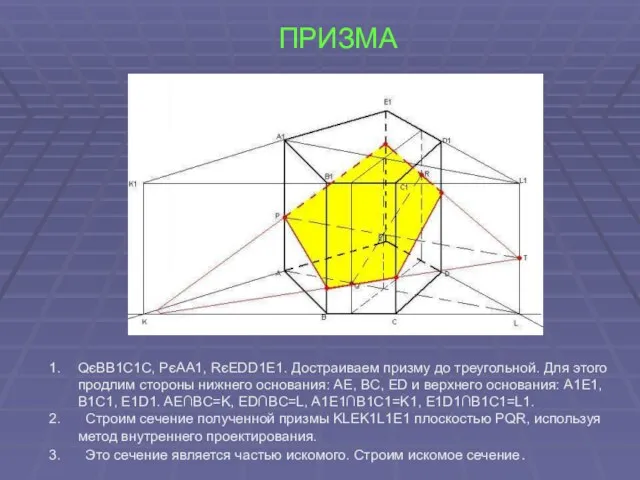
ПРИЗМА
QєBB1C1C, PєAA1, RєEDD1E1. Достраиваем призму до треугольной. Для этого продлим стороны нижнего основания: AE, BC, ED и верхнего основания: A1E1, B1C1, E1D1. AE∩BC=K, ED∩BC=L, A1E1∩B1C1=K1, E1D1∩B1C1=L1.
Строим сечение полученной призмы KLEK1L1E1 плоскостью PQR, используя метод внутреннего проектирования.
Это сечение является частью искомого. Строим искомое сечение.

Метод деления n-угольной призмы(пирамиды) на треугольные призмы(пирамиды).
Строим проекции точек на плоскость основания.
Из данной призмы(пирамиды) выделяется та треугольная призма(пирамида) на боковых ребрах или гранях которой лежат точки, определяющие искомое сечение.
В выделенной призме(пирамиде) точки, определяющие искомое сечение должны лежать на ребрах.
Строится сечение этой треугольной призмы(пирамиды).

5. Данная призма(пирамида) разбивается на треугольные призмы(пирамиды), таким образом, что одна из граней должна пересечь две грани выделенной призмы(пирамиды).
6. Находим линии пересечения этих граней. Эти линии пересекут стороны построенного сечения в двух точках, которые принадлежат искомому сечению и грани призмы (пирамиды).
7. Находим точки пересечения с боковыми ребрами призмы(пирамиды).
8. Строим искомое сечение.

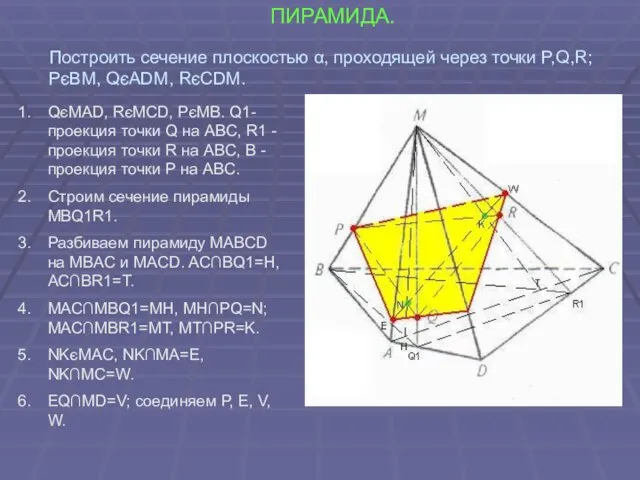
ПИРАМИДА.
QєMAD, RєMCD, PєMB. Q1-проекция точки Q на ABC, R1 -проекция точки R на ABC, B -проекция точки P на ABC.
Строим сечение пирамиды MBQ1R1.
Разбиваем пирамиду MABCD на MBAC и MACD. AC∩BQ1=H, AC∩BR1=T.
MAC∩MBQ1=MH, MH∩PQ=N; MAC∩MBR1=MT, MT∩PR=K.
NKєMAC, NK∩MA=E, NK∩MC=W.
EQ∩MD=V; соединяем P, E, V, W.
Построить сечение плоскостью α, проходящей через точки P,Q,R; PєBM, QєADM, RєCDM.

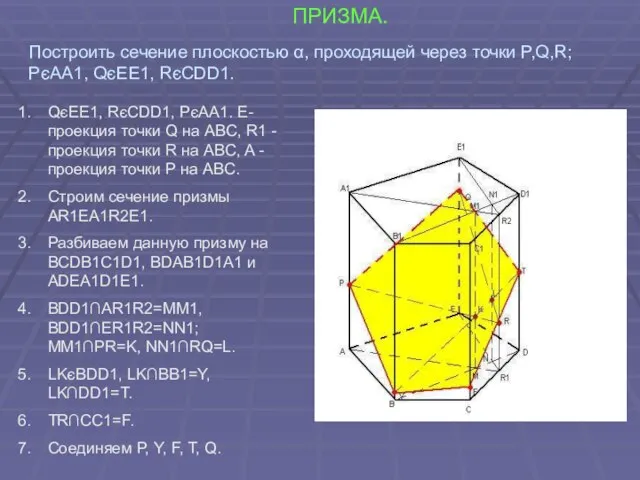
ПРИЗМА.
QєEE1, RєCDD1, PєAA1. E-проекция точки Q на ABC, R1 -проекция точки R на ABC, A -проекция точки P на ABC.
Строим сечение призмы AR1EA1R2E1.
Разбиваем данную призму на BCDB1C1D1, BDAB1D1A1 и ADEA1D1E1.
BDD1∩AR1R2=MM1, BDD1∩ER1R2=NN1; MM1∩PR=K, NN1∩RQ=L.
LKєBDD1, LK∩BB1=Y, LK∩DD1=T.
TR∩CC1=F.
Соединяем P, Y, F, T, Q.
Построить сечение плоскостью α, проходящей через точки P,Q,R; PєAA1, QєEE1, RєCDD1.

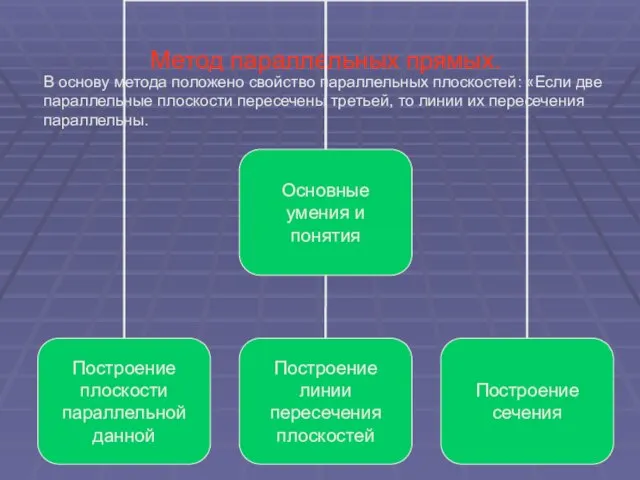
Метод параллельных прямых.
В основу метода положено свойство параллельных плоскостей: «Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

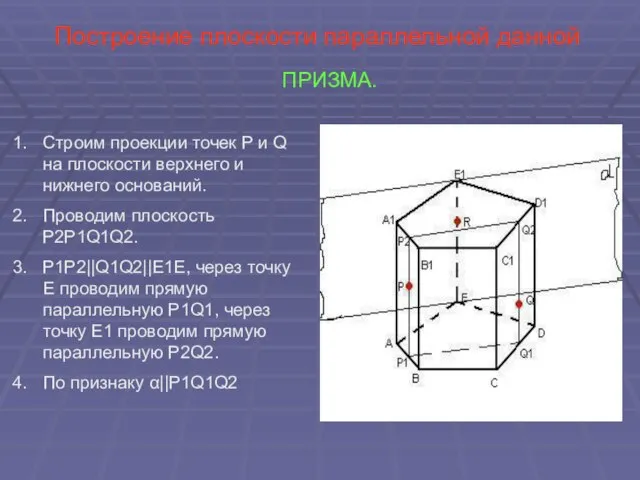
Построение плоскости параллельной данной
ПРИЗМА.
Строим проекции точек P и Q на плоскости верхнего и нижнего оснований.
Проводим плоскость P2P1Q1Q2.
P1P2||Q1Q2||E1E, через точку Е проводим прямую параллельную P1Q1, через точку Е1 проводим прямую параллельную P2Q2.
По признаку α||P1Q1Q2

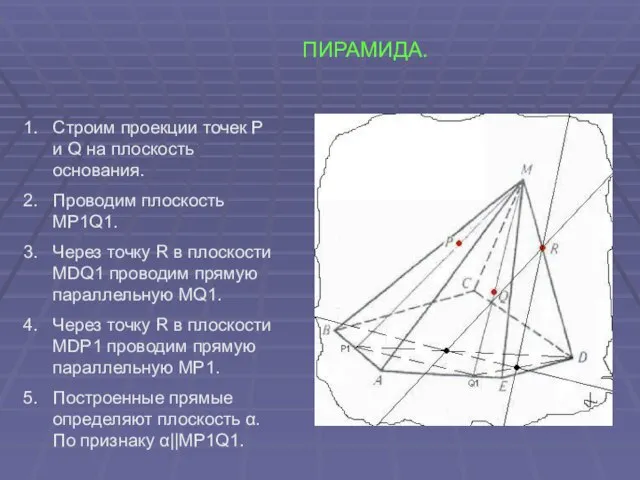
ПИРАМИДА.
Строим проекции точек P и Q на плоскость основания.
Проводим плоскость MP1Q1.
Через точку R в плоскости MDQ1 проводим прямую параллельную MQ1.
Через точку R в плоскости MDР1 проводим прямую параллельную MР1.
Построенные прямые определяют плоскость α. По признаку α||MP1Q1.

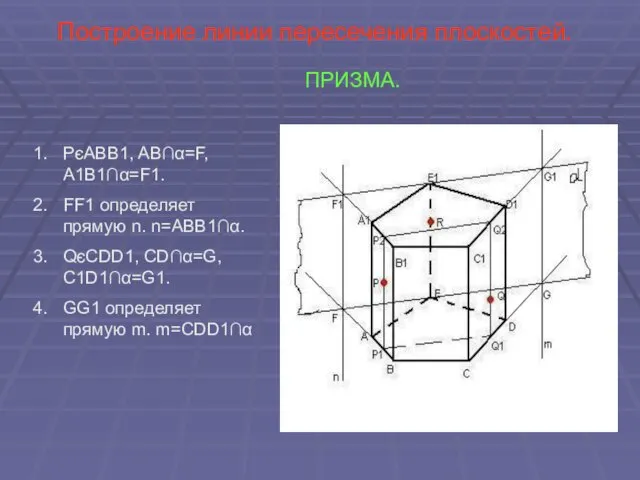
Построение линии пересечения плоскостей.
ПРИЗМА.
PєABB1, AB∩α=F, A1B1∩α=F1.
FF1 определяет прямую n. n=ABB1∩α.
QєCDD1, CD∩α=G, C1D1∩α=G1.
GG1 определяет прямую m. m=CDD1∩α

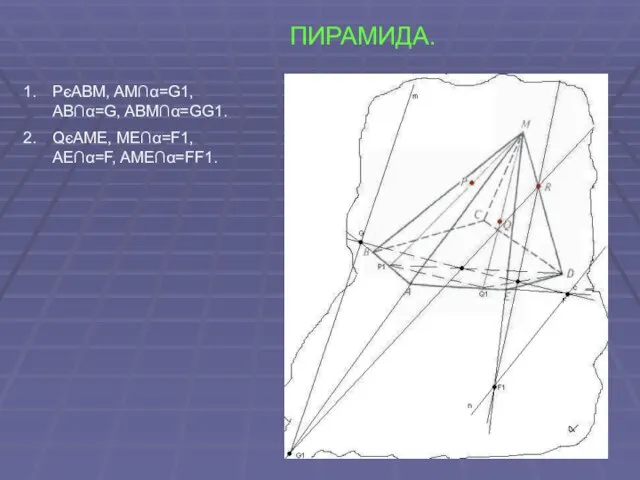
ПИРАМИДА.
PєABM, AM∩α=G1, AB∩α=G, ABM∩α=GG1.
QєAME, ME∩α=F1, AE∩α=F, AME∩α=FF1.

Алгоритм построения сечения
методом параллельных прямых.
Строим проекции точек, определяющих сечение. Через две данные точки (например P и Q) и их проекции проводим плоскость.
Через третью точку (например R) строим параллельную ей плоскость α.
Находим линии пересечения (например m и n) плоскости α с гранями многогранника содержащими точки P и Q.
Через точку R проводим прямую а параллельную PQ.
Находим точки пересечения прямой а с прямыми m и n.
Находим точки пересечения с ребрами соответствующей грани.

ПРИЗМА.
Строим проекции точек P и Q на плоскости верхнего и нижнего оснований.
Проводим плоскость P1Q1Q2P2.
Через ребро, содержащее точку R, проводим плоскость α параллельную P1Q1Q2.
Находим линии пересечения плоскостей ABB1и CDD1 с плоскость α.
Через точку R проводим прямуюa||PQ.
a∩n=X, a∩m=Y.
XP∩AA1=K, XP∩BB1=L; YQ∩CC1=M, YQ∩DD1=N.
KLMNR – искомое сечение.
Построить сечение плоскостью α, проходящей через точки P,Q,R; PєABB1, QєCDD1, RєEE1.

ПИРАМИДА.
Строим проекции точек P и Q на плоскость основания.
Проводим плоскость МP1Q1.
Через точку R, проводим плоскость α параллельную МP1Q1.
4. Находим линии пересечения плоскостей МBС и МЕD с плоскость α. МВС∩α=n, MED∩α=m.
5. Через точку R проводим прямую a||PQ.
6. a∩n=X, a∩m=Y.
7. XP∩MC=K, XP∩MB=L; YQ∩ME=N, YQ∩MD=S.
8. RLKSN – искомое сечение.
Построить сечение плоскостью α, проходящей через точки P,Q,R; PєMBC, QєDEM, RєAM.

Метод параллельного переноса секущей плоскости.
Строим вспомогательное сечение данного многогранника, которое удовлетворяет следующим требованиям: а) оно параллельно секущей плоскости; б) в пересечении с поверхностью данного многогранника образует треугольник.
Соединяем проекцию вершины треугольника с вершинами той грани многогранника, которую пересекает вспомогательное сечение, и находим точки пересечения со стороной треугольника, лежащей в этой грани.
Соединяем вершину треугольника с этими точками.
Через точку искомого сечения проводим прямые параллельные построенным отрезкам в предыдущем пункте и находим точки пересечения с ребрами многогранника.

ПРИЗМА.
RєAA1, PєEDD1, QєCDD1.Построим вспомогательное сечение AMQ1||RPQ. Проведем AM||RP, MQ1||PQ, AMQ1∩ABC=AQ1.
P1-проекция точек Р и М на АВС. Проведем Р1В и Р1С. Р1В∩AQ1=O1, P1C∩AQ1=O2.
Через точку Р проведем прямые m и n соответственно параллельные МО1 и МО2. m∩BB1=K, n∩CC1=L.
LQ∩DD1=T, TP∩EE1=S.
RKLTS –искомое сечение.
Построить сечение призмы плоскостью α, проходящей через точки P,Q,R; PєEDD1, QєCDD1, RєAA1.

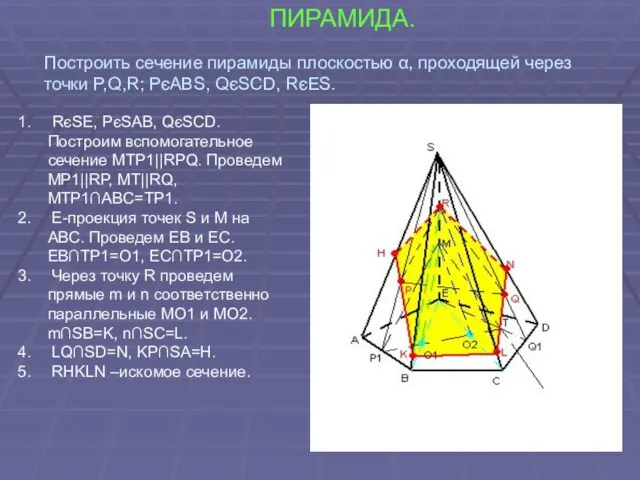
ПИРАМИДА.
RєSE, PєSAB, QєSCD. Построим вспомогательное сечение MTP1||RPQ. Проведем MP1||RP, MT||RQ, MTP1∩ABC=TP1. E-проекция точек S и М на АВС. Проведем EВ и EС. EВ∩TP1=O1, EC∩TP1=O2.
Через точку R проведем прямые m и n соответственно параллельные МО1 и МО2. m∩SB=K, n∩SC=L.
LQ∩SD=N, KP∩SA=H.
RHKLN –искомое сечение.
Построить сечение пирамиды плоскостью α, проходящей через точки P,Q,R; PєABS, QєSCD, RєES.

Комбинированный метод.
Через вторую прямую q и какую-нибудь точку W первой прямой р провести плоскость β.
В плоскости β через точку W провести прямую q‘ параллельную q.
Пересекающимися прямыми p и q‘ определяется плоскость α.
Непосредственное построение сечения многогранника плоскостью α
Суть метода состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом. Применяется для построения сечения многогранника с условием параллельности.
1. Построение сечения многогранника плоскостью α, проходящей через заданную прямую p параллельно другой заданной прямой q.

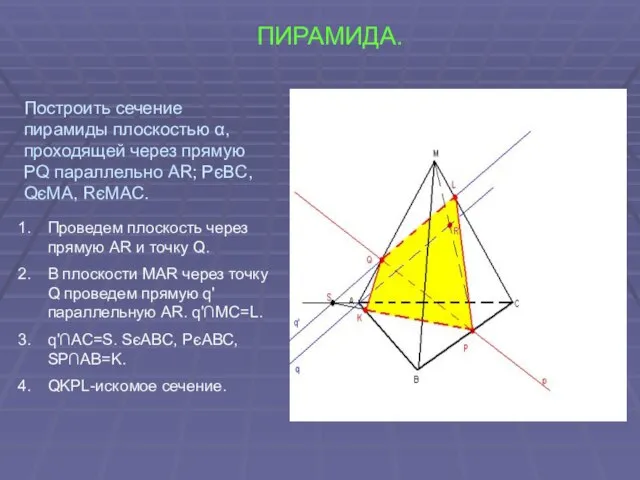
ПИРАМИДА.
Проведем плоскость через прямую AR и точку Q.
В плоскости MAR через точку Q проведем прямую q' параллельную AR. q'∩MC=L.
q'∩AC=S. SєABC, PєABC, SP∩AB=K.
QKPL-искомое сечение.
Построить сечение пирамиды плоскостью α, проходящей через прямую PQ параллельно AR; PєBC, QєMA, RєMAC.

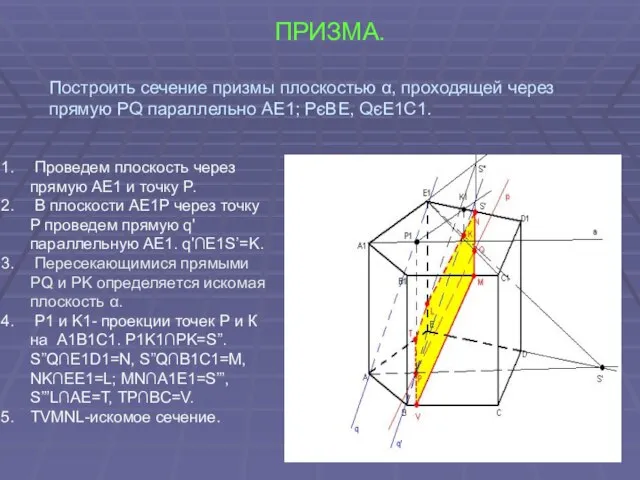
ПРИЗМА.
Построить сечение призмы плоскостью α, проходящей через прямую PQ параллельно AE1; PєBE, QєE1C1.
Проведем плоскость через прямую AE1 и точку P.
В плоскости AE1P через точку P проведем прямую q' параллельную AE1. q'∩E1S’=K.
Пересекающимися прямыми PQ и PK определяется искомая плоскость α.
P1 и K1- проекции точек Р и К на А1В1С1. P1K1∩PK=S”. S”Q∩E1D1=N, S”Q∩B1C1=M, NK∩EE1=L; MN∩A1E1=S”’, S”’L∩AE=T, TP∩BC=V.
TVMNL-искомое сечение.

2. Построение сечения многогранника плоскостью α, проходящей через заданную точку К параллельно двум заданным скрещивающимся прямым m и n.
Выбрать некоторую точку W. Эта точка может лежать на одной из заданных скрещивающихся прямых, может совпадать с точкой К.
Через точку W провести прямые n‘ и m‘. Если точка W лежит на одной из прямых, например на прямой n, то прямая n‘ совпадает с прямой n.
Пересекающимися прямыми n‘ и m‘ определяется плоскость β – плоскость вспомогательного сечения многогранника. Строим сечение многогранника плоскостью β.
Строим сечение многогранника плоскостью α, проходящей через точку К, параллельно плоскости β.

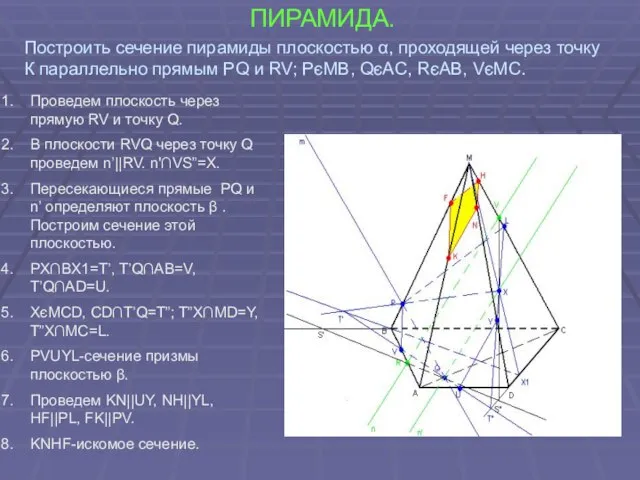
ПИРАМИДА.
Построить сечение пирамиды плоскостью α, проходящей через точку К параллельно прямым PQ и RV; PєMB, QєAC, RєAB, VєMC.
Проведем плоскость через прямую RV и точку Q.
В плоскости RVQ через точку Q проведем n’||RV. n'∩VS”=X.
Пересекающиеся прямые PQ и n’ определяют плоскость β . Построим сечение этой плоскостью.
PX∩BX1=T’, T’Q∩AB=V, T’Q∩AD=U.
XєMCD, CD∩T’Q=T”; T”X∩MD=Y, T”X∩MC=L.
PVUYL-сечение призмы плоскостью β.
Проведем KN||UY, NH||YL, HF||PL, FK||PV.
KNHF-искомое сечение.