Построение сечений многогранников

Определение сечения.
Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника.
Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

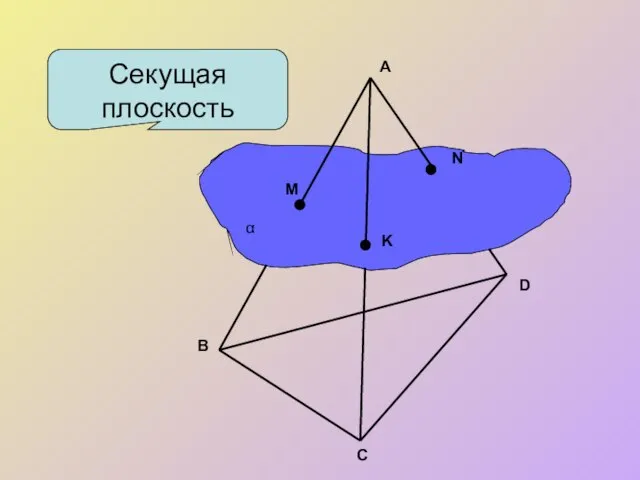
Секущая плоскость
А
В
С
D
M
N
K
α

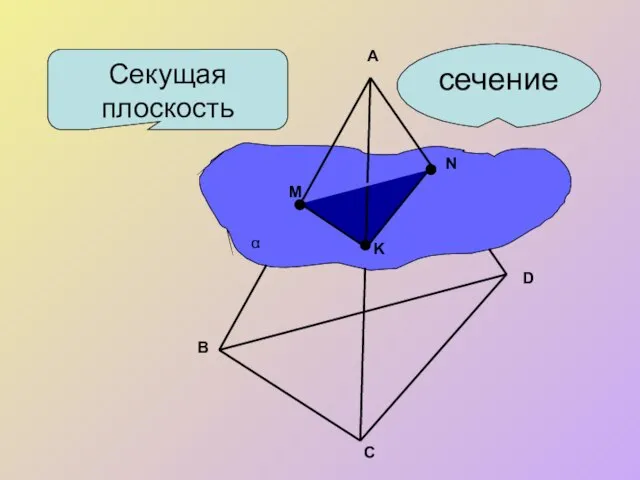
Секущая плоскость
сечение
A
B
C
D
M
N
K
α

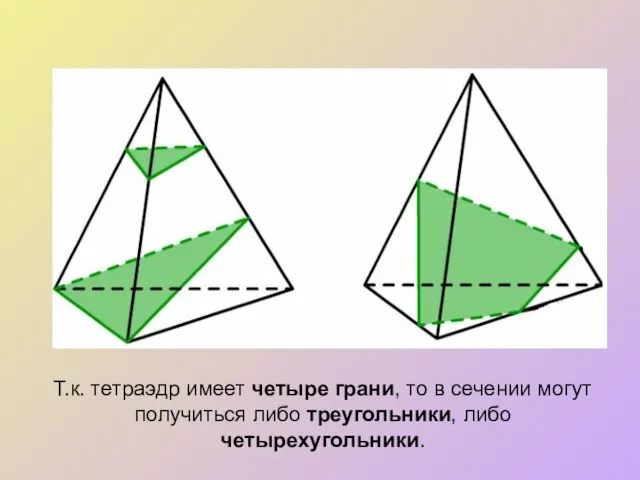
Т.к. тетраэдр имеет четыре грани, то в сечении могут получиться либо треугольники, либо четырехугольники.

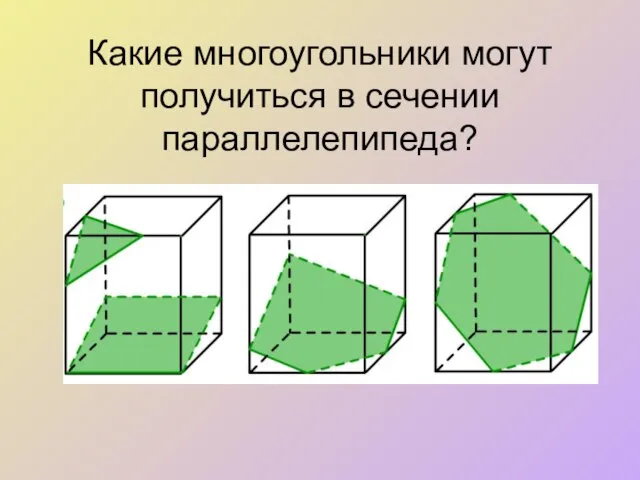
Какие многоугольники могут получиться в сечении параллелепипеда?

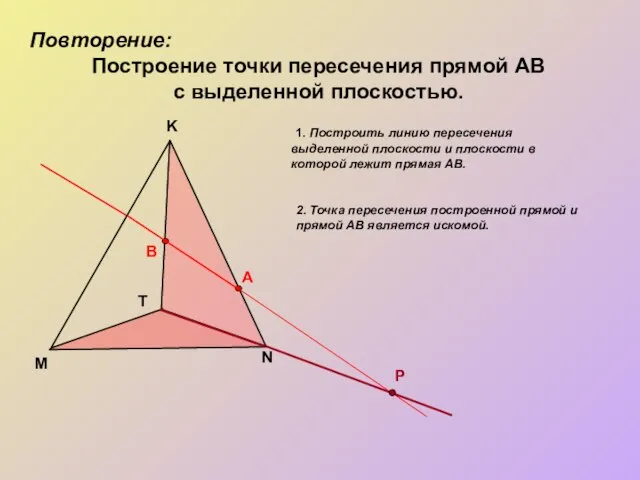
Повторение:
Построение точки пересечения прямой АВ
с выделенной плоскостью.
M
K
Т
A
B
1. Построить линию пересечения выделенной плоскости и плоскости в которой лежит прямая АВ.
2. Точка пересечения построенной прямой и прямой АВ является искомой.
N
Р

Задачи
на построение
сечений
тетраэдра и параллелепипеда

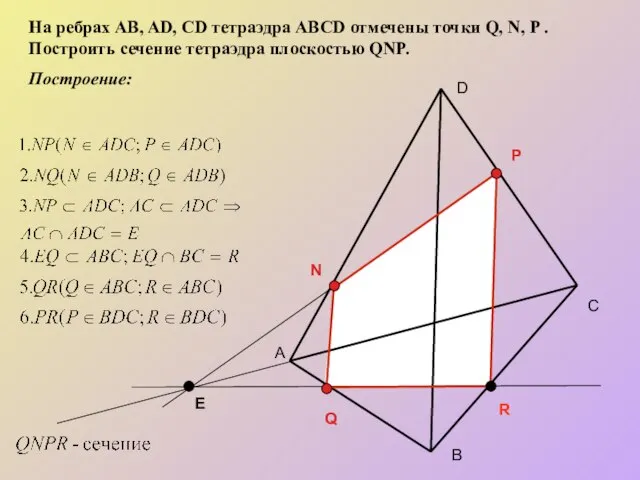
А
С
В
D
N
P
Q
R
На ребрах AB, AD, CD тетраэдра ABCD отмечены точки Q, N, P . Построить сечение тетраэдра плоскостью QNP.
Построение:
E

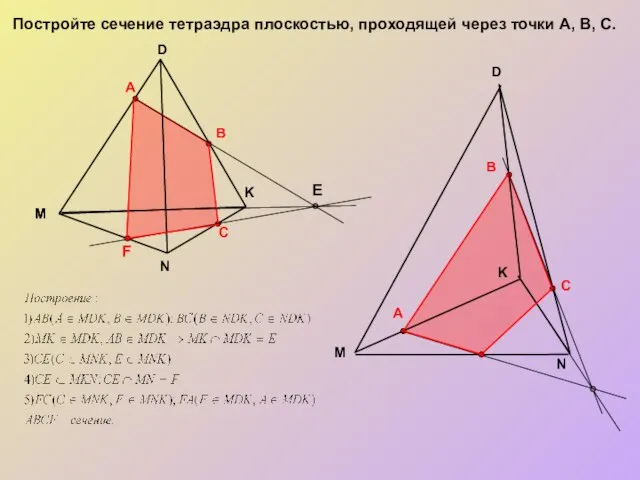
Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С.
M
K
A
B
M
N
C
D
M
N
K
D
B
C
A
Е
F

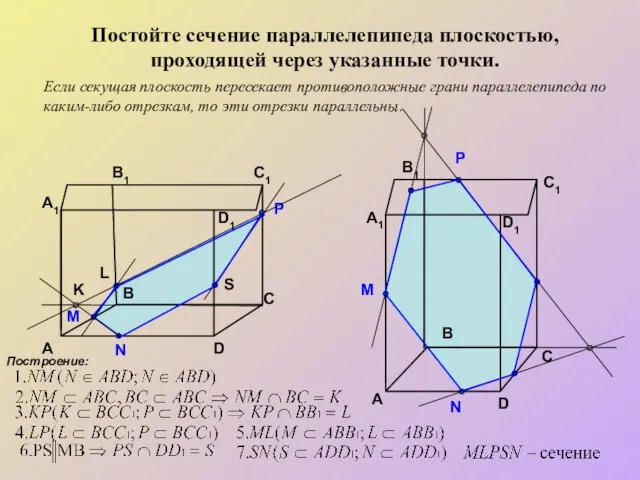
Постойте сечение параллелепипеда плоскостью, проходящей через указанные точки.
Если секущая плоскость пересекает противоположные грани параллелепипеда по каким-либо отрезкам, то эти отрезки параллельны.
S
L
K
Построение:

Построить точки пересечения секущей плоскости с рёбрами многогранника (тетраэдра, параллелепипеда).
2. Полученные точки, лежащие в одной грани, соединить отрезками.
3. Многоугольник, ограниченный данными отрезками, и есть построенное сечение.
Замечание: Если секущая плоскость пересекает противоположные грани параллелепипеда по каким-либо отрезкам, то эти отрезки параллельны.
Алгоритм построения сечения многоугольника плоскостью:

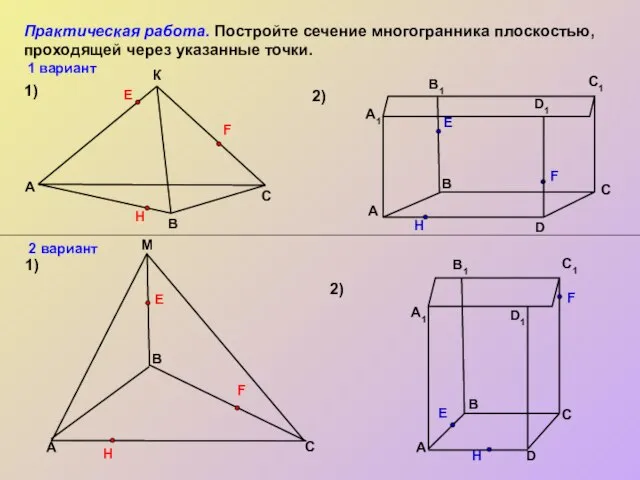
Практическая работа. Постройте сечение многогранника плоскостью, проходящей через указанные точки.
M
A
А1
1)
1)
2)
2)
В
С
К
В
A
С
A
D
C
B
A
В
С
D
B1
С1
D1
C1
B1
A1
D1
E
F
H
E
H
F
H
E
F
F
H
E
1 вариант
2 вариант

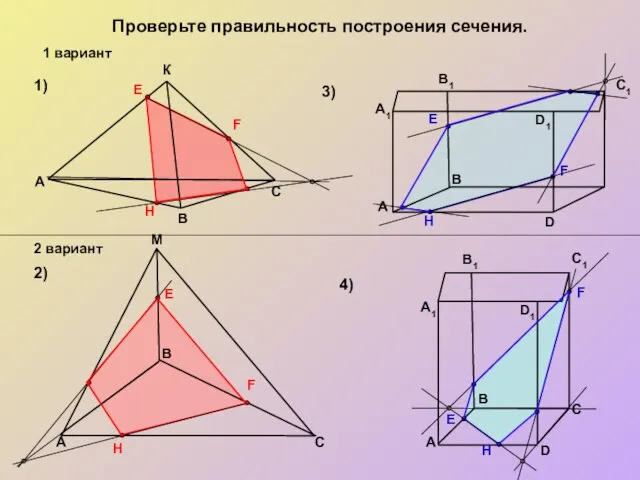
Проверьте правильность построения сечения.
M
A
А1
1)
2)
3)
4)
В
С
К
В
A
С
A
D
C
B
A
В
D
B1
С1
D1
C1
B1
A1
D1
E
F
H
E
H
F
H
E
F
F
H
E
1 вариант
2 вариант

Домашнее задание:
§
4. п.14. учебника
1.
2. № 72, №82(а,б), № 83(б).