Построение уточненной теории пластин с применением уравнения равновесия элементарного столбика Выполнил: Скращук Дми
Содержание
- 2. Элементарный столбик Постановка задачи Решение задачи Результаты Выводы
- 3. Элементарный столбик Уравнение равновесия элементарного столбика (1) (1)
- 4. Постановка задачи Дана круглая толстая плита нагруженная параболической нагрузкой, края которой находятся в абсолютно жёстких вертикальных
- 5. Решение задачи Для решения поставленной задачи используем уравнение равновесия элементарного столбика (1). Искомые перемещения представим в
- 6. Решение задачи Раскрывая вариационное уравнение (1) для разложений (2) и вариаций (3), после некоторых преобразований получим:
- 7. Решение задачи Их общие решения приведенные принимают вид:
- 8. Решение задачи Применяя метод неопределённых коэффициентов можно построить решения для Wi и нагрузок вида: Ui найдём
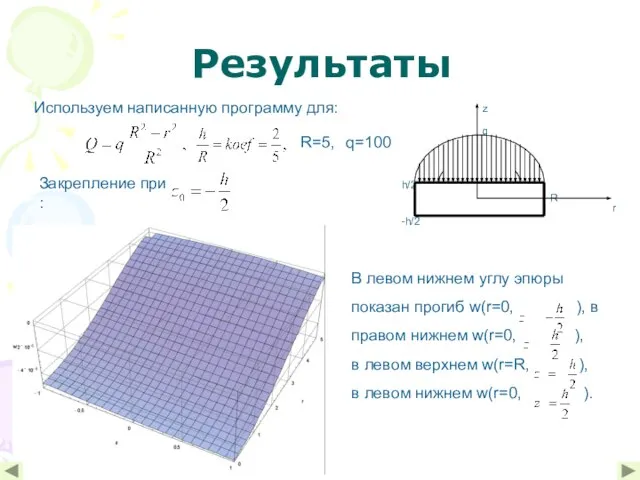
- 9. Результаты R=5, q=100 Используем написанную программу для: Закрепление при :
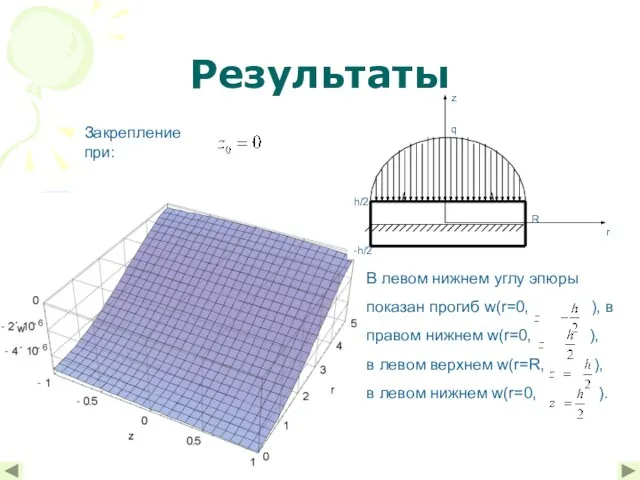
- 10. Результаты Закрепление при: :
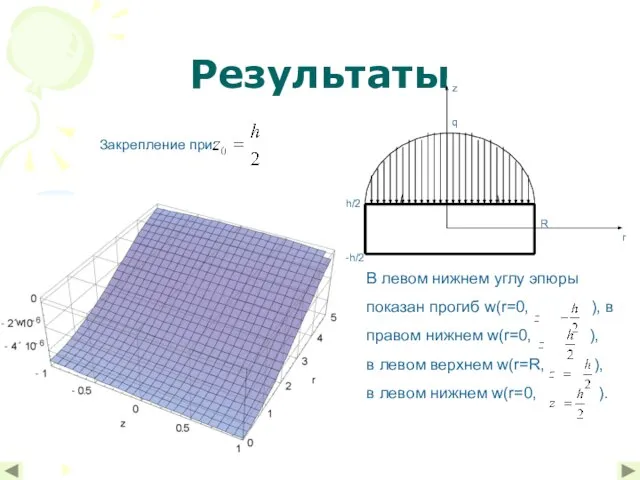
- 11. Результаты Закрепление при:
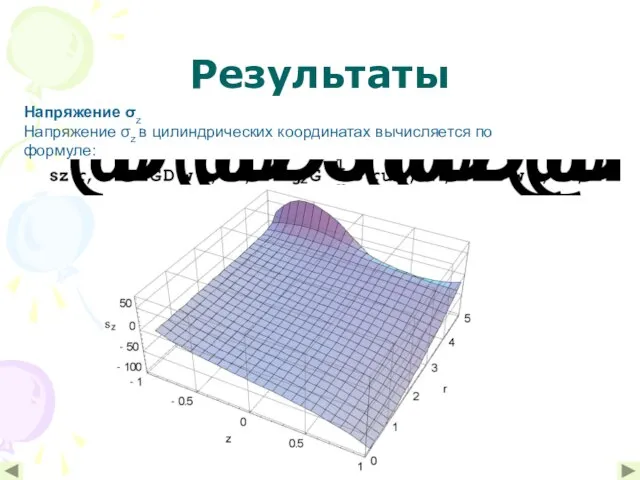
- 12. Результаты Напряжение σz Напряжение σz в цилиндрических координатах вычисляется по формуле:
- 13. Результаты Напряжение τrz в цилиндрических координатах вычисляется по формуле: τrz [r, z]=G( D[u[r, z], z]+ D[w[r,
- 14. Выводы Основными новыми результатами работы являются: 1. Разработана программа для нахождения вертикального w и горизонтального u
- 16. Скачать презентацию







![Результаты Напряжение τrz в цилиндрических координатах вычисляется по формуле: τrz [r, z]=G(](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/439409/slide-12.jpg)

 Может каждый грамотей Собрать слово из частей
Может каждый грамотей Собрать слово из частей Пять строчек по правилам "СИНКВЕЙН"
Пять строчек по правилам "СИНКВЕЙН" Наша школа в реализации государственной программы развития системы образования города Москвы на период 2012-2016 годы
Наша школа в реализации государственной программы развития системы образования города Москвы на период 2012-2016 годы Дорожная карта внедрения бизнес - процессов
Дорожная карта внедрения бизнес - процессов Комплексные решения (1) (1)
Комплексные решения (1) (1) Праздники февраля
Праздники февраля Замысел архитектурного проекта и его осуществление
Замысел архитектурного проекта и его осуществление Сборы на базе спортивного кластера Кировец-Восхождение
Сборы на базе спортивного кластера Кировец-Восхождение Урок бабочки
Урок бабочки Масштабирование, резервируемость, диагностика, репликация и резервное хранение данных
Масштабирование, резервируемость, диагностика, репликация и резервное хранение данных Ф.А. Васильев. Мокрый луг
Ф.А. Васильев. Мокрый луг Digital payment gateway
Digital payment gateway УМК под редакцией Б.М. Неменского ИЗО
УМК под редакцией Б.М. Неменского ИЗО Математика в древних странах
Математика в древних странах Анализ заданий ЕГЭ
Анализ заданий ЕГЭ Сэкономьте свое время, оформите заказ с получением в МОБИЛЬНОМ ПУНКТЕ ВЫДАЧИ 1. Разместите заказ: На сайте www.oriflame.ru По телефонам 39-
Сэкономьте свое время, оформите заказ с получением в МОБИЛЬНОМ ПУНКТЕ ВЫДАЧИ 1. Разместите заказ: На сайте www.oriflame.ru По телефонам 39- Применение тригонометрии в жизни
Применение тригонометрии в жизни Операционная система компьютера
Операционная система компьютера Лутовинов_презентация
Лутовинов_презентация 7840fc6f2793659aec37bad987934ba7073b57be-1664610122974
7840fc6f2793659aec37bad987934ba7073b57be-1664610122974 ГРУППА КОМПАНИЙ «ДЖЕНСЕР» ВЕКСЕЛЬНАЯ ПРОГРАММА Информационный меморандум ОРГАНИЗАТОР, АНДЕРРАЙТЕР И ПЛАТЕЖНЫЙ АГЕНТ КБ «ЛОКО-Б
ГРУППА КОМПАНИЙ «ДЖЕНСЕР» ВЕКСЕЛЬНАЯ ПРОГРАММА Информационный меморандум ОРГАНИЗАТОР, АНДЕРРАЙТЕР И ПЛАТЕЖНЫЙ АГЕНТ КБ «ЛОКО-Б Противовоздушная оборона
Противовоздушная оборона Как стать самостоятельным (складывание индивидуальной образовательной траектории)
Как стать самостоятельным (складывание индивидуальной образовательной траектории) The history of the brand Mini
The history of the brand Mini Н.М. Рубцов Ночь на Родине
Н.М. Рубцов Ночь на Родине Асоциация безопасноти бизнеса Латвий
Асоциация безопасноти бизнеса Латвий Презентация на тему Гигиена зрения
Презентация на тему Гигиена зрения  «Роль и место математического моделирования в прикладных исследованиях»
«Роль и место математического моделирования в прикладных исследованиях»