Содержание
- 2. 1. Типы потоков платежей Потоки платежей – это платежи, последовательные во времени (выплаты, по купонам облигаций,
- 3. Регулярный поток платежей (финансовая рента, аннуитет) – это платежи, у которых все выплаты направлены в одну
- 4. Наращенная сумма потока платежей – это сумма всех выплат с начисленными на них к концу срока
- 5. Рассмотрим общий случай потока платежей Введем обозначения:
- 6. (2.1) – наращенная сумма (2.2) – современная стоимость потока платежей
- 7. Формулу (2.2) можно получить иначе (дисконтированием наращенной суммы (2.1)) (2.3) – современная стоимость потока платежей
- 9. Решение: 1. Наращенная сумма по (2.1): 2. Современная стоимость потока платежей по (2.2): 3. Современная стоимость
- 10. 2. Финансовые ренты По моменту выплат в пределах между началом и концом периода ренты делятся на:
- 11. Рассмотрим финансовые ренты постнумерандо Постоянной называется рента, выплаты которой не изменяются во времени Годовая рента постнумерандо
- 12. Определим наращенную сумму годовой ренты. В течение n лет в фонд (банк) в конце каждого года
- 13. Формулу (2.4) можно переписать в виде: (2.5) (2.6) – коэффициент наращения ренты (табулированная функция)
- 14. Для определения современной стоимости годовой ренты проведем дисконтирование каждого платежа на начало срока ренты и найдем
- 15. (2.7) – современная стоимость годовой ренты Формулу (2.7) можно переписать в виде: (2.8) (2.9) - коэффициент
- 17. Наиболее общий тип ренты с начислением процентов по номинальной процентной ставке и неоднократными выплатами в году
- 18. Если выплаты производятся p раз в году, то такая рента называется p-срочной, или рентой с неоднократными
- 19. (2.11) - коэффициент наращения p-срочной ренты (табулированная функция) (2.12) – современная стоимость p-срочной ренты (2.13) –
- 22. Частный случай: количество начислений процентов в году равно количеству выплат в году (m=p) (2.10)-(2.13)⇒ (2.14) -
- 25. Рассмотрим случай годовой ренты с начислением процентов по номинальной процентной ставке (p=1). (2.10)-(2.13)⇒ (2.16) - наращенная
- 26. (2.18) – современная стоимость ренты (2.19) – коэффициент приведения ренты (табулированная функция)
- 29. Рассмотрим p-срочную ренту (m=1) (2.10)-(2.13)⇒ (2.20) - наращенная сумма (2.21) – коэффициент наращения ренты (табулированная функция)
- 30. (2.22) – современная стоимость ренты (2.23) – коэффициент приведения ренты (табулированная функция)
- 32. Финансовые ренты пренумерандо и ренты с выплатами в середине периодов Расчеты характеристик аналогичны рентам постнумерандо (2.24)
- 33. А1, А - современная стоимость ренты пренумерандо и постнумерандо с начислением процентов по номинальной процентной ставке
- 36. Рассмотрим ренту с выплатами в середине периода: S1/2 - наращенная сумма ренты c выплатами в середине
- 37. (2.27) - современная стоимость ренты c выплатами в середине периода А1/2 - современная стоимость ренты c
- 40. Финансовые отложенные и вечные ренты Отложенными называются ренты, у которых начало выплат отложено вперед Порядок вычислений:
- 41. (2.28) - современная стоимость годовой отложенной ренты А - современная стоимость исходной ренты, у которой моментом
- 43. Задача деления ренты постнумерандо между двумя участниками Годовая выплата R, срок n. Вначале выплаты получает первый
- 44. Из условия ⇒ ⇒ С учетом n2=n-n1, n1=t ⇒
- 45. Прологарифмируем (2.30)⇒ ⇒ (2.31) - время получения доли первым участником Если срок ренты очень большой или
- 46. (2.12) (2.13) ⇒ (2.31) – современная стоимость p-срочной ренты с начислением процентов несколько раз в году
- 50. Финансовые ренты с непрерывным начислением процентов (2.1) (2.2) m→∝ ⇒ (2.34) – наращенная сумма (2.35) –
- 51. Частный случай: годовая рента (p=1) (2.36) – наращенная сумма (2.37) – коэффициент наращения ренты
- 53. (2.12), (2.13), m→∝: (2.38) (2.39) - современная стоимость p-срочной ренты с непрерывным начислением процентов
- 54. Частный случай: годовая рента (p=1) (2.40) – современная стоимость (2.41) – коэффициент приведения ренты Связь между
- 56. Ренты с непрерывной выплатой платежей (p→∝) (2.42) - коэффициент наращения ренты (2.43) - коэффициент приведения ренты
- 57. (2.34) – наращенная сумма (2.45) – современная стоимость
- 59. 2.5. Финансовые ренты с ежегодными изменениями выплат на постоянную величину Переменной рентой называется поток платежей, у
- 60. Окончательно получим: (2.46) – современная стоимость ренты (2.47) – связь современной стоимости ренты с наращенной суммой
- 63. 2.6. Финансовые ренты с изменением выплат по закону геометрической прогрессии Пусть выплаты в течение n лет
- 64. Если q=1+Δ, где Δ - темп прироста ренты, то (2.49) – совре- менная стоимость (2.50) –
- 65. Подставим (2.50) в (2.49): (2.51) – наращенная сумма
- 67. 3. Непрерывные потоки платежей, изменяющиеся во времени
- 68. Определим наращенную сумму для момента n при выплате в момент t: (2.52) - сила роста R(t)dt
- 69. (2.54) – современная стоимость непрерывного переменного потока платежей (2.55) (2.53), (2.54)⇒ (2.56) – связь между S
- 70. 3.1. Непрерывные потоки платежей, изменяющиеся по параболическому закону Поток платежей, изменяющийся по параболическому закону, представим в
- 71. (2.58) – наращенная сумма здесь
- 74. 3.2. Непрерывные потоки платежей, изменяющиеся по линейному закону Поток представим в виде: Rt=R(t)=R+at Подставим b=0 в
- 76. 4. Расчет параметров финансовой ренты Для p-срочной ренты с начислением процентов m раз в году величина
- 79. В практической деятельности актуальны задачи определения срока ренты (при прочих известных параметрах). Рассмотрим общий случай –
- 80. Найдем срок n. Для этого: 1) Представим (2.63) в виде: (2.64) 2) Прологарифмируем (2.64): (2.65)
- 81. 3) Решим (2.65) относительно n: (2.66) При расчете по (2.66) срок получается, как правило, дробным. Количество
- 84. Частный случай: начисление процентов по номинальной процентной ставке и неоднократными выплатами в году (2.68) – срок
- 86. Если известны все параметры ренты, кроме процентной ставки, то расчет процентной ставки можно трактовать как определение
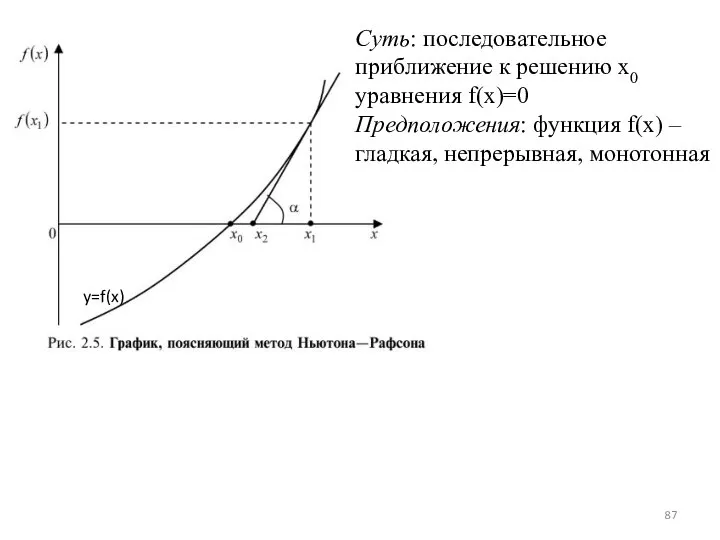
- 87. Суть: последовательное приближение к решению x0 уравнения f(x)=0 Предположения: функция f(x) – гладкая, непрерывная, монотонная y=f(x)
- 88. Алгоритм: 1) ввести x1- начальное приближение, ε - требуемая точность (например: 0,01; 0,001); 2) через т.
- 89. Из прямоугольного треугольника⇒ (2.69) (2.69)⇒ t – номер шага (итерации)
- 90. Для годовой ренты: (2.70) – современная стоимость Замена: x=1+i ⇒ тогда (2.70) ⇒ Искомая функция: Производная:
- 93. Аналогично проводятся расчеты для других типов рент. Например, для p-срочной ренты: - современная стоимость Искомая функция:
- 102. Скачать презентацию























































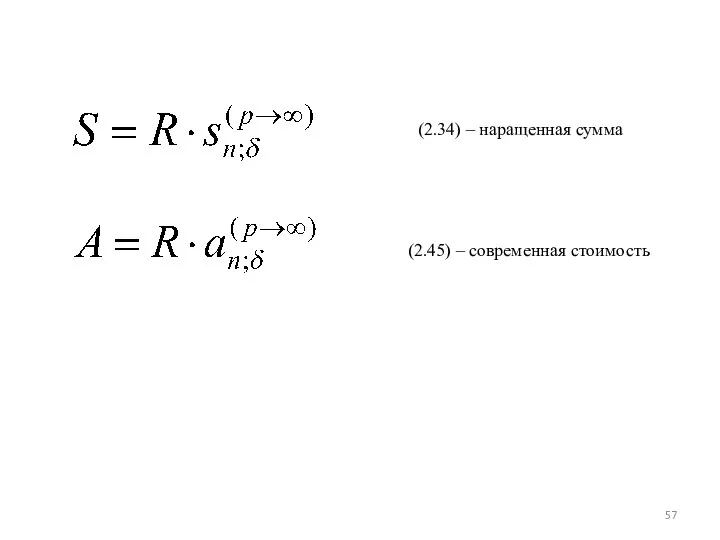











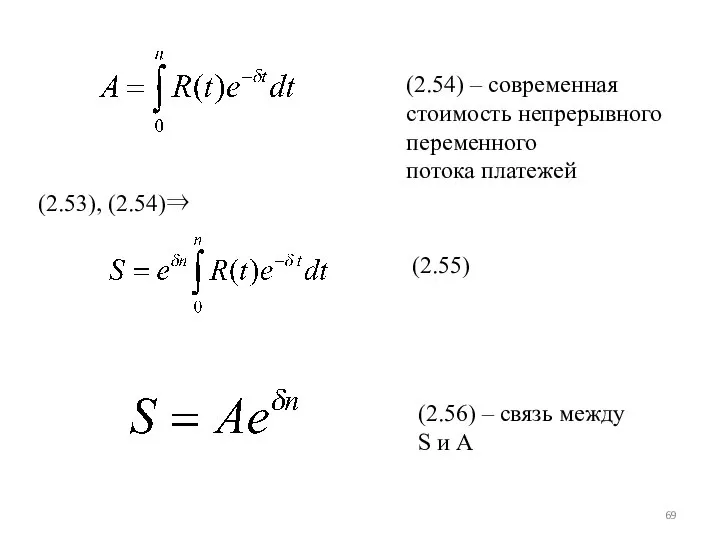






























 Размещение наружной рекламы
Размещение наружной рекламы эпиграф Легко любить Родину в дни ее величия и славы, но достоин уважения тот, кто служит ей в дни скорби и испытаний. Философ В.Роза
эпиграф Легко любить Родину в дни ее величия и славы, но достоин уважения тот, кто служит ей в дни скорби и испытаний. Философ В.Роза 41251
41251 Презентация на тему Осенние этюды
Презентация на тему Осенние этюды Interprété par Richard Verreau
Interprété par Richard Verreau Налоговые информационные системы
Налоговые информационные системы Памятка для выпускников
Памятка для выпускников Общественно-активная школа в контексте Национальной образовательной инициативы "Наша новая школа " А.К.Лукина Зав.кафедрой общей
Общественно-активная школа в контексте Национальной образовательной инициативы "Наша новая школа " А.К.Лукина Зав.кафедрой общей Что такое NAUKA 0+
Что такое NAUKA 0+ Ли́зинг. Схема лизинговой сделки
Ли́зинг. Схема лизинговой сделки Торгівельно-розважальний центр From overseas
Торгівельно-розважальний центр From overseas О знаках препинания
О знаках препинания Культура Византии
Культура Византии Работы художников, входящих в различные союзы
Работы художников, входящих в различные союзы Присяга і Положення про Бойовий Прапор
Присяга і Положення про Бойовий Прапор Презентация на тему Насекомые - переносчики возбудителей болезней и паразиты
Презентация на тему Насекомые - переносчики возбудителей болезней и паразиты Inventors and their inventions
Inventors and their inventions Департамент продаж
Департамент продаж Education system in china
Education system in china Методы актуализации и повышения качества данных о земельных участках и объектах недвижимости в целях увеличения сбора местных им
Методы актуализации и повышения качества данных о земельных участках и объектах недвижимости в целях увеличения сбора местных им 20141105_voronezh_segodnya
20141105_voronezh_segodnya Літаки і хвости
Літаки і хвости Использование вихревого эффекта в зерновой промышленности
Использование вихревого эффекта в зерновой промышленности Презентация на тему Виктор Цой
Презентация на тему Виктор Цой МикротурбинаMTI 250
МикротурбинаMTI 250 Кто такие птички
Кто такие птички  Центр образования,исследований и разработок «ИНО Томск’2020»
Центр образования,исследований и разработок «ИНО Томск’2020» Праздник победы.
Праздник победы.