Правила сложения и умножения вероятностей

- надежность
- система без резервирования
- система с резервированием
- вероятность хотя бы одного из событий
- правило сложения для совместных событий
- неравенство вероятностей
- формула Бернулли
- формула гипотез ( полной вероятности)
- формула Бейеса

Правило сложения для несовместных событий
Вероятность суммы двух несовместных событий (т.е., одного из них) равна сумме их вероятностей:
P(A + B) = P(A) + P(B), если A ⋅ B = ∅
Из аксиоматического определения:
(только для него − «как получено»)
Ω
B
Эта сумма равна сумме двух первых

По классическому определению :
пусть в эксперименте с равновозможными исходами mA элементарных событий благоприятны событию А, mB – событию B, (mA + mB) – событию (A + B).
Тогда:
P(A+B) = (mA + mB) / n = mA/n + mB/n = P(A) + P(B)
→ теорема доказана
Вероятность наступления одного из попарно несовместных событий
равна сумме
их вероятностей:
Обобщается на k несовместных событий (k > 2)

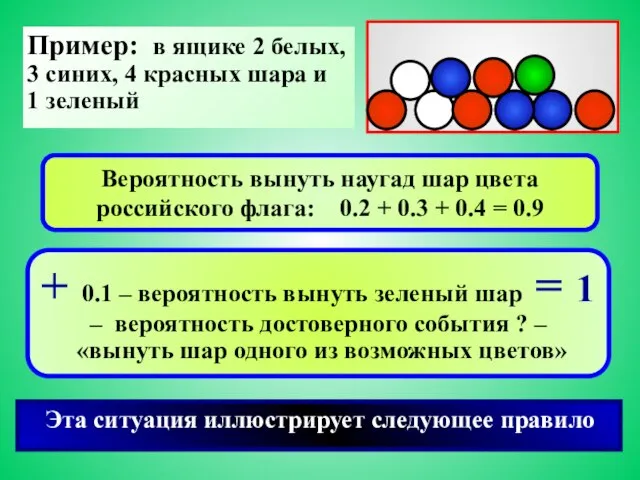
Пример: в ящике 2 белых, 3 синих, 4 красных шара и
1 зеленый
Вероятность вынуть наугад шар цвета российского флага: 0.2 + 0.3 + 0.4 = 0.9
+ 0.1 – вероятность вынуть зеленый шар = 1
– вероятность достоверного события ? –
«вынуть шар одного из возможных цветов»
Эта ситуация иллюстрирует следующее правило

Важный частный случай –
противоположные события
Сумма вероятностей противоположных событий равна единице
P( A ) + P(A ) = 1
p
q

Часто на практике оценивается вероятность отказа объекта q, а затем определяется надежность p
(вероятность безотказной работы)
p = 1 − q
Зависимые и независимые события. Условная и безусловная вероятность
Два события называют независимыми, если наступление одного из них не изменяет вероятности другого

Пример
Эксперимент: из коробки с 5 белыми и 3 черными шарами извлекаются наугад 2 шара.
События: В – 1-ый шар черный, А – 2-ой шар белый.
2 разные схемы эксперимента:
а) «схема с возвращением»
(1-ый шар возвращается перед доставанием 2-го);
б) «схема без возвращения» (1-ый шар не возвращается)
Вероятности:
а) P(А) = 5 / 8 (не зависит от того, было ли В)
P(В) = 3 / 8 → А и В – независимые
б) P(А) = 4 / 7, если В не произошло, но
P(А) = 5 / 7, если В произошло
→ вероятность наступления А
зависит от наступления или не наступления В

Условная вероятность − P(A/B) или PB(A)
есть вероятность события А, вычисленная при условии, что событие В имело место.
Вероятность независимого события – безусловная
(абсолютная)
Как следует из определений вероятности,
условная вероятность равна вероятности совместного наступления двух событий, деленной на вероятность события, о котором предполагается, что оно имело место:
P(A/B) = P(A⋅B) / P(B)
Отсюда cледует
правило умножения вероятностей !

Правило умножения
Вероятность произведения двух событий
(т.е., их совместного наступления)
равна вероятности одного из них,
умноженной на условную вероятность другого
при условии, что первое имело место:
P(A⋅B) = P(B) ⋅ P(A/B)
P(A⋅B) = P(А) ⋅ P(В/А)
Пример. В эксперименте с шарами по схеме (б), когда 1-ый шар не возвращается, P(A⋅B) = (3/8)⋅(5/7) = 15/56 − вероятность того, что 1-ый черный, а 2-ой белый

Для независимых событий выполняется
(по определению) условие независимости:
P(A/B) = P(А), P(В/А) = P(B)
В этом случае правило умножения принимает следующую форму
P(A⋅B) = P(А) ⋅ P(В)
Вероятность произведения двух независимых событий равна произведению их вероятностей
Пример. В ситуации с возвращением шара (а)
P(A⋅B) = (5/8)⋅(3/8) = 15/64

Правило умножения обобщается на любое число взаимонезависимых событий
Вероятность совместного наступления независимых событий равна
произведению их вероятностей:
P(А1A2… Аk) = P(А1) ⋅ P(А2) ⋅ … ⋅ P(Аk)
Все последующие формулы для расчета вероятностей событий можно рассматривать как следствия правил сложения и умножения

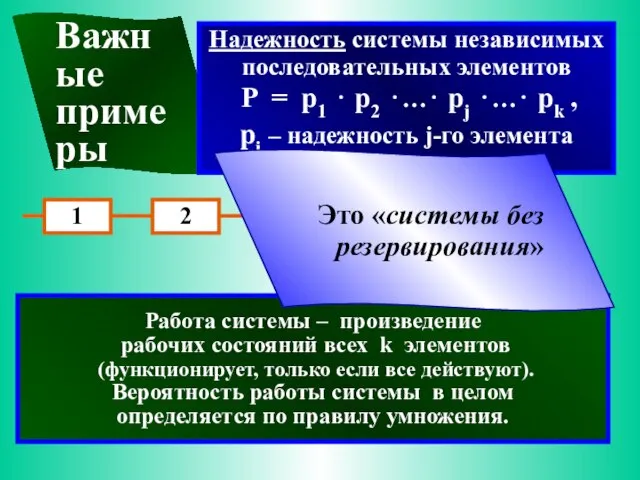
Важные примеры
Работа системы – произведение
рабочих состояний всех k элементов
(функционирует, только если все действуют). Вероятность работы системы в целом
определяется по правилу умножения.
Надежность системы независимых последовательных элементов
P = p1 ⋅ p2 ⋅…⋅ pj ⋅…⋅ pk ,
pj – надежность j-го элемента
Это «системы без резервирования»

Если надежность элементов одинакова, т.е.,
pj = p, j = 1…k → P = pk
Надежность системы без резервирования
падает с ростом количества элементов
Вероятность отказа такой системы:
Q = 1 – P = 1 – p1 p2…pj…pk

Отказ системы независимых элементов, работающих параллельно – произведение отказов элементов.
Откажет, только когда откажут все элементы.
Это « система с резервированием »
Вероятность отказа
Q = q1q2…qj…qk
Q = qk , если qj = q ( j = 1…k )
P = 1 – Q = 1 – q1 q2…qj…qk
Надежность системы с резервированием
растет с ростом количества элементов

В практических расчетах надежности
и вероятности отказа
наиболее удобно определить:
1) для последовательной системы – сначала P потом Q
2) для параллельной системы –
сначала Q затем P
NB!

Пример:
Вероятности отказа элементов системы q1 = 0.1, q2 = 0.2
1) Если элементы последовательны,
то надежность P = p1⋅ p2 = (1 – q1)⋅(1 – q2)
= 0.9 ⋅ 0.8 = 0.72;
вероятность отказа Q = 1 – P = 0.28
2) Если элементы действуют параллельно,
то Q = q1 ⋅ q2 = 0.1⋅0.2 = 0.02;
надежность P = 1 – Q = 1 – 0.02 = 0.98
Q ← «откажет хотя бы 1»
P ← «работает хотя бы 1»

Вероятность наступления хотя бы одного
из нескольких независимых событий равна единице без произведения вероятностей противоположных событий:
P(A = A1 + A2 + … + Ak)
= 1– p(Ā1)⋅p(Ā2)⋅ … ⋅p(Āk)
Общее правило для расчета вероятности
«хотя бы одного из событий»
(как совместных, так и не совместных)

Если событий лишь два, то вероятность
«по крайней мере одного» можно определить по правилу сложения для совместных событий
(при k > 2 существенно усложняется)
Вероятность наступления хотя бы одного
из двух совместных событий
равна сумме их вероятностей
без вероятности их совместного наступления:
P(A + B) = P(A) + P(B) – P(A⋅B)