Правило сложения для совместных А и В

Формула Бернулли
от «хотя бы 1»
к «ровно 1, ровно 2, ...»
Позволяет определять вероятности «ровно одного», «ровно двух» и т.д. наступлений события в нескольких независимых экспериментах
(попаданий при выстрелах, успехов в сделках и др.)
Если событие А может произойти в каждом
из n независимых опытов с вероятностью p,
то вероятность его наступления ровно k раз
в данной серии опытов
выражается формулой Бернулли:
Пояснение →

Cледует из правил умножения и сложения вероятностей:
вероятность, что А наступит
в некоторых k опытах и не наступит
в n-k остальных равна pkqn-k − по правилу умножения для независимых событий;
по правилу сложения Pn(k) равна сумме
таких вероятностей для всех вариантов
k наступлений и n-k не наступлений А;
количество таких вариантов есть число сочетаний из n элементов по k, т.е., Сnk

В серии из 3-х независимых выстрелов
с вероятностью попадания в каждом 0.7:
Пример
вероятность только одного попадания P3(1) = C31 ⋅ 0.7 ⋅ 0.32 = 0.189,
вероятность ровно двух попаданий
P3(2) = C32 ⋅ 0.72 ⋅ 0.3 = 0.441

Формула полной вероятности
и формула Байеса
связаны с ситуациями,
в которых эксперимент
как бы состоит из 2-х стадий:
на 1-ой «разыгрываются»
взаимоисключающие условия,
на 2-ой – определяется исход, когда имеет место одно из условий

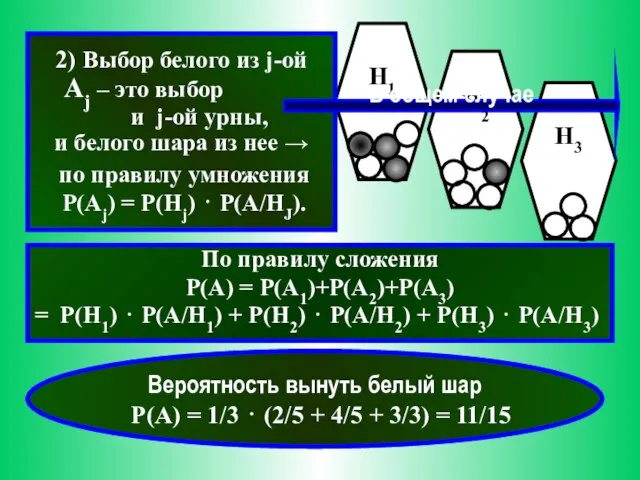
Пример. Имеются 3 урны
с белыми и черными шарами.
Шар можно вынуть случайным образом
из одной из них.
Какова вероятность того,
что извлеченный наугад шар белый,
если
в 1-ой урне 2 белых и 3 черных шара,
во 2-ой 4 белых и 1 черный,
в 3-ей – 3 белых шара?

1) Выбор урны (условий) – это
гипотеза Hj ,
что шар берется из j-ой урны
(hypothesis, предположение).
События H1, H2, H3 образуют полную группу:
они несовместны (альтернативны),
одно из них обязательно произойдет →
H1 + H2 + H3 = Ω,
P(H1) + P(H2) + P(H3) = 1.
Выбор случайный →
P(H1) = P(H2) = P(H3) = 1/3

1) Выбор урны (условий) – это гипотеза Hj
что шар берется из j-ой урны
(hypothesis, предположение).
События H1, H2, H3 образуют полную группу:
они несовместны (альтернативны),
одно из них обязательно произойдет →
H1 + H2 + H3 = Ω,
P(H1) + P(H2) + P(H3) = 1.
Выбор случайный →
P(H1) = P(H2) = P(H3) = 1/3

Вероятность вынуть белый шар
P(A) = 1/3 ⋅ (2/5 + 4/5 + 3/3) = 11/15
2) Выбор белого из j-ой
Аj – это выбор
и j-ой урны,
и белого шара из нее →
по правилу умножения
P(Aj) = P(Hj) ⋅ P(A/HJ).
По правилу сложения
P(A) = P(A1)+P(A2)+P(A3)
= P(H1) ⋅ P(A/H1) + P(H2) ⋅ P(A/H2) + P(H3) ⋅ P(A/H3)
В общем случае

Абсолютная, безусловная вероятность события
в эксперименте с гипотетическими условиями
рассчитывается как сумма произведений
вероятностей гипотез на условную вероятность
события при соответствующей гипотезе
Если об условиях эксперимента можно сделать
k исключающих друг друга предположений – гипотез H1 , H2 , …, Hk , и событие А
может иметь место при одной из этих гипотез,
то вероятность события А определяется
по формуле полной вероятности:

Нормальный режим работы устройства наблюдается в 80% случаев,
в 20% – режим аномальный.
Пример
Вероятность отказа устройства (А)
в 1-ом режиме 0.1, во 2-ом – 0.7
Безусловная вероятность отказа,
независимо от того,
в каком режиме он произошел:
P(A) = 0.8⋅0.1+ 0.2⋅0.7 = 0.22
Где гипотезы, где условные вероятности?

В условиях предыдущей задачи
пусть событие имело место – устройство прекратило работу. Какова вероятность,
что отказ произошел в нормальном режиме?
Для ответа на подобные вопросы используется формула Байеса
(для вероятностей гипотез)
P(Hj / A) =
Доля, шансы гипотезы в наступлении А

Пусть А может произойти при наступлении одного из событий, образующих полную группу − при гипотезах H1 , H2 , …, Hk
В общем случае
?
Какова вероятность случайно встретить в дверях длинноволосую студентку, если у 15 из 40 студенток в аудитории короткая стрижка?
Если до опыта вероятности гипотез были
P(H1), P(H2), …, P(Hk),
а в результате опыта событие А произошло,
то «новые» условные вероятности гипотез рассчитываются по формуле Байеса