Содержание
- 2. Цели и задачи: Дать понятие правильных многогранников ( на основе определения многогранников). Доказать почему существует только
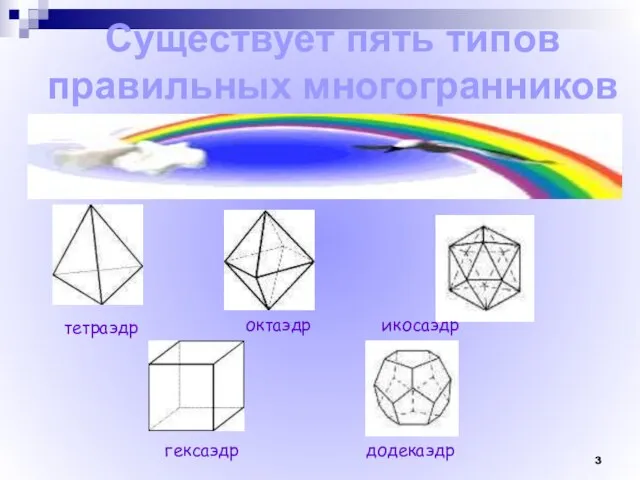
- 3. Существует пять типов правильных многогранников тетраэдр октаэдр икосаэдр гексаэдр додекаэдр
- 4. Определение многогранника: Многогранник – это часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединённых таким образом,
- 5. Правильным называется многогранник, у которого все грани являются правильными многоугольниками, и все многогранные углы при вершинах
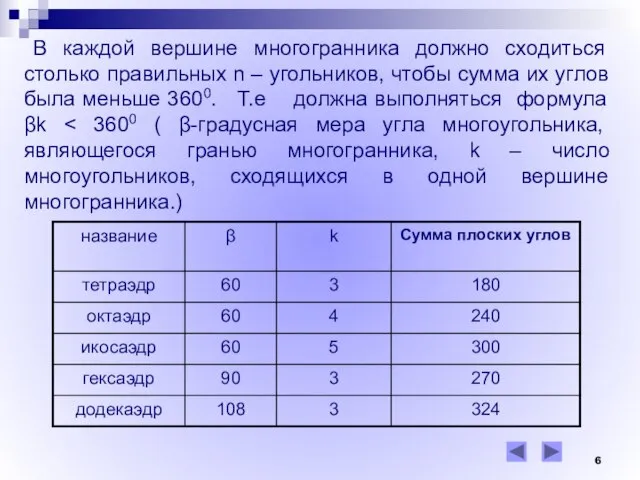
- 6. В каждой вершине многогранника должно сходиться столько правильных n – угольников, чтобы сумма их углов была
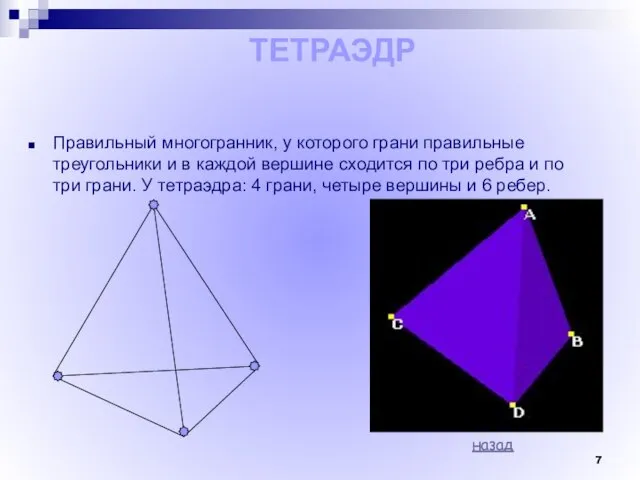
- 7. Правильный многогранник, у которого грани правильные треугольники и в каждой вершине сходится по три ребра и
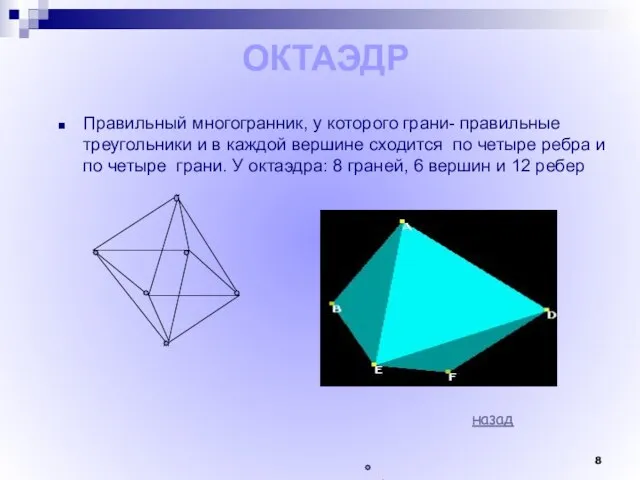
- 8. ОКТАЭДР Правильный многогранник, у которого грани- правильные треугольники и в каждой вершине сходится по четыре ребра
- 9. ИКОСОЭДР Правильный многогранник, у которого грани - правильные треугольники и в вершине сходится по пять рёбер
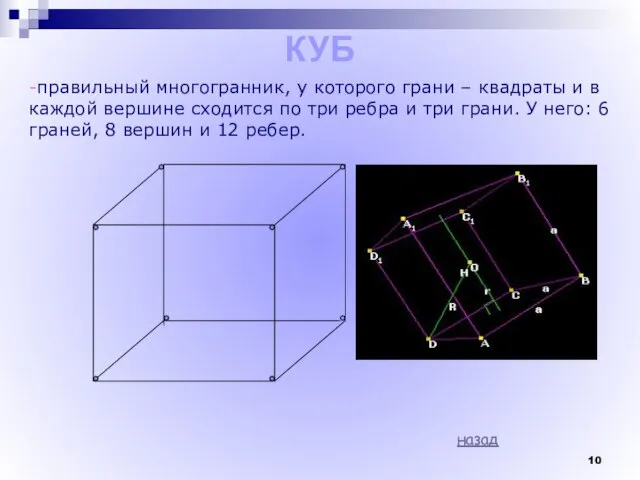
- 10. КУБ -правильный многогранник, у которого грани – квадраты и в каждой вершине сходится по три ребра
- 11. Додекаэдр Правильный многогранник, у которого грани правильные пятиугольники и в каждой вершине сходится по три ребра
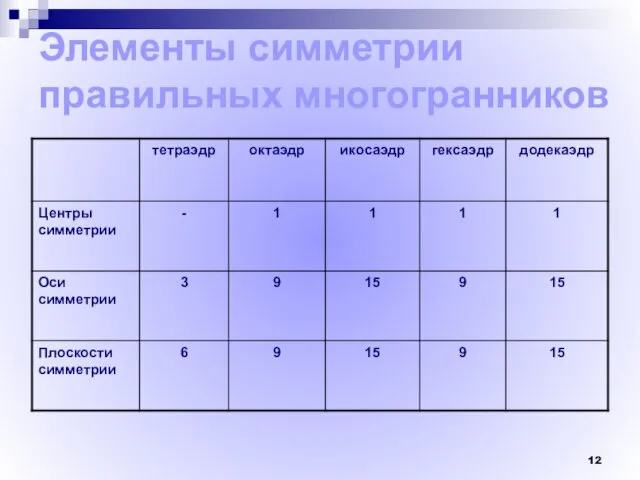
- 12. Элементы симметрии правильных многогранников
- 14. Немного истории Все типы правильных многогранников были известны в Древней Греции – именно им посвящена завершающая,
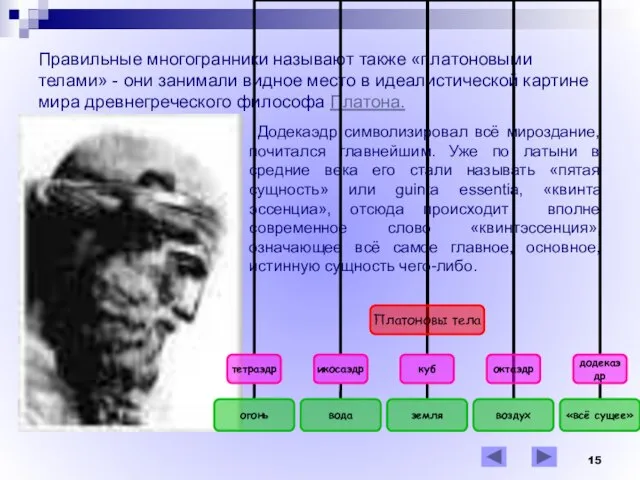
- 15. Правильные многогранники называют также «платоновыми телами» - они занимали видное место в идеалистической картине мира древнегреческого
- 16. Олицетворение многогранников.
- 17. Дюрер. Меланхолия
- 18. Тайна мировоззрения.
- 19. Выводы: Многогранник называется правильным, если: Он выпуклый; Все его грани равные правильные многоугольники; В каждой вершине
- 20. Евклид ЕВКЛИД, или ЭВКЛИД - древнегреческий математик, автор первых дошедших до нас теоретических трактатов по математике.
- 21. Платон Платон (Platon) (род. 427 - ум. 347 гг.до н.э.) - греческий философ. Родился в Афинах.
- 22. Определение правильного многоугольника Многоугольник называется правильным, если у него все стороны и все углы равны.
- 23. Построение с помощью куба
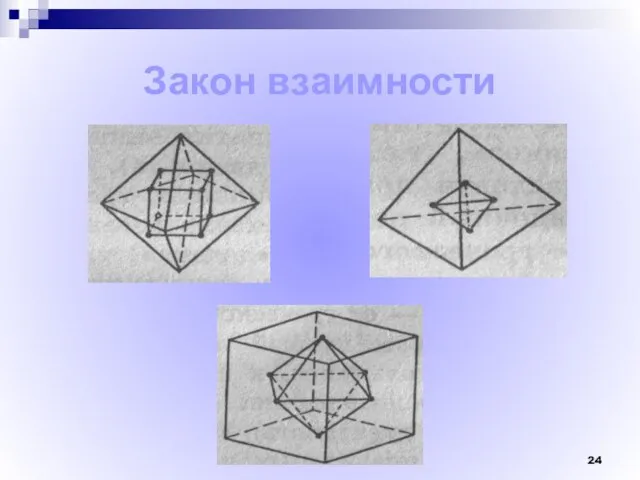
- 24. Закон взаимности
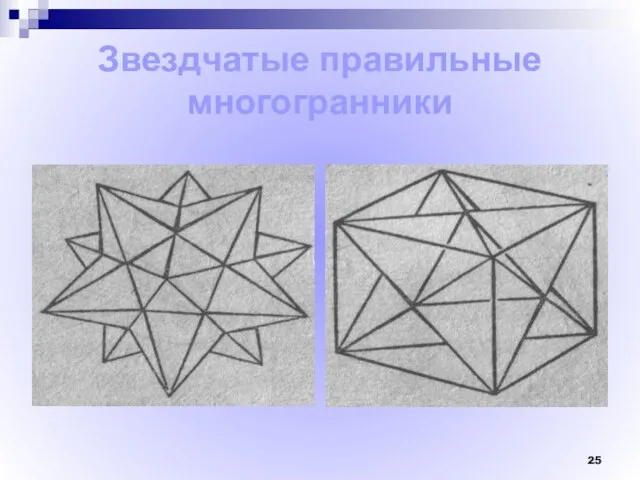
- 25. Звездчатые правильные многогранники
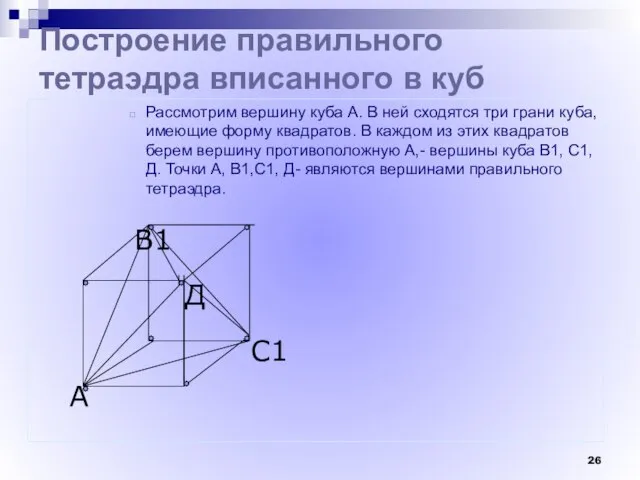
- 26. С1 В1 А Построение правильного тетраэдра вписанного в куб Рассмотрим вершину куба А. В ней сходятся
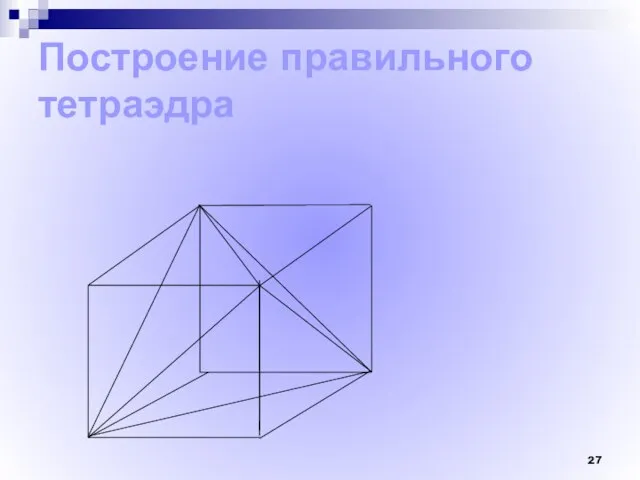
- 27. Построение правильного тетраэдра
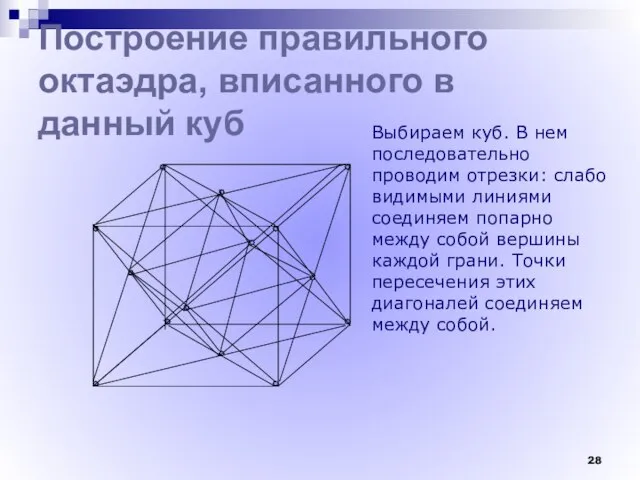
- 28. Построение правильного октаэдра, вписанного в данный куб Выбираем куб. В нем последовательно проводим отрезки: слабо видимыми
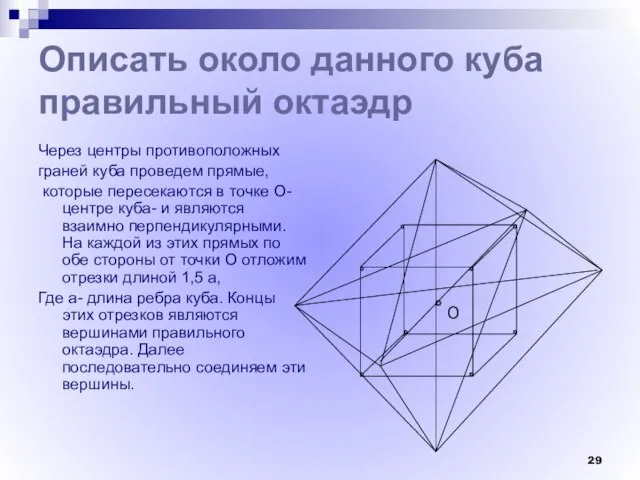
- 29. Описать около данного куба правильный октаэдр Через центры противоположных граней куба проведем прямые, которые пересекаются в
- 30. Построение икосаэдра, вписанного в куб Поместим на средних линиях граней куба по одному отрезку одинаковой длины
- 32. Скачать презентацию















 Аральское море
Аральское море Социальная психология
Социальная психология Педагогические Lookи
Педагогические Lookи Фізика754
Фізика754 Презентация на тему Равнодействующая сила
Презентация на тему Равнодействующая сила  Духовно – нравственные основы развития личности
Духовно – нравственные основы развития личности Мариинский театр. Владивосток
Мариинский театр. Владивосток Будни и праздники начальной школы
Будни и праздники начальной школы Каша во рту
Каша во рту Добро, ласка, поощрение, требовательность, твердость, ограничение желаний в воспитании детей
Добро, ласка, поощрение, требовательность, твердость, ограничение желаний в воспитании детей Жизнь прожить – не поле перейти, или «Этапы большого пути»
Жизнь прожить – не поле перейти, или «Этапы большого пути»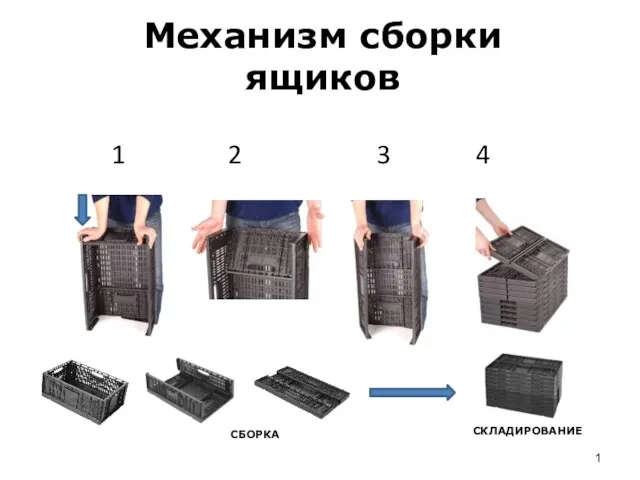 Механизм сборки ящиков
Механизм сборки ящиков « Распространение Реформации в Европе. Контрреформация»
« Распространение Реформации в Европе. Контрреформация» ПОЧЕМУ НУЖНО РАЦИОНАЛЬНО ИСПОЛЬЗОВАТЬ ЭНЕРГЕТИЧЕСКИЕ РЕСУРСЫ?
ПОЧЕМУ НУЖНО РАЦИОНАЛЬНО ИСПОЛЬЗОВАТЬ ЭНЕРГЕТИЧЕСКИЕ РЕСУРСЫ? Климат Тверской области
Климат Тверской области Мониторинг социальных настроений населения стран постсоветского пространства ЕМ-VI. Предварительные результаты 1 Проект «Евразий
Мониторинг социальных настроений населения стран постсоветского пространства ЕМ-VI. Предварительные результаты 1 Проект «Евразий Информационные компьютерные технологии в практике логопеда
Информационные компьютерные технологии в практике логопеда Презентация на тему путешествие Афанасия НИКИТИНА В ИНДИЮ 1466-1472
Презентация на тему путешествие Афанасия НИКИТИНА В ИНДИЮ 1466-1472  Конституция Российской Федерации
Конституция Российской Федерации Комедия А.С. Грибоедова «Горе от ума». Поэтика заглавия пьесы
Комедия А.С. Грибоедова «Горе от ума». Поэтика заглавия пьесы 1 Приоритетные направления стратегии развития области Модернизация власти, повышение ее конкурентоспособности Развитие человече
1 Приоритетные направления стратегии развития области Модернизация власти, повышение ее конкурентоспособности Развитие человече К. Паустовский Барсучий нос
К. Паустовский Барсучий нос Генетика человека
Генетика человека Maryinsky Park
Maryinsky Park Техническая эксплуатация и обслуживание электрического и электромеханического оборудования
Техническая эксплуатация и обслуживание электрического и электромеханического оборудования Из серии " 100 великих картин "
Из серии " 100 великих картин " Искусство эпохи. Возрождения Проторенессанс. Ранний Ренессанс
Искусство эпохи. Возрождения Проторенессанс. Ранний Ренессанс Простейший ремонт сантехнического оборудования
Простейший ремонт сантехнического оборудования